






НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра Систем Сбора и Обработки Данных
Дисциплина «Теория и обработка сигналов», 5 - й семестр
ЛАБОРАТОРНАЯ РАБОТА № 2
СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ
ПЕРИОДИЧЕСКИХ СИГНАЛОВ
Вариант № 3
Студент гр. АО-81
Васильева И.В.
Преподаватель
Доц. Щетинин Ю.И.
Новосибирск
2010
Цель работы:Изучение понятия спектра периодического сигнала, приобретение практических навыков вычисления, построения графиков и анализа спектров периодических сигналов в среде MATLAB.
Вариант задания № 3:
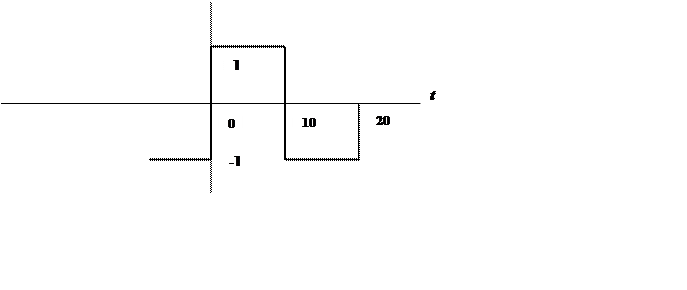
Рис.1. Вид сигнала
Ряд Фурье
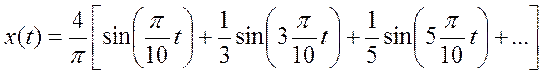
Ход работы:
1. Получение аналитически коэффициентов разложения ряда Фурье в комплексной форме.
Угловая
частота основной гармоники 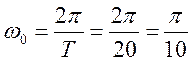
Коэффициенты комплексного ряда Фурье
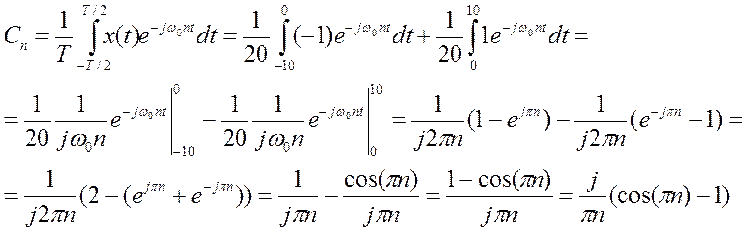
Ряд Фурье в комплексной форме выглядит так:
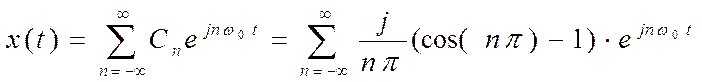
В частности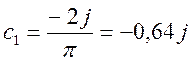 ;
; 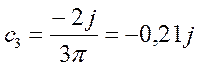 ;
;
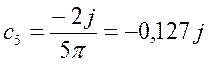
Чётные члены ряда равны нулю, т.к. данная функция является четной.
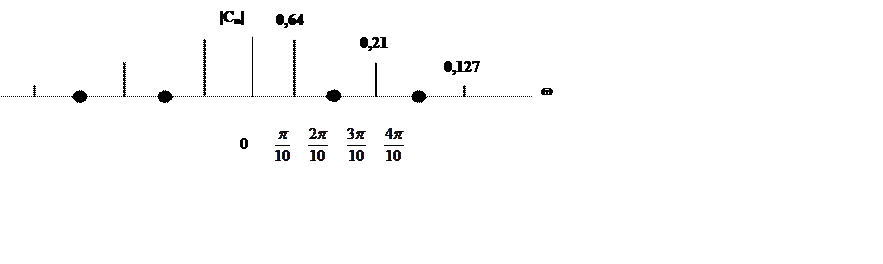
Рис.2. График амплитудного спектра сигнала
Из разложения в ряд Фурье сигнала прямоугольной формы следует, что гармонический ряд содержит только нечетные гармоники, при этом амплитуды гармоник убывают пропорционально номеру гармоники.[1]
2. Файл-сценарий (М-файл), позволяющий построить в Matlab графики амплитудного и фазового спектров сигнала на основе вычислений в п.1.
% Файл - сценарий для построения графиков спектров
n1=1:15; % положительные номера гармоник
cn=j./n1/pi.*(cos(n1*pi)-1); % реализация расчета коэффициента Фурье
n2=-15:-1;% отрицательные номера
c_n=j./n2/pi.*(cos(n2*pi)-1); %на разных интервалах
Cn=[c_n 0 cn];% коэффициенты Фурье для n>0, n=0, n<0
n3=[n2 0 n1];
n=-15:15;
figure(1);
subplot(2,1,1);
stem(n,abs(Cn)); %построение графика амплитудного спектра сигнала
title('|Cn|');
subplot(2,1,2);
stem(n,angle(Cn)); % построение графика фазового спектра сигнала
title('angle(c_n) in rad');
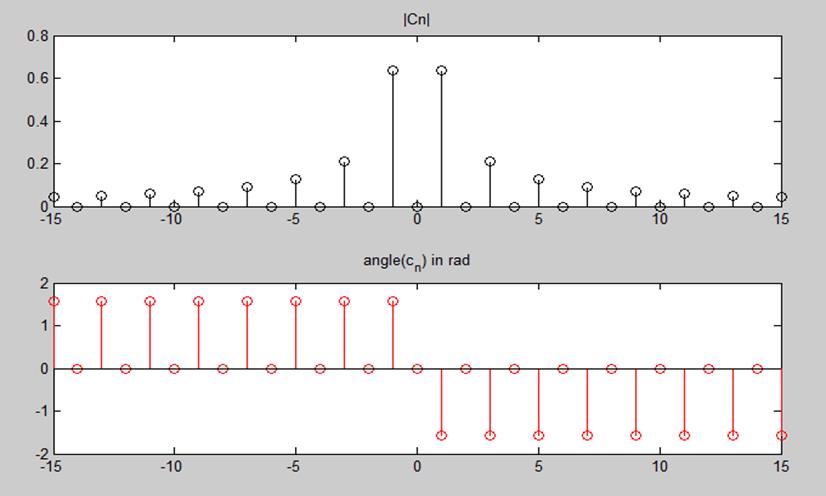
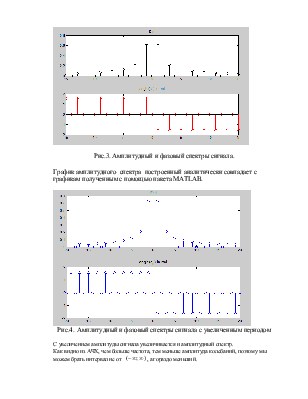
Рис.3. Амплитудный и фазовый спектры сигнала.
График амплитудного спектра построенный аналитически совпадает с графикам полученным с помощью пакета MATLAB.
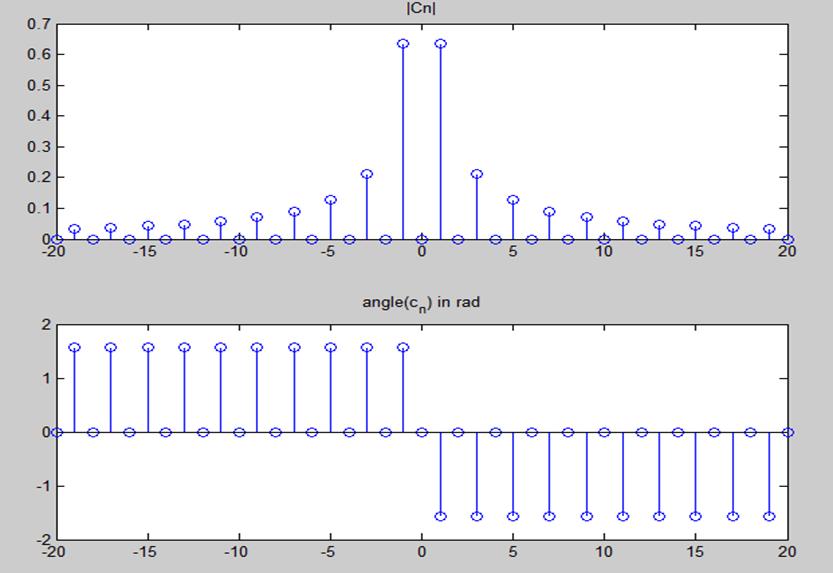
Рис.4. Амплитудный и фазовый спектры сигнала с увеличенным периодом
С увеличением амплитуды сигнала увеличивается и амплитудный спектр.
Как видно из АЧХ, чем больше частота, тем меньше амплитуда
колебаний, поэтому мы можем брать интервал не от ![]() ,
а гораздо меньший.
,
а гораздо меньший.
3. Определение спектра Фурье сигнала с помощью функции fft() Matlab.
T=20;% период сигнала
t=0:T/63:T;% временной интервал
x=1*rectpuls(t-5,10)-1*rectpuls(t-15,10);
% генерирование сигнала
figure(2);
% график сигнала
subplot(311), plot(t,x)
title(' График сигнала')
k=0:1:63;
% коэффициенты ряда Фурье
C=j/k/pi.*(cos(pi*k)-1);
% график амплитудного спектра
subplot(312),
stem(2*pi*k/T, abs(C));
title(' Амплитудный спектр сигнала')
y=fft(x,64);
% Дискретное преобразование Фурье сигнала
% график ДПФ
subplot(313), stem(2*pi*k/T, abs(y)/64)
xlabel(' Угловая частота, рад/сек')
title(' Амплитудный спектр сигнала по процедуре fft')
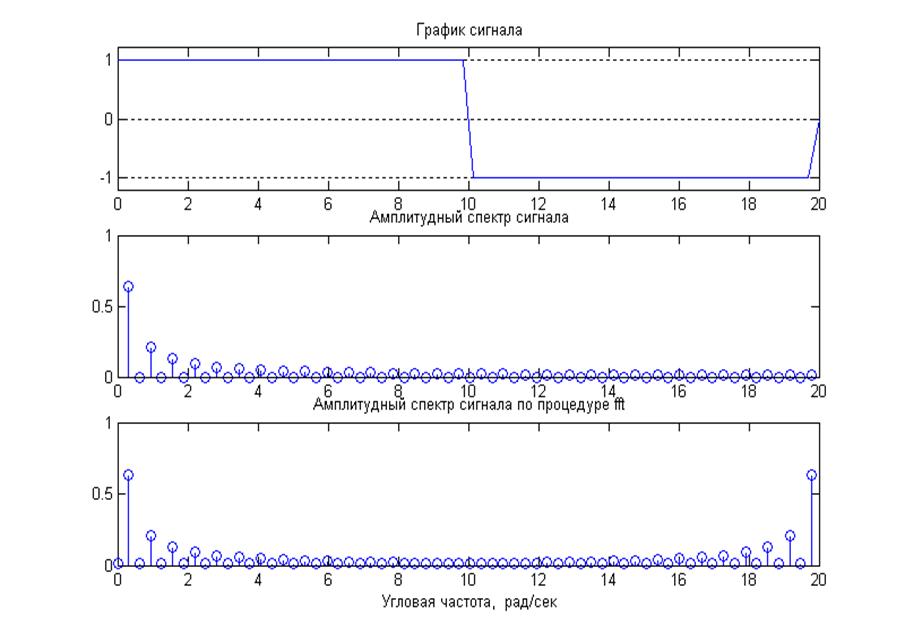
Рис.5. Изображен сверху вниз: исходный сигнал, амплитудный спектр сигнала(коэффициенты ряда Фурье найдены аналитически), амплитудный спектр сигнала с помощью процедуры fft.
fft(x) – вычисляет дискретное преобразование Фурье вектора x с помощью алгоритмов Быстрого Преобразования Фурье (БПФ). Характер периодичности спектра обусловлен тем что функции fft() вычисляет дискретное преобразование, а дискретный спектр периодичен.
4. Исследования сходимости ряда Фурье к исходному периодическому сигналу.
T=20;
w0 = 2*pi/T;
t = 0:T/1000:T;% интервал времени
% исходный сигнал
x1=1*rectpuls(t-5,10)-1*rectpuls(t-15,10);
N = input('Введите минимальное число членов ряда ');
N=N*8;
c0 = 0;
x = c0*ones(1,length(t)); % постоянная составляющая
for n=1:N,
cn =j./n/pi.*(cos(n*pi)-1);
c_n=conj(cn);
x = x + cn*exp(j*n*w0*t)+ c_n*exp(-j*n*w0*t);
end
figure(1), subplot(2,2,1), plot(t,x,t,x1, '--r'), grid
title(['N = ',num2str(N)]);
N=N/2;
x = c0*ones(1,length(t)); % постоянная составляющая
for n=1:N,
cn =j./n/pi.*(cos(n*pi)-1);
c_n=conj(cn);
x = x + cn*exp(j*n*w0*t)+ c_n*exp(-j*n*w0*t);
end
subplot(2,2,2), plot(t,x,t,x1, '--r'), grid
title(['N = ',num2str(N)]);
N=N/2;
x = c0*ones(1,length(t)); % постоянная составляющая
for n=1:N,
cn =j./n/pi.*(cos(n*pi)-1);
c_n=conj(cn);
x = x + cn*exp(j*n*w0*t)+ c_n*exp(-j*n*w0*t);
end
subplot(2,2,3), plot(t,x,t,x1, '--r'), grid
title(['N = ',num2str(N)]);
N=N/2;
x = c0*ones(1,length(t)); % постоянная составляющая
for n=1:N,
cn =j./n/pi.*(cos(n*pi)-1);
c_n=conj(cn);
x = x + cn*exp(j*n*w0*t)+ c_n*exp(-j*n*w0*t);
end
subplot(2,2,4), plot(t,x,t,x1, '--r'), grid
title(['N = ',num2str(N)]);
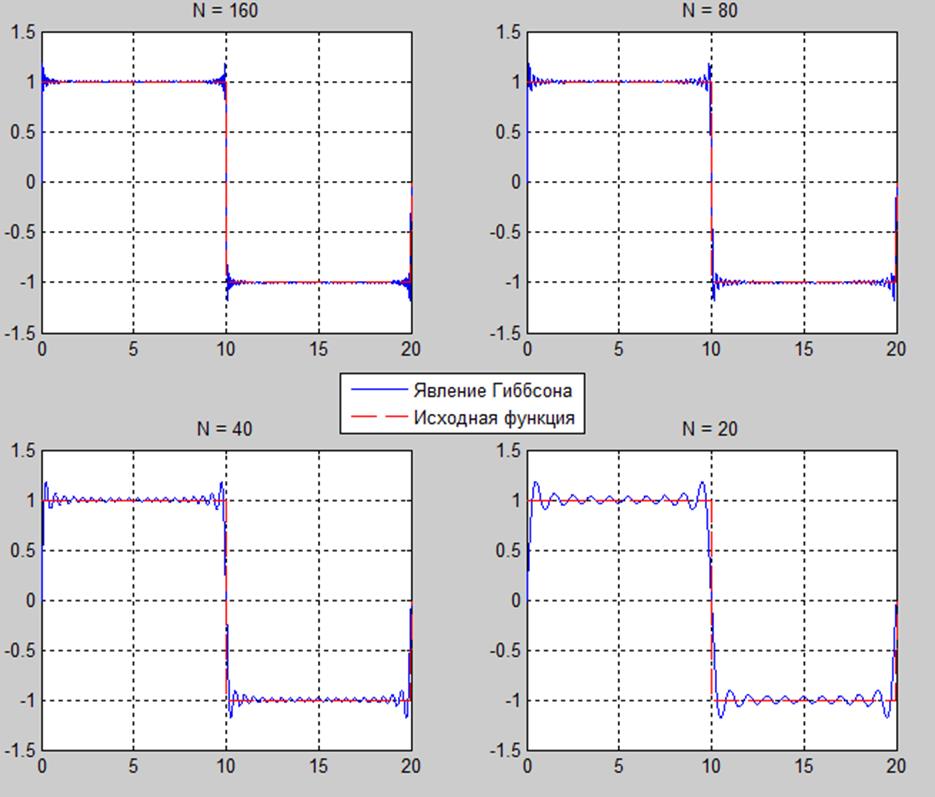
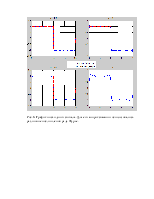
Рис.6. Графики исходного сигнала. Для его аппроксимации использовалось различное число членов ряда Фурье.
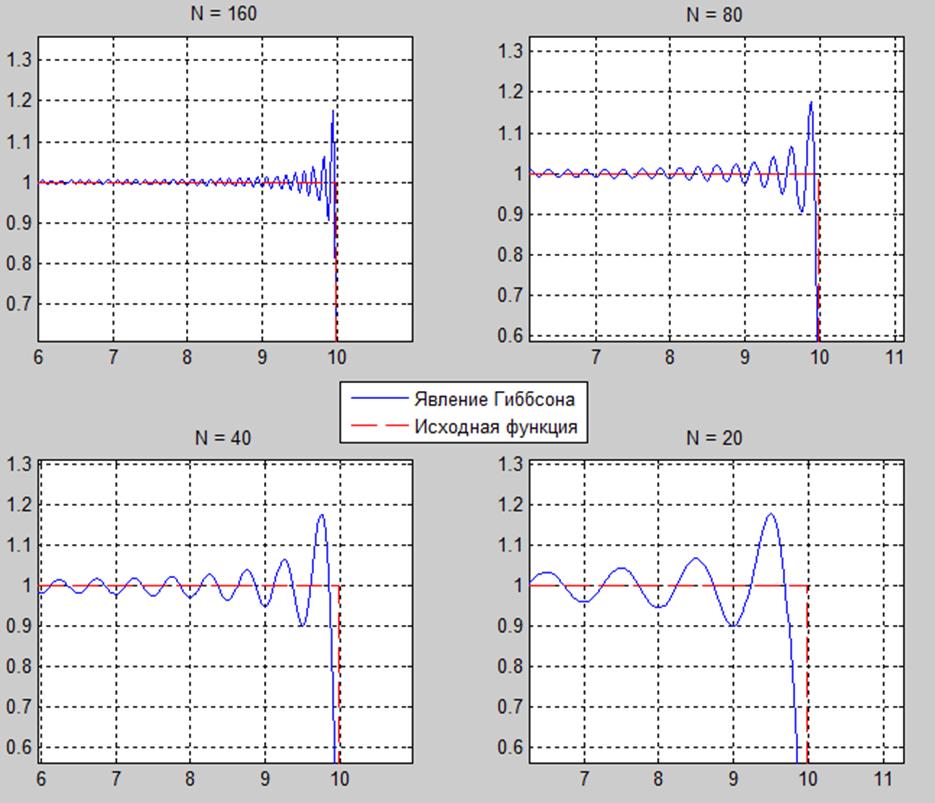
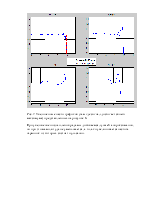
Рис.7. Увеличенные части графиков (там где сигнал достигает своего максимума) представленных на рисунке 6.
При увеличение числа членов ряда мы добиваемся лучшей аппроксимации, но при этом амплитуда не уменьшается, а только увеличивается частота гармоник из которых состоят пульсации.
Выводы:
1. Спектр периодического сигнала - это зависимость коэффициентов ряда Фурье от частоты гармоник, которым эти коэффициенты соответствуют.
2.
Любой конечный периодический
сигнал x(t), определенный для всех действительных t или
на конечном интервале времени ![]() , можно
представить рядом Фурье.
, можно
представить рядом Фурье.
3. Ряд Фурье в комплексной форме [2]
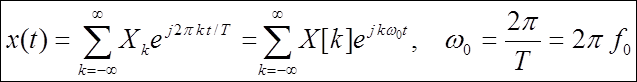
![]() - основная частота,
- основная частота,
![]() - основная угловая частота.
- основная угловая частота.
. 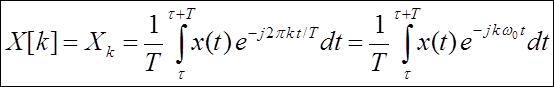
4. Процедура fft() вычисляет дискретное преобразование Фурье сигналов
по выражению 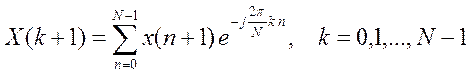 . От коэффициентов Фурье
дискретного периодического сигнала x[n] с периодом N
. От коэффициентов Фурье
дискретного периодического сигнала x[n] с периодом N
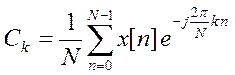 значения
X(k+1) отличаются
множителем
значения
X(k+1) отличаются
множителем ![]() и смещением индексов на 1,
так как индексация массивов в Matlab начинается
с 1.
и смещением индексов на 1,
так как индексация массивов в Matlab начинается
с 1.
5. Особенностью сходимости конечного ряда Фурье является среднеквадратический характер сходимости.
Среднеквадратическая сходимость означает, что
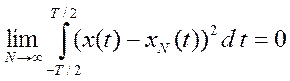 ,
,
т.е. при увеличении числа членов ряда N квадрат («энергия») разности между сигналом x(t) и его приближением xN(t) стремится к нулю.
Эта особенность сходимости носит название явления Гиббса.
Список литературы:
1. http://ets.ifmo.ru/osipov/os1/2_1.htm
2. Лекция №4 Лекционный курс «Теория и обработка сигналов», доц. Щетинин Ю.И., 2010 г.
3. Лекция №5 Лекционный курс «Теория и обработка сигналов», доц. Щетинин Ю.И., 2010 г.
4. Щетинин Ю.И. MATLAB в ТОС: Электронное уч. пособие. - Новосибирск. 2004.
5. Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов.: Уч. пособие.- Новосибирск. Изд-во НГТУ, 1998 - ч.2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.