Спектральные представления периодических сигналов. Вариант 1

            МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

НОВОСИБИРСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ 
УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ  ТЕХНИКИ

Кафедра  Систем Сбора и Обработки Данных

ЛАБОРАТОРНАЯ  РАБОТА  № 2

СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ

ПЕРИОДИЧЕСКИХ СИГНАЛОВ

Вариант 1

Группа:                                                                             Преподаватель:  Щетинин Ю.И.

Студент:

Новосибирск

 2009

Цель работы:  изучение понятия спектра  периодического сигнала, приобретение практических навыков вычисления,  построения  графиков и анализа спектров  периодических  сигналов в  среде MATLAB.

1.  Разложение периодического сигнала в ряд Фурье.

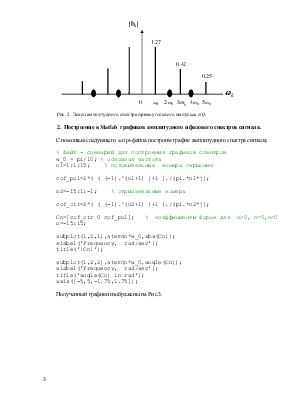
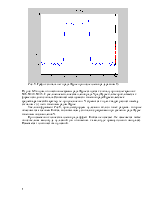
Сигнал задан графиком, представленным на Рис. 1.

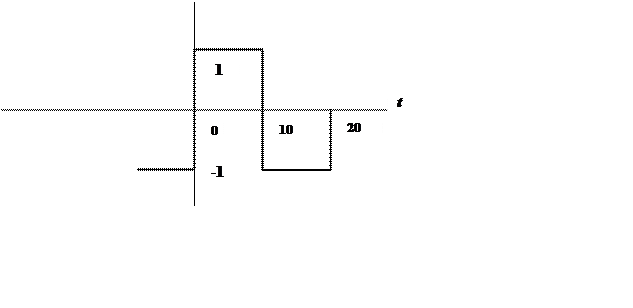
Рис. 1.  График сигнала.

Получим аналитически коэффициент разложения в комплексный ряд Фурье.

Функция периодическая с периодом T = 20 и угловой частотой .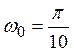

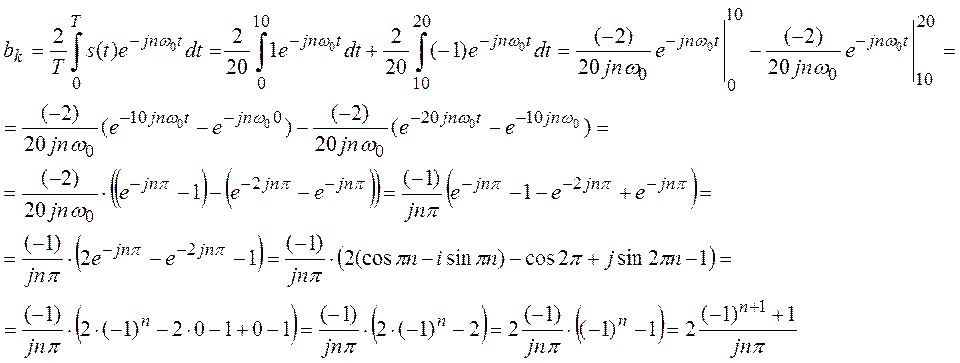
                                                                                                                                                 (1)

Построим ряд Фурье для данного сигнала.

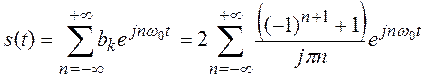                                                                          (2)                                                      

Амплитудный спектр сигнала можно найти, как:

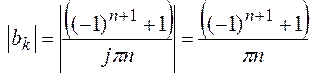                                                                                             (3)

Построим приближенный график амплитудного спектра  сигнала .

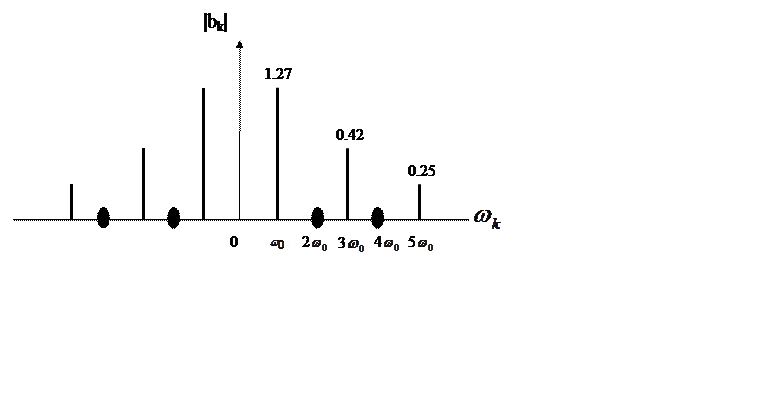
Рис. 2. Эскиз амплитудного спектра прямоугольного импульса s(t).

2.  Построение в Matlab  графиков амплитудного и фазового спектров сигнала.

С помощью следующего script-файла построим график амплитудного спектра сигнала.

% Файл - сценарий для построения графиков спектров

w_0 = pi/10; % основная частота

n1=1:1:15;    % положительные  номера гармоник

cof_pol=2*( ( (-1).^(n1+1) )+1 )./(pi.*n1*j);

n2=-15:1:-1;    % отрицательные номера

cof_otr=2*( ( (-1).^(n2+1) )+1 )./(pi.*n2*j);

Cn=[cof_otr 0 cof_pol];   %  коэффициенты Фурье для  n>0, n=0,n<0

n=-15:15;

subplot(1,2,1),stem(n*w_0,abs(Cn));

xlabel('Frequency,  rad/sec');

title('|Cn|');

subplot(1,2,2),stem(n*w_0,angle(Cn));

xlabel('Frequency,  rad/sec');

title('angle(Cn) in rad');

axis([-5,5,-1.75,1.75]);

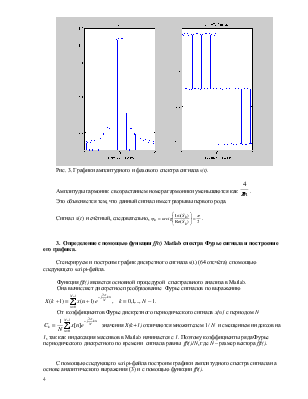
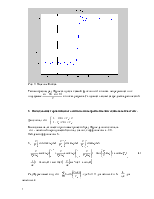
Полученный графики изображены на Рис.3.

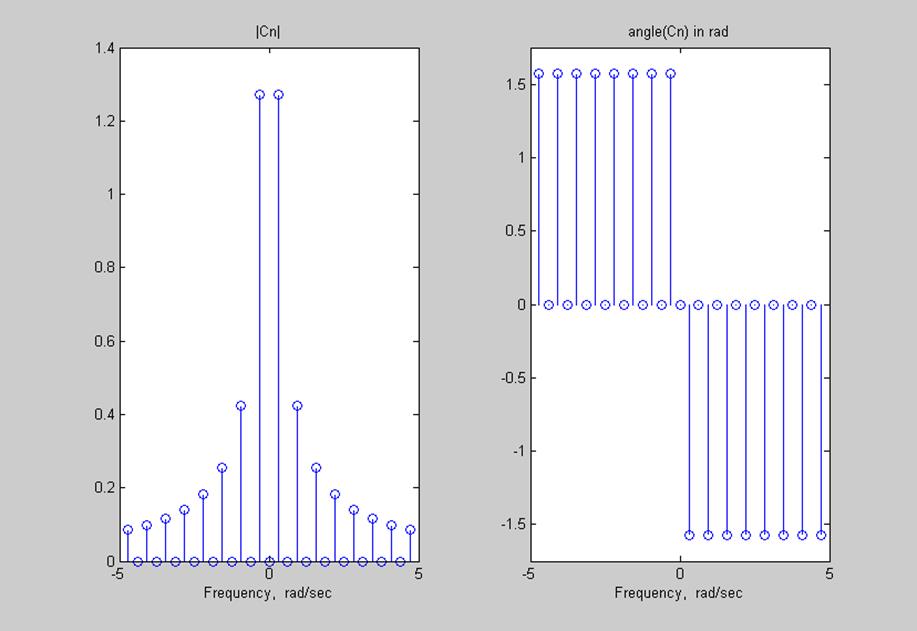
Рис. 3. Графики амплитудного и фазового спектра сигнала s(t).

Амплитуды гармоник с возрастанием номера гармоники уменьшаются как .

Это объясняется тем, что данный сигнал имеет разрывы первого рода.

Сигнал  нечётный, следовательно, .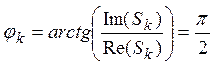

3.  Определение с помощью функции fft() Matlab спектра Фурье сигнала и построение его графика.

Сгенерируем и построим график дискретного сигнала s(t) (64 отсчёта) с помощью следующего script-файла.

Функция fft() является основной процедурой  спектрального анализа в Matlab.

Она вычисляет дискретное преобразование  Фурье сигналов по выражению  .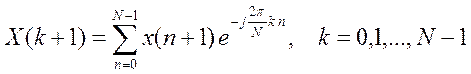 

От  коэффициентов Фурье дискретного периодического сигнала x[n] с периодом N 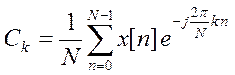     значения X(k+1) отличаются множителем  и смещением индексов на 1, так как индексация массивов в Matlab начинается с 1. Поэтому коэффициенты ряда Фурье периодического дискретного по времени  сигнала равны  fft()/N, где N – размер вектора fft().

С помощью следующего script-файла построим графики амплитудного спектра сигнала на основе аналитического выражения (3) и с помощью функции fft().

T=20;

t=-10:T/63:T;

x=(-1)*rectpuls(t+5,10)+1*rectpuls(t-5,10)+(-1)*rectpuls(t-15,10);

set(gca,'FontName','Arial Cyr', 'FontSize',10);

title(' График сигнала');

k=1:64;

C=2*( ( (-1).^(k+1) )+1 )./(pi*k);

subplot(3,1,2),stem(2*pi*k/T,abs(C));

set(gca,'FontName','Arial Cyr', 'FontSize',10);

title(' Амплитудный спектр сигнала');

axis([0,20.5,-0.01,1.5]);

y=fft(x,64);

subplot(3,1,3),stem(2*pi*k/T,abs(y)/64);

axis([0,20.5,-0.01,0.8]);

set(gca,'FontName','Arial Cyr', 'FontSize',10);

xlabel(' Угловая частота, рад/сек');

title(' Амплитудный спектр сигнала по процедуре fft');

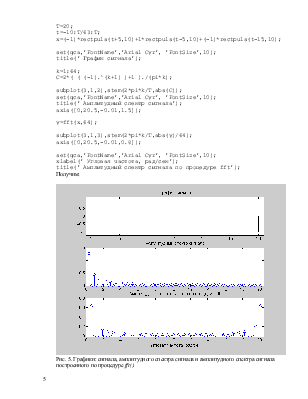
Получим:

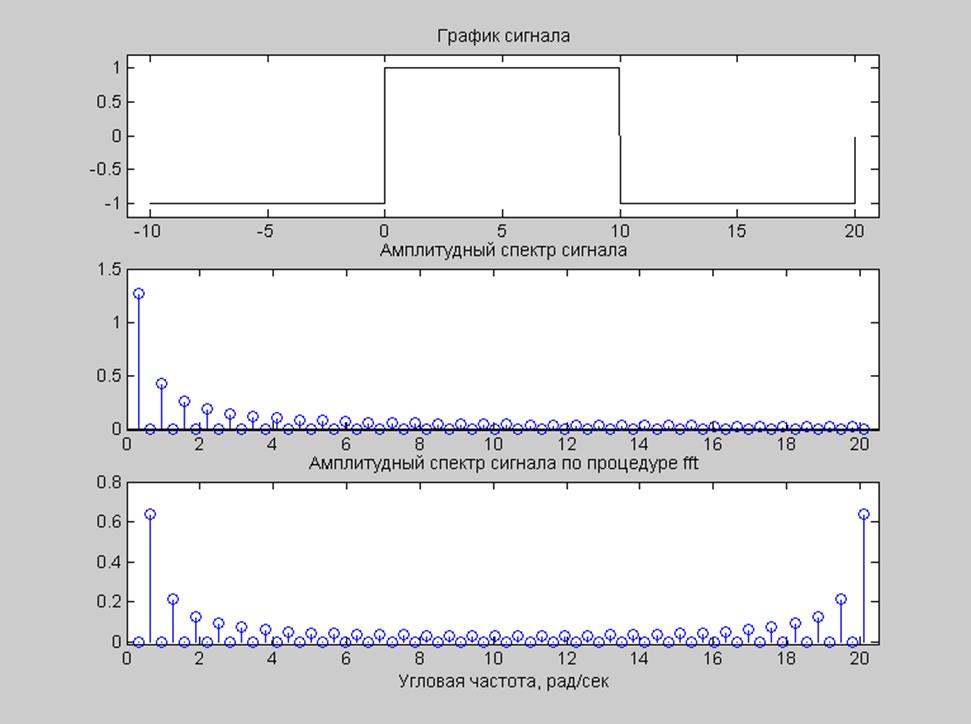
Рис. 5. Графики: сигнала, амплитудного спектра сигнала и амплитудного спектра сигнала построенного по процедуре fft():

Графики амплитудного спектра, вычисленного аналитически и с помощью функции fft(), совпадают до половины частотной шкалы, что объясняется периодичностью дискретного преобразования Фурье.

4.  Исследование сходимости ряда Фурье к исходному периодическому сигналу.

Исследуем сходимость ряда Фурье к исходному периодическому сигналу с помощью файл-сценария, приведённого ниже.

T=20;

w_0 = pi/10;

t = -10:T/1000:T; % интервал времени

% исходный сигнал

x1=(-1)*rectpuls(t+5,10)+1*rectpuls(t-5,10)+(-1)*rectpuls(t-15,10);

N = input('Number of harmonics = ');

c_0 = 0;

x = c_0*ones(1,length(t)); % постоянная   составляющая

for n=1:N,

% коэффициенты Фурье

cn = 2*( ( (-1).^(n+1) )+1 )./(pi.*n*j);

c_n = conj(cn);

% Приближение сигнала рядом Фурье

x = x + 0.5*cn*exp(j*n*w_0*t) + 0.5*c_n*exp(-j*n*w_0*t);

end

plot(t,x,t,x1,'--r'),grid;

axis([-9,21,-1.5,1.5]);

title(['N = ',num2str(N)]);

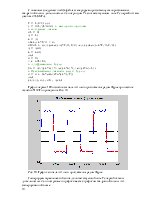
Запуская файл-сценарий с разными значениями числа членов ряда, пронаблюдаем его сходимость.

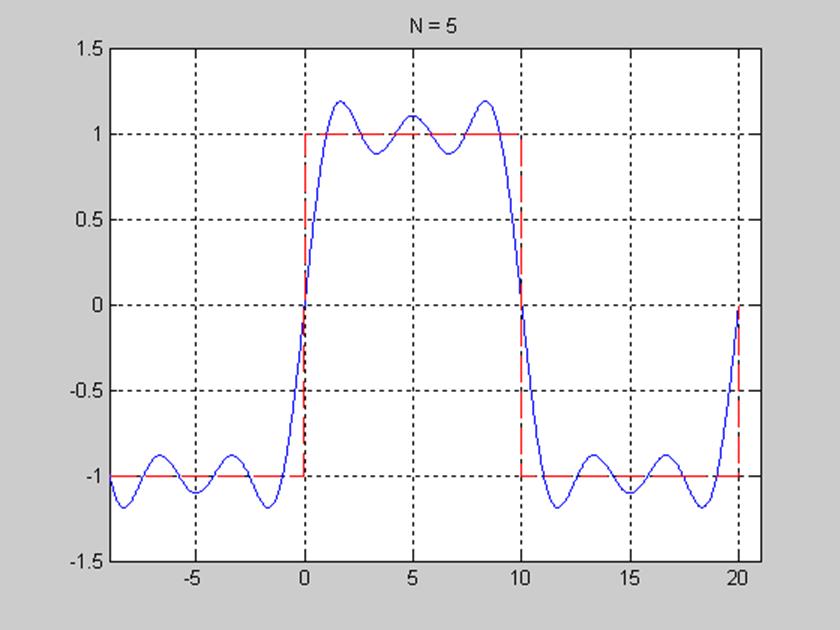
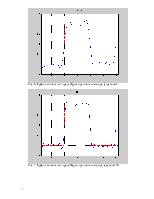
Рис. 6. График сигнала и его ряда Фурье при числе членов ряда, равном 5.

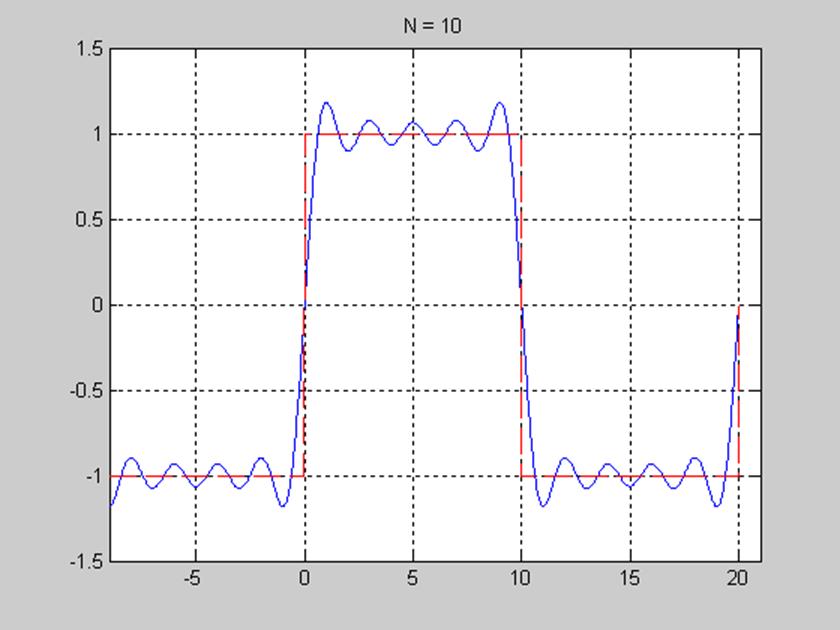
Рис. 7. График сигнала и его ряда Фурье при числе членов ряда равном 10.

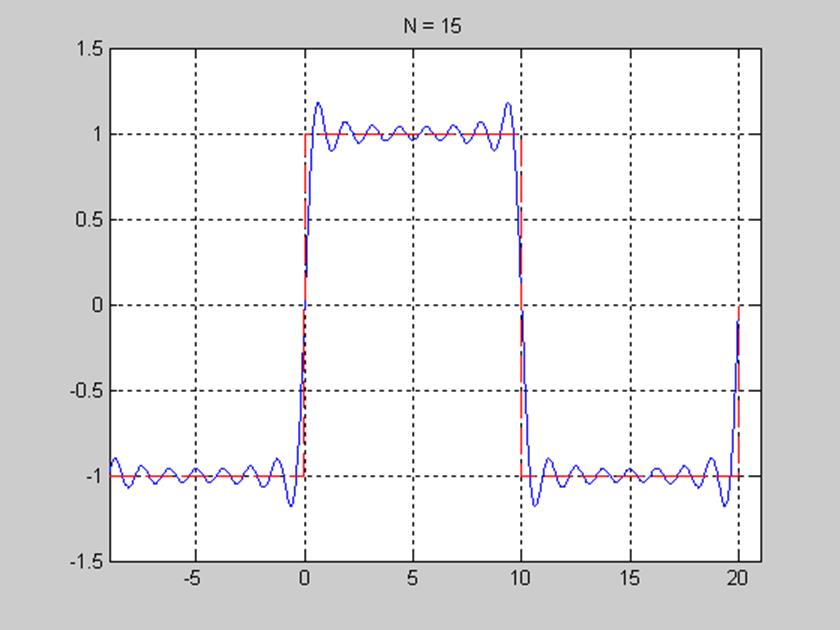
Рис. 8. График сигнала и его ряда Фурье при числе членов ряда равном 15.

Из  рис. 6-8 видим, что частичные суммы ряда Фурье сходятся к сигналу при числе гармоник N=5, N=10, N=15. C увеличением количества членов ряда N ряд Фурье ближе приближается к форме исходного сигнала. Особенностью сходимости  конечного ряда Фурье является её среднеквадратический характер, т.е. при увеличении  N  стремится к нулю квадрат разности между сигналом  x(t ) и его конечным рядом Фурье.

Увеличив фрагмент Рис.8, проиллюстрируем пульсации вблизи точек разрыва, которые объясняются явлением Гиббса, возникающим у сигналов с разрывами при усечении ряда Фурье конечным числом членов N.

При изменении количества членов ряда эффект Гиббса не исчезает. Не изменяется также относительная амплитуда пульсаций (по отношению к амплитуде прямоугольного импульса). Изменяется только частота пульсаций.

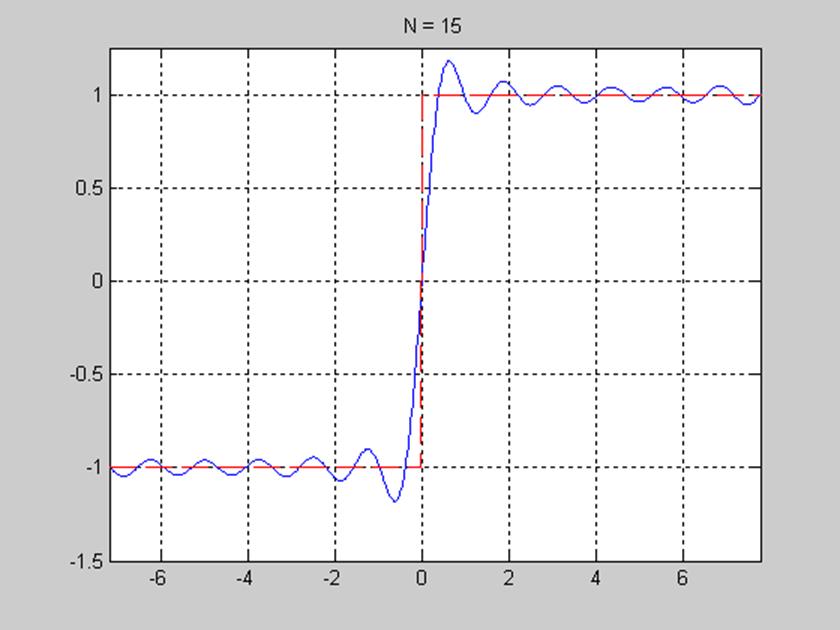
Рис. 9. Явление Гиббса.

Таким образом, ряд Фурье сходится к самой функции s(t) в точках непрерывности и к

полусумме 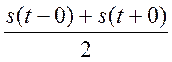 в точках разрыва. Сходимость является среднеквадратической.

5.  Исследование гармонического сигнала и квадратной волны одинаковой частоты.

Дан сигнал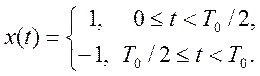

Вычислим аналитически тригонометрический ряд Фурье данного сигнала.

 - нечётный периодический сигнал, значит, коэффициенты a_k = 0.

Найдём коэффициенты b_k.

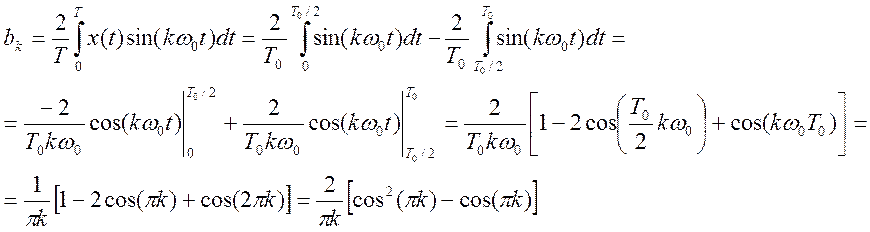         (4)                  

Ряд Фурье имеет вид 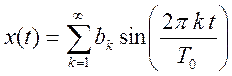, где  b_k = 0  для чётных k и 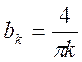 для нечетных k.

С помощью следующего script-файла сгенерируем приближенную аппроксимацию квадратной волны длительностью 2 с и периодом  T₀, соответствующим  ноте Ре  первой октавы (частота 293,66 Гц).

T = 1/293.66;

t = 0:1/8192:2; % интервал времени

% исходный сигнал

x1 = 0;

q = 1;

k = 3;

while k*T/4 < 2,

x1=x1 + rectpuls(t-q*T/4,T/2)-rectpuls(t-k*T/4,T/2);

q = q+4;

k = k+4;

end

x = 0;

for n=1:19,

% коэффициенты Фурье

bn = (2/(pi*n))*cos(pi*n)*(cos(pi*n)-1);

% Приближение сигнала рядом Фурье

x = x + bn*sin(2*n*pi*t/T);

end

plot(t,x,t,x1), grid

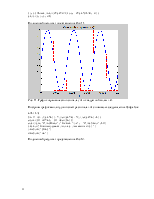
График первых 100 отсчётов сигнала x(t) и его приближения рядом Фурье при частоте отсчетов 8192 Гц приведён на Рис. 10.

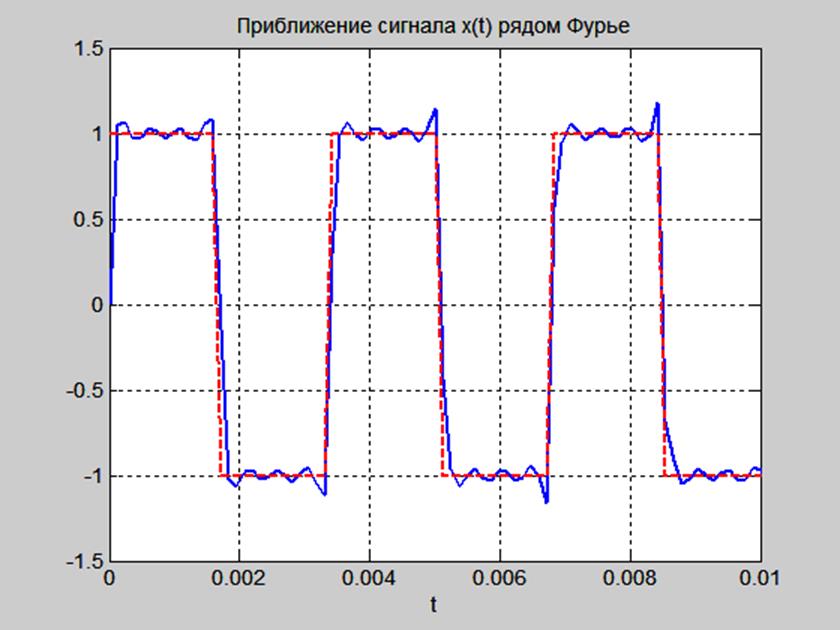
Рис. 10. График сигнала x(t) и его приближения рядом Фурье.

Сгенерируем гармонический сигнал, соответствующий ноте Ре первой октавы длительностью 2 с и построим его график вместе с графиком квадратной волны x(t), сгенерированной выше.

[y,t]=harmonic(2*pi*293.66, 2*pi*8192, 2);

plot(t,y,t,x1)

Полученный результат представлен на Рис. 11.

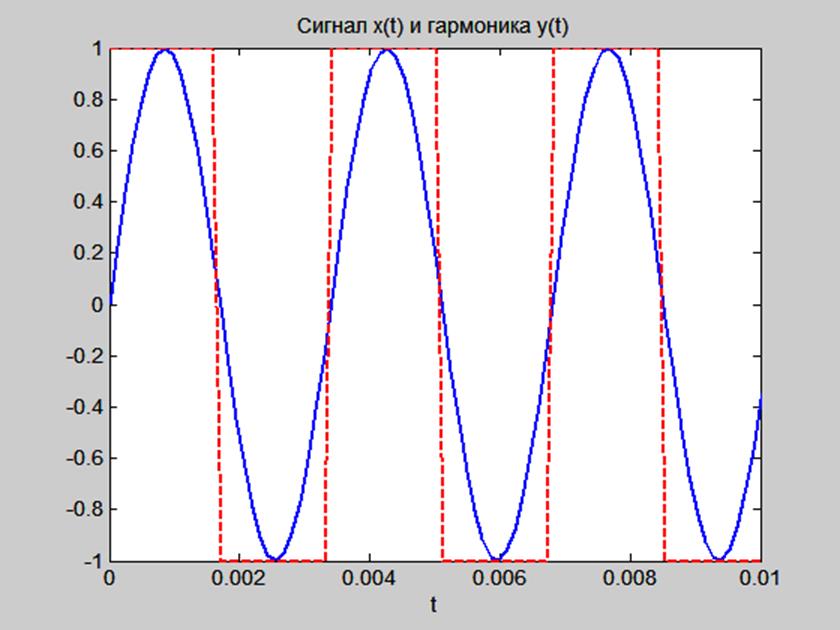
Рис. 11. График гармонического сигнала y(t) и квадратной волны x(t).

Построим график амплитудного спектра сигнала x(t) с помощью следующего script-файла:

k=1:19;

bn = (2./(pi*k)).*cos(pi*k).*(cos(pi*k)-1);

stem([0 w0*k], [0 abs(bn)])

set(gca,'FontName','Arial Cyr', 'FontSize',10)

title('Амплитудный спектр сигнала x(t)')

ylabel('|Ak|')

xlabel('wk')

Полученный результат представлен на Рис.12.

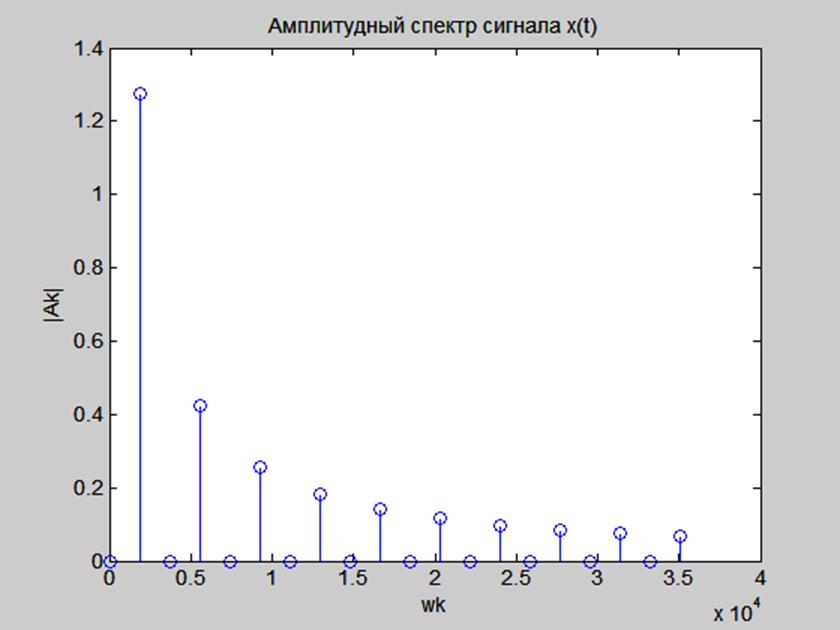
         Рис.12.   График амплитудного спектра сигнала x(t).

Сигнал y(t) представляет собой одну гармонику с частотой 293,66 Гц и амплитудой А = 1.

Поэтому его амплитудный спектр имеет вид, представленный на Рис. 13.

Рис. 13. Амплитудный спектр гармоники y(t).

Сигналы x(t) и y(t) сходны по звучанию. Звучание ряда Фурье сигнала x(t) (рис. ) ближе к звучанию гармоники y(t), чем сам сигнал x(t).

Вывод:

1.                     Любой конечный периодический сигнал x(t), определенный для всех действительных t или на конечном интервале времени ,  можно представить  рядом Фурье (суммой гармоник или комплексных экспонент).

2.                     Амплитудный и фазовый спектры сигнала представляют зависимость значения амплитуды и начальной фазы от частоты гармоники и дают полное описание гармоник, входящих в ряд Фурье сигнала.

3.         Основной процедурой  спектрального анализа в Matlab является функция fft(). Коэффициенты ряда Фурье периодического дискретного по времени сигнала с помощью функции fft() можно найти как  fft()/N, где N – размер вектора fft().

4.         Спектры сигнала, получаемые с помощью функции fft() имеют периодический характер, что объясняется периодичностью дискретного преобразования Фурье.

5.         Ряд Фурье сигнала сходится к самому сигналу в точках непрерывности и к полусумм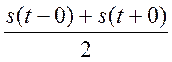е  в точках разрыва. Сходимость является среднеквадратической, т.е. 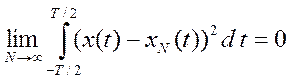, где x(t) – сигнал, x_N(t) – приближение сигнала x(t) рядом Фурье.

6.         Вблизи точек разрыва сигнала  наблюдаются пульсации, которые объясняются явлением Гиббса, возникающим у сигналов с разрывами при усечении ряда Фурье конечным числом членов k.