Решение обыкновенных линейных разностных уравнений с постоянными коэффициентами

Решение обыкновенных линейных разностных уравнений

с постоянными коэффициентами

Связь выхода и входа линейной дискретной системы может быть описана обыкновенным линейным разностным уравнением с постоянными коэффициентами

,

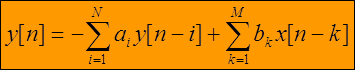где  y[n]- выходной сигнал в момент n,

        x[n] - входной сигнал в момент n,

        a_i,  b_k – постоянные коэффициенты.

Для решения таких уравнений могут использоваться два метода

• Прямой метод,
• Метод Z – преобразования.

Вначале рассмотрим  решение линейного разностного уравнения с помощью прямого метода.

Общее решение неоднородного (с отличной от нуля правой частью) линейного разностного уравнения равно сумме общего решения линейного однородного разностного уравнения и частного решения неоднородного уравнения

  

Общее решение однородного разностного уравнения (zero-input response) y_h[n]

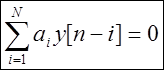
 определяется в виде

.

Подставляя это решение в однородное уравнение, получаем

или                                .

            Такой полином называют характеристическим полиномом системы. Он имеет N корней   . Корни могут быть действительными или комплексными и некоторые корни -  совпадающими (кратными).

Если корни  являются действительными и разными, то решение однородного уравнения имеет вид

    ,

где коэффициенты    определяются по начальным условиям.

Если некоторый корень, например,  λ₁ имеет кратность m, то соответствующий ему член решения  приобретает форму 

    .

Если  все коэффициенты однородного уравнения и соответственно характеристического многочлена действительны, то два члена решения, соответствующие простым комплексно сопряженным корням    можно представить (записать) в  виде   , при этом коэффициенты  A, B определяются по начальным условиям.

Вид частного решения y_p[n] уравнения  зависит от правой части (входного сигнала) и определяется согласно нижеприведенной таблице

Таблица 1.   Вид частного решения для различного характера  правой части

Входной сигнал x[n]	Частное решение  yp[n]
A  (константа) AMn AnM	K KMn

  Решение линейного разностного уравнения методом Z – преобразования заключается в применении Z – преобразования к уравнению с использованием свойств линейности  и временного сдвига. В результате получается  линейное алгебраическое уравнение относительно Z - изображения искомой функции. Обратное Z – преобразование дает искомое решение во временной области. Для получения обратного Z – преобразования чаще всего используется разложение рационального выражения на простые (элементарные) дроби, так как обратное преобразование от отдельной элементарной дроби имеет простой вид.

Заметим, что для перехода во временную область могут использоваться и другие методы вычисления обратного Z – преобразования.

 Пример.  Определим отклик (выходной сигнал)  системы, описываемой линейным разностным уравнением     , на входной сигнал 

Решение. 

1.  Прямой метод решения уравнения.

Однородное уравнение   .  Его характеристический полином    .

Корни полинома   .

Решение однородного уравнения    .

Поскольку  ,то  частное решение определяем в виде   .

Подставляем его в уравнение

.

Для нахождения константы К  примем   n = 2.   Тогда

,  или  ,   К=2,33

Отсюда  частное решение  и   общее решение разностного уравнения                                                                                      (1)

Найдем константы С₁ и С₂.  Для этого положим  n = 0, тогда из исходного разностного уравнения получаем  . Для данного уравнения 

, поэтому  .  Из выражения (1)

, следовательно, 

 .

Далее положим n = 1, при этом из уравнения следует  . Поскольку , то

.   Из выражения (1) для n = 1 имеем .
 Получаем  следующие два уравнения для С₁ и С₂

.

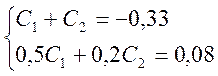Решение этой системы дает следующие значения:   С₁ =0,486  и  С₂ = -0,816.

Следовательно,   общее решение данного уравнения 

2.  Решение методом  Z – преобразования.

Возьмем  Z – преобразование от исходного разностного уравнения ,  учитывая свойство (теорему) временного сдвига 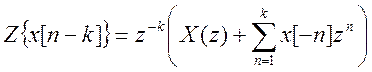 .  Получаем 

Для данного уравнения ,  в связи с этим

. Разрешая это уравнение относительно  Y(z), имеем

. 
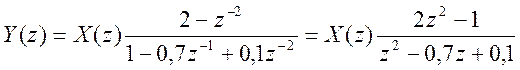Для данного случая   его Z - преобразование  .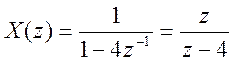

Подставляя его в предыдущее выражение, получаем  решение уравнения в Z – области

.

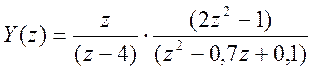Найдем корни  полинома 

.

Для получения решения уравнения во временной области  представим Y(z) в виде суммы элементарных дробей

.

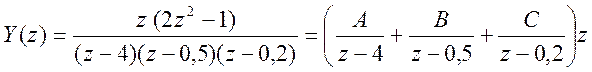Определим коэффициенты  A, B, C 

,     ,

.

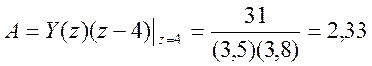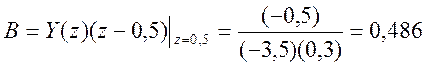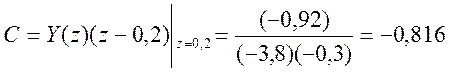Поэтому представление Y(z) как суммы элементарных дробей имеет вид

.

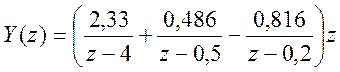Обратное Z – преобразование от 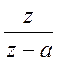  равно 

Следовательно, решение уравнения во временной области имеет вид

Составил:      доц.  Щетинин Ю.И.