Разработка цифрового БИХ-ФВЧ Баттерворта, страница 3

Получим АЧХ каскадной формы с округлением:

[z,p,k]=tf2zp(numd, dend)

sos=zp2sos(z,p,k)

[z, p, k]=sos2zp(sos)

[b_q, a_q]=zp2tf(z, p, k);

[H_q, f1]=freqz(b_q, a_q, 256, Ft);

figure(3)

hold on

plot(f, abs(H),'g','LineWidth',2),

plot( f1,abs(H_q), 'b'),

set(gca,'FontName','Times New Roman Cyr','FontSize',10)

grid on

legend('АЧХ спроектированного фильтра', 'АЧХ каскадного фильтра')

xlabel('Частота, Гц')

sos =

  0.00175225785417     -0.00135965324556      0

  1.00000000000000     -0.24379838906509     0

  1.00000000000000     -2.53952222895923      1.61558182696610

  1.00000000000000     -0.49153269144504      0.06798950631853

  1.00000000000000     -2.43847917577143                  1.51103832193082  

  1.00000000000000     -0.50358928380089      0.09418575446632

  1.00000000000000     -2.27586838906861      1.34356001048993

  1.00000000000000     -0.52454581599867      0.13971957046668

  1.00000000000000     -2.09080630925029      1.15404066484925

  1.00000000000000     -0.55581735189653     0.20766554887937

  1.00000000000000     -1.90949144504352      0.96878603922254

  1.00000000000000     -0.59965669193688      0.30291853508911

  1.00000000000000     -1.57395946203672      0.62483383844160

  1.00000000000000     -0.65950171414082      0.43294824845380

  1.00000000000000     -1.64125672697907      0.69405783956813

  1.00000000000000     -0.74055879058406      0.60906696574850

  1.00000000000000     -1.75467267541226      0.81039948287221 

  1.00000000000000     -0.85078957390062      0.84857355764226

Так как спроектированный фильтр имеет 17-й порядок, то можно его представить как каскадное соединение восьми фильтров 2-ого порядка и одного фильтра 1-ого порядка.

Каскадная форма представления передаточной функции данного фильтра будет иметь вид:

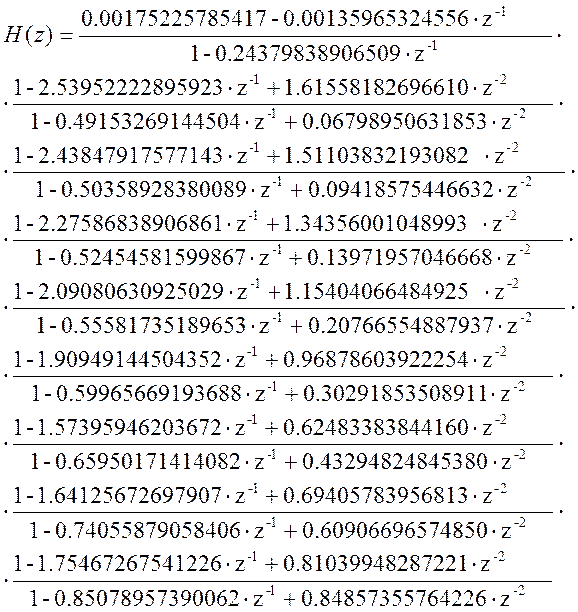
Структурная схема последовательной формы:

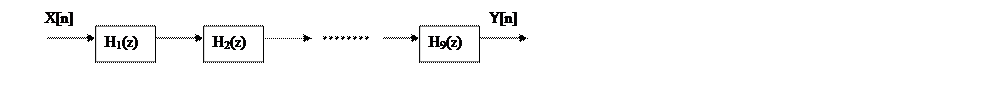
где       

             

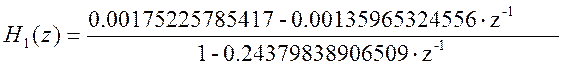
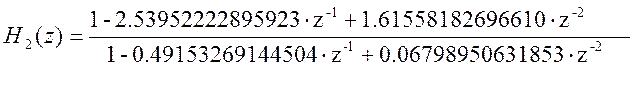
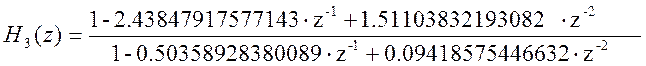
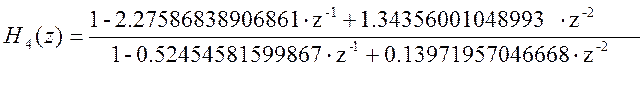
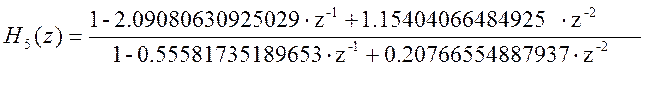
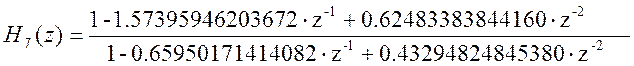
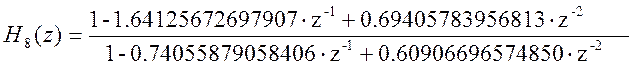
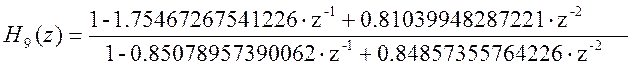
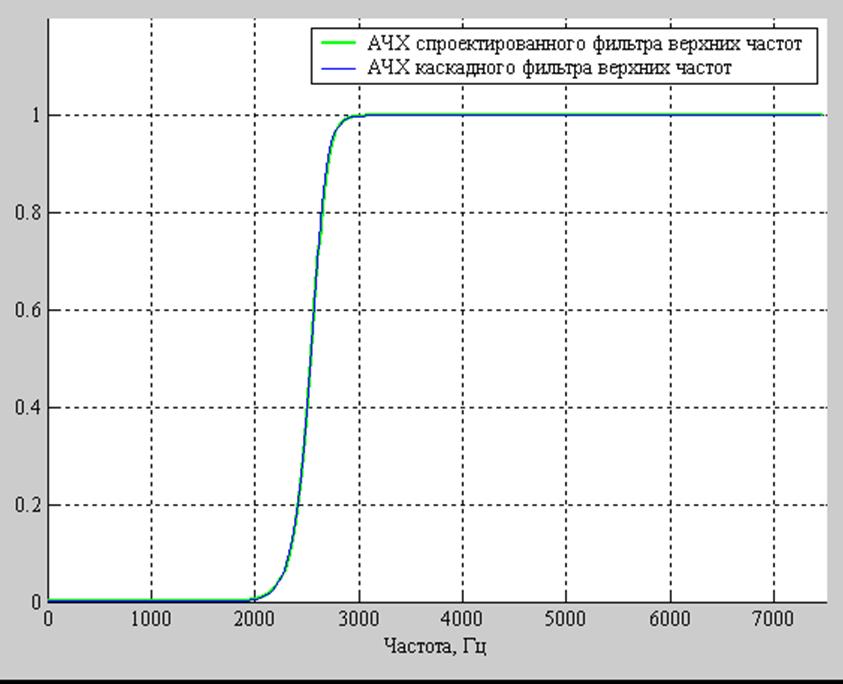
Рис. 6  АЧХ исходного и каскадного фильтров.

Видно, что АЧХ каскадной формы с округлением не отличается от АЧХ исходной, то есть такая реализация вполне подходит для данного фильтра.

Тестирование фильтра

Пусть входной сигнал представляет собой сумму дискретных гармоник с частотами 1000 Гц (шум) и 5000 Гц (полезный сигнал). Первая гармоника входит в полосу задерживания фильтра, вторая - в полосу пропускания:

N=500; Tt=1/Ft; i=0:1:N-1;

s=2*sin(2*pi*1000*Tt*i);

s1=sin(2*pi*5000*Tt*i);

x=s+s1;

subplot(411)

plot(i, s),   set(gca,'FontName','Times New Roman Cyr','FontSize',10)

title('Сигнал с частотой 1000 Гц' )

subplot(412)

plot(i, s1),set(gca,'FontName','Times New Roman Cyr','FontSize',10)

title('Сигнал с частотой 5000 Гц')

subplot(413)

plot(i, x),set(gca,'FontName','Times New Roman Cyr','FontSize',10)

title('Сигнал, содержащий низкочастотые шумы')

subplot(414)

F=filter(numd, dend, x)

plot(i, F),set(gca,'FontName','Times New Roman Cyr','FontSize',10)

title('Сигнал после фильтрации')

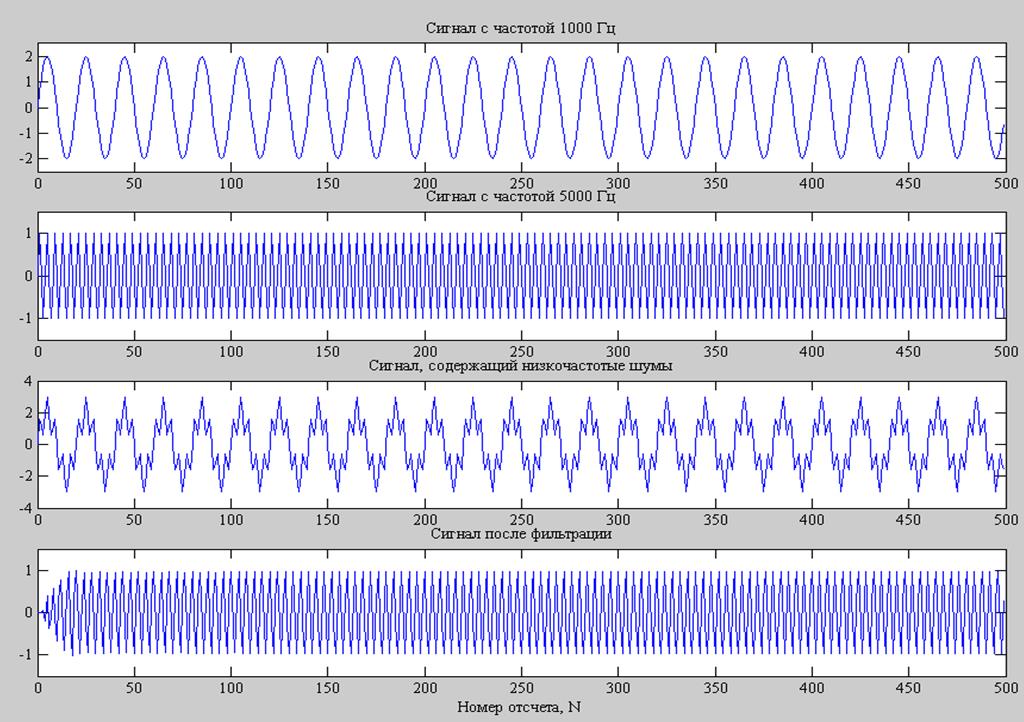
Рис. 7.   Сигналы с частотами 1000 и 5000 Гц, суммарный сигнал и сигнал на выходе фильтра.

Пронаблюдаем, каким будет сигнал после фильтрации при подаче сигналов с частотами 2350 Гц и 3000 Гц, которые являются граничными частотами задерживания  и пропускания проектируемого фильтра соответственно:

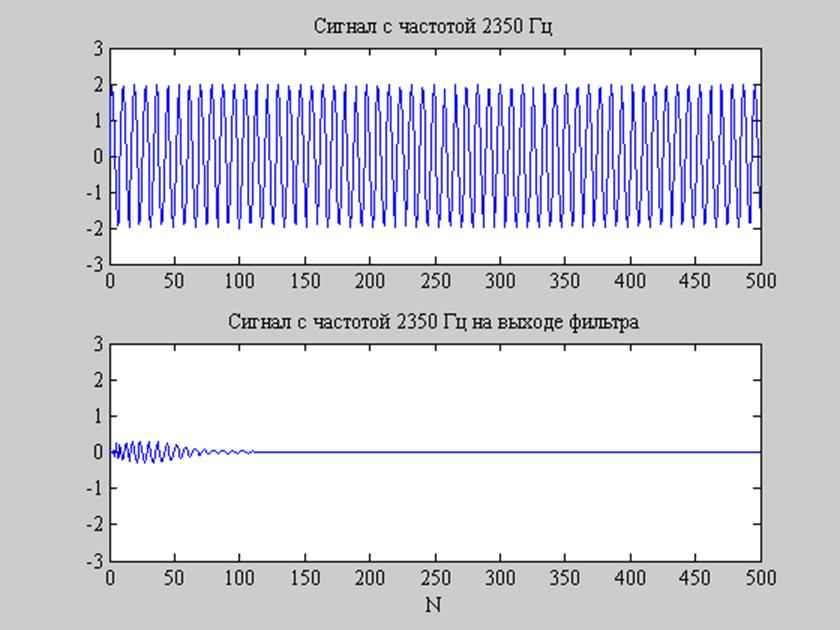
Рис. 8. Сигнал с частотой 2350 Гц на входе фильтра (верхний график) и на выходе (нижний график).

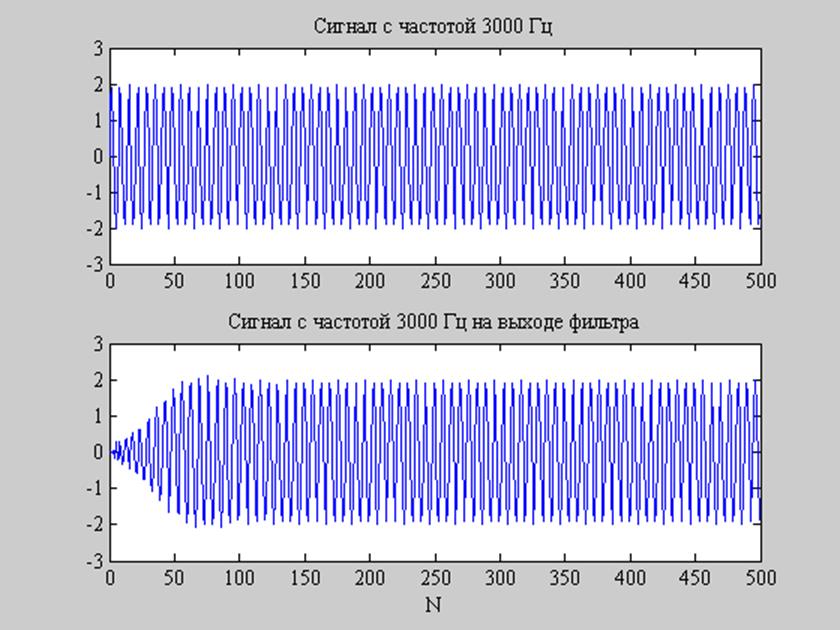
Рис. 9. Сигнал с частотой 3000 Гц на входе фильтра (верхний график) и на выходе (нижний график).

Как видно из представленных графиков, фильтр пропускает сигнал с частотой 3000 Гц, представляющую в спроектированном фильтре частоту среза и подавляет сигнал с частотой 2350 Гц – граничной частотой задерживания фильтра.

Далее, необходимо рассмотреть, как фильтр будет реагировать на сигнал с частотой 7000 Гц.  На рис. 10 приведены графики на входе и выходе фильтра. И судя по ним, можно сказать, что фильтр пропускает сигнал практически без подавления.

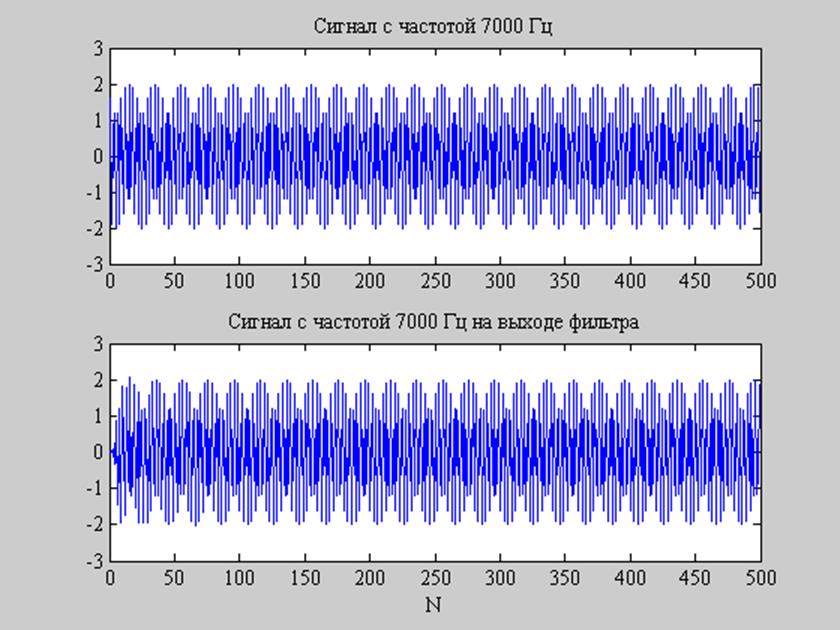
Рис. 10. Сигнал с частотой 7000 Гц на входе фильтра (верхний график) и на выходе (нижний график).

В итоге, по представленным графикам можно сделать вывод о том, что спроектированный фильтр полностью соответствует заданной спецификации: подавляет сигналы, имеющие частоту менее либо равную 2350 Гц, и пропускает сигналы с частотами 3000 Гц и выше.

Программирование фильтра и оценка его быстродействия

          Для оценки быстродействия полученного фильтра была разработана программа на языке C++, в качестве компилятора использовался Microsoft Visual C++ 6.0.

В написанной программе расчет входного сигнала производится в главной функции программы, а выходного сигнала - в отдельном потоке, где для его вы­числения организован цикл. Для анализа быстродействия вычисления выходного сигнала была использована функция API GetTickCount(), которая возвращает количество миллисекунд, прошедших с начала ра­боты. Перед циклом вычисления выходного сигнала переменной n присваива­ется значение GetTickCount(), а по завершению цикла еще раз вызывается функция GetTickCount() и по разности между ее значением и значением переменной n определя­ется время вычисления цикла. Данный метод дает приблизительную оценку времени вы­числения цикла, более того эта оценка зависит от конфигурации и свободных системных ресурсов компьютера, на котором запускается программа. При запуске программы на компьютере с процессором Intel Pentium4 (512k L2) 2,4 GHz для N=10000, где N - количество отчетов, он  выполнялся порядка t=32 мс, значит время обработки одного отсчета (Т) в режиме реального времени будет равно: Т = время  обработки всех отсчетов(t)/количество отсчетов = t/N=3,2 мкс. Можно менять число отсчетов N, например:

N	t	T
10000	32мс	3,2мкс
20000	156мс	7,8мкс
50000	718мс	14,36мкс
100000	1503мс	15,03мкс

Листингпрограммы:

#include <iostream>

#include <math.h>

#include <stdio.h>

#include <windows.h>

#include <conio.h>

#define N 10000                            // количество отчетов

double pi = 3.141592623582;

double fd = 15000;                             // частота дискретизации

double Td = 1/fd;                                // период дискретизации 

double x1[3]={  0.00175225785417 ,       -0.00135965324556,          0 };