Информатика и выч. техника \ Теория и обработка сигналов

Разработка цифрового БИХ-ФВЧ Баттерворта, страница 2

         В данной работе я буду применять именно метод, основанный на использовании аналогового прототипа, а переход к цифровому фильтру будет осуществлен на основе метода билинейного преобразования. Этот метод преобразования аналогового фильтра в цифровой применяется наиболее часто ввиду его простоты и качеств результирующих характеристик фильтров. 

Метод билинейного преобразования:

        С помощью этого метода передаточная функция W(p) «р-плоскости» преобразуется в передаточную функцию W(z) «z-плоскости» цифрового БИХ-фильтра с помощью функции:

                                                                

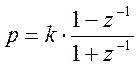
где k–положительная константа.

Ось частот Ω в аналоговом случае преобразуется в единичную окружность так, что

                                                       

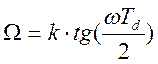
и поэтому частота среза Ωс АЧХ аналогового фильтра будет соответствовать частоте среза  АЧХ цифрового фильтра.

          Устойчивость полученного таким образом цифрового фильтра гарантируется, если исходный аналоговый фильтр был устойчив и область устойчивости в одной комплексной плоскости путем преобразования отображается в область устойчивости в другой комплексной плоскости. Достоинством метода билинейного преобразования является то, что передаточная функция цифрового фильтра определяется с помощью простых формул из передаточной функции аналогового фильтра, для которых существуют подробные таблицы и справочники. Также метод билинейного преобразования по сравнению с другими методами преобразования аналоговых фильтров в цифровые (инвариантности импульсной характеристики и согласованного z-преобразования) обеспечивает построение  такого БИХ-фильтра, выходной, сигнал которого приближенно совпадает с выходным сигналом аналогового фильтра-прототипа при произвольных одинаковых входных сигналах. Метод билинейного преобразования имеет и свои недостатки, наиболее значимым из которых является несоответствие импульсной и фазовой характеристик аналогового и цифрового фильтра.

Проектирование фильтра

Спецификация:

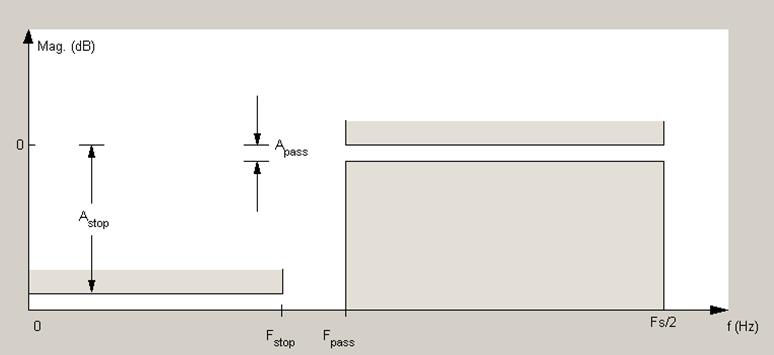
Рис. 1. График спецификации фильтра.

Частота среза        Fpass = 3 кГц;

Граничная частота полосы задерживания      Fstop=2,35 кГц;

Минимальное ослабление в полосе задерживания      Astop=Rs=40 дБ;

Максимальное ослабление в полосе пропускания       Apass=Rp=2 дБ;

Частота дискретизации      Ft=15 кГц;

1. Определение нормированных частот:

wstop=2*pi*Fstop/Ft

wpass=2*pi*Fpass/Ft

wstop =  

0.9844

wpass =

1.2566

2. Определение граничных частот аналогового фильтра:

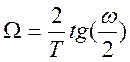
Wstop=2*Ft*tan(wstop/2)

Wpass=2*Ft*tan(wpass/2)

Wstop =

 1.6086e+004

Wpass =

 2.1796e+004

3. Проектирование нормированного фильтра нижних частот:

Граничная частота полосы задерживания:

Omega_s= Wpass/Wstop

Omega_s = 1.3550

Параметры НФНЧ:

, , Amin=Rs=40 дБ, Amax=Rp=2 дБ.

Определим порядок НФНЧ:

[N,Wn]=buttord(1,Omega_s, 2, 40, 's')

N =

            17

Wn =

1.0335

Передаточная функция НФНЧ может быть определена как:

>> [num,den]=butter(N,Wn,'s');

4.  Преобразование НФНЧ в фильтр высоких частот:

 Переход от НФНЧ к ФВЧ осуществляется на основе замены в передаточной функции вида: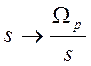                                                                   

[BV,AV]=lp2hp(num,den,2*pi*Fpass);

5. Преобразование аналогового прототипа в соответствующий цифровой фильтр:

 [numd,dend]=bilinear(BV,AV,Ft)

numd =

0.00175225785417                          -0.02978838352096              0.23830706816770

-1.19153534083841             4.17037369293415              -10.84297160162812

21.68594320325509           -34.07791074797070             42.59738843496155

-42.59738843495988         34.07791074796673           -21.68594320325092

10.84297160162517            -4.17037369293266               1.19153534083788

-0.23830706816757            0.02978838352095            -0.00175225785417

dend =

1.00000000000000          -5.16979030276860              14.46367040922036

-27.50767940615411           39.12579733432760           -43.60532242547756

39.11471706798366            -28.66802737958898              17.30075253380677

-8.61396569325646           3.52785935242574            -1.17875648613440

0.31671790038853             -0.06687410000679           0.01069902300251

-0.00122045679537            0.00008852050000         -0.00000307040745

6. Построим диаграмму нулей и полюсов, чтобы убедиться в том, что система устойчива:

zplane(numd,dend)

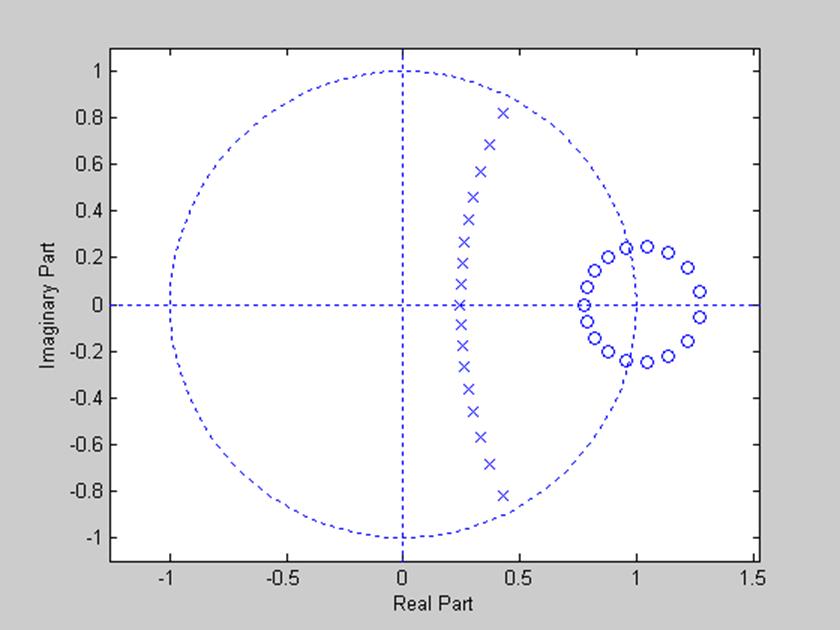
Рис. 2.   Диаграмма нулей и полюсов.

Из полученной диаграммы видно, что все полюса лежат внутри единичной окружности, и нет полюсов на окружности, значит, полученная система устойчива.

7. Построим график АЧХ цифрового ФВЧ Баттерворта:

[H,f]=freqz(numd,dend,500,Ft);

 subplot(2,1,1)

 plot(f,abs(H)),

 set(gca,'FontName','Times New Roman Cyr','FontSize',10)

 title('АЧХ полосового цифрового фильтра')

 xlabel('Частота, Гц ')

 grid on

 subplot(2,1,2)

 plot(f,20*log10(abs(H))),

 set(gca,'FontName','Times New Roman Cyr','FontSize',10)

 title('ЛАЧХ полосового цифрового фильтра')

 xlabel('Частота, Гц '),

 grid on

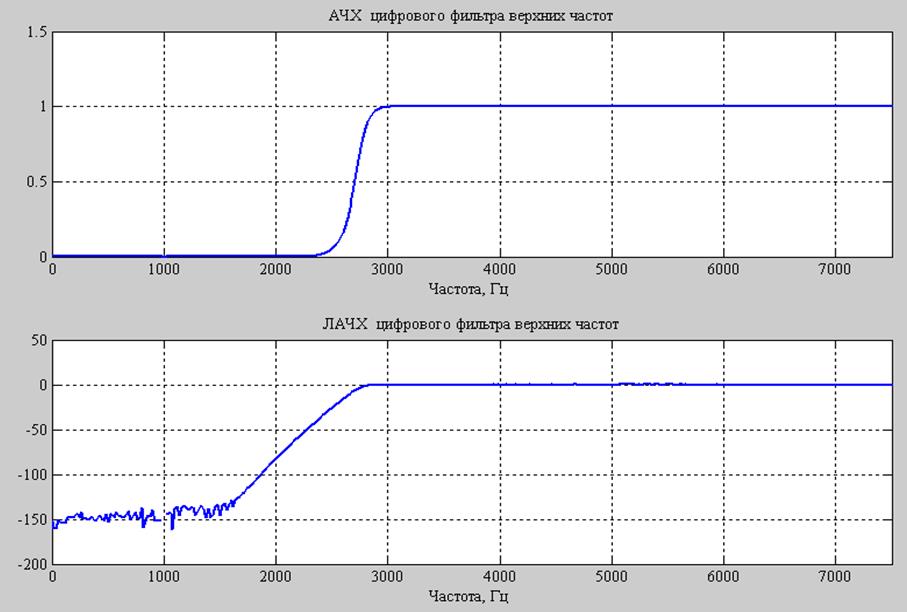
Рис. 3.     АЧХ и ЛАЧХ полученного фильтра.

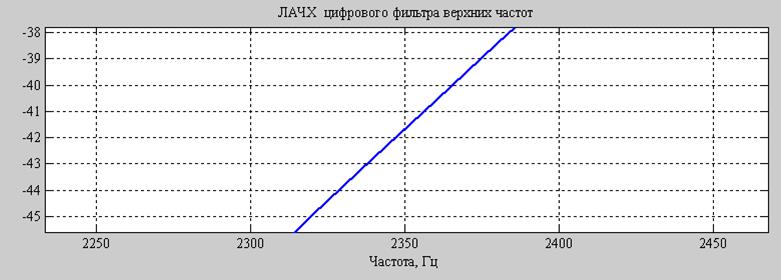
Рис.4.     ЛАЧХ  полученного фильтра,  область F=2,35 кГц (увеличено).

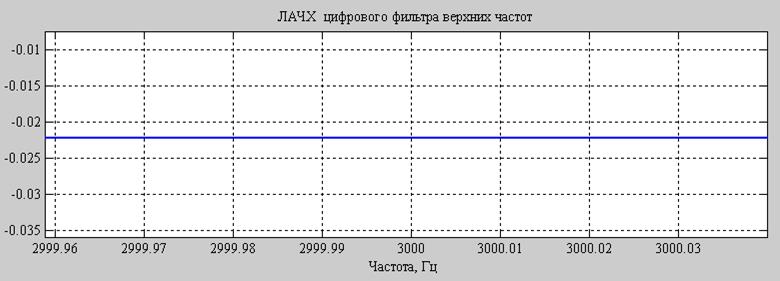
Рис.5.     ЛАЧХ  полученного фильтра,  область F=3 кГц (увеличено).

По графику АЧХ видно, что он полностью соответствует требуемым граничным частотам: Fpass=3000 Гц, Fstop=2350 Гц.

В результате проектирования был получен фильтр, полностью соответствующий заданным спецификациям.

Реализация фильтра

           Аппаратная реализация цифровых фильтров основана на использовании той или иной формы разностного уравнения или передаточной функции. Существуют так называемые прямые формы реализации БИХ – фильтров. Среди них выделяют Прямую форму 1: для нее характерно избыточное по сравнению с другими формами количество элементов и ярко выраженная чувствительность характеристик фильтра к погрешностям коэффициентов. Также существует Прямая форма 2: по сравнению с формой 1 в ней используется меньшее количество элементов суммирования и задержки. Еще можно выделить параллельную и последовательную формы построения ЦФ.

           В этой работе используется последовательная форма реализации цифрового фильтра, так как она менее чувствительна к погрешностям квантования, возникающим при округлении коэффициентов, например, по сравнению с прямыми формами.

Скачать файл