Преобразование функции f(x)= exp(-(x+1)/x) численными методами, страница 2

Промежуточные точки:

Величина остатков dy удовлетворяет условию dy=0.00002<e , значит полином третьей степени достаточно точно аппроксимирует заданную функцию f(x).

Квадратичные отклонения для m=0,1,2,3.

Сформируем матрицу остатков

3.2 Метод наименьших квадратов с использованием ортогональных многочленов Чебышева

Отрезок: a=1 , b=5 Шаг: h=0.5

Число узлов интерполирования: n=9

Начальная степень полинома: m=1

Cтепень полинома: m=2

Cтепень полинома: m=3

Cтепень полинома: m=4

Cтепень полинома: m=5

Cтепень полинома: m=6

Рис.1 График приближенной функции, полученной при помощи МНК с

использованием ортогональных многочленов Чебышева

Рис.2 Исходный график функции

Значения, полученные при аппроксимации полиномами различных степеней (1, 2, 3, 4, 5, 6) заданной функции, и отклонения от точных значений.

3.3 Метод интерполирования с применением сплайн-функций

Интерполировать функцию (x)= exp(-(x+1)/x) с применением сплайн-функций заданную на отрезке [1;5].

Разобьем числовую ось x на интервалы. Пусть известны значения функции f(x) на границах интервалах. Функцию f(x) можно аппроксимировать на каждом интервале кубическим многочленом:

S_i=a_i(x-x_i)³+b_i(x-x_i)²+c_i(x-x_i)+d_i

Значения коэффициентов многочлена должны удовлетворять четырем условиям:

1) В каждой нижней границе интервала сплайн проходит через опорную точку.

2) В каждой верхней границе интервала сплайн проходит через опорную точку.

3) Для каждой нижней граничной точки интервала сплайн имеет одинаковую крутизну в обоих граничащих интервалах.

4) Для каждой верхней граничной точки интервала сплайн имеет одинаковую крутизну в обоих граничащих интервалах.

Для решения системы уравнений относительно коэффициентов сплайнов необходимо добавить следующие граничные условия:

A: Через обе граничные точки кривая должна проходить с нулевой кривизной, превращаясь в прямую.

Б: Крутизна любого интерполирующего сплайна в обеих граничных точках фиксирована.

Исходя из данных условий, можно составить систему уравнений, и, решив ее, получить значения коэффициентов a,b,c,d каждого сплайна. Эту задачу решает следующая функция:

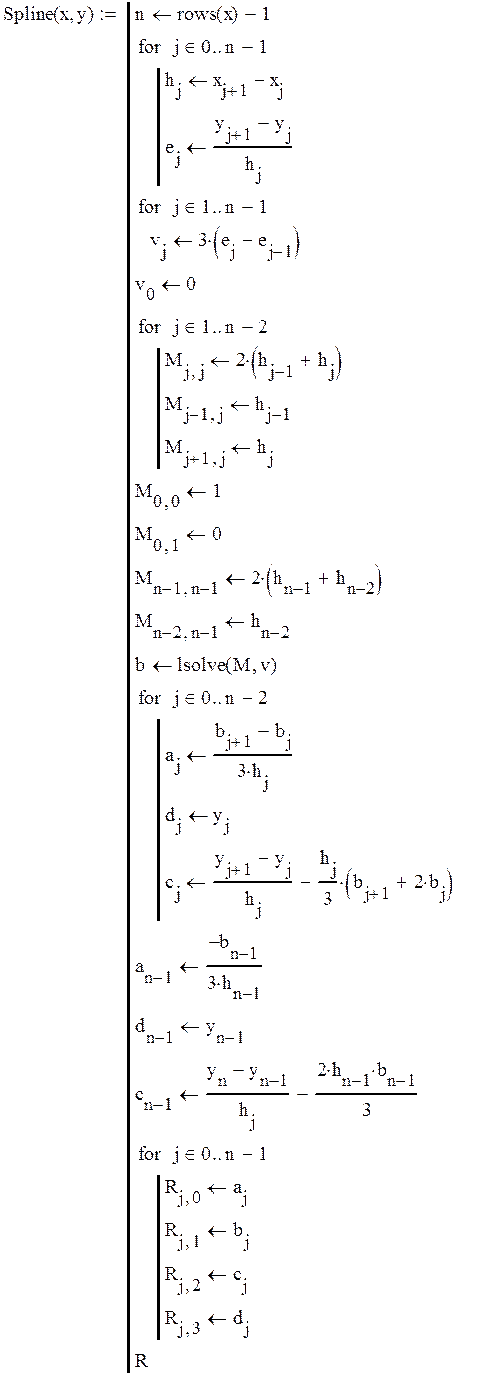
Функция, вычисляющая значение аппроксимирующей функции по найденным с помощью функции Spline(x,y) коэффициентам

Выбор опорных точек и значение функций в них

Эталонным результатом в задаче интерполирования является график заданной функции. Поэтому для оценки аппроксимирующей функции, полученной, как совокупности кубических полиномов построим ее на одном графике с эталоном (рис.3)

Рис.3 Результат интерполирования функции кубическими сплайнами

На рис.3 видно, что эталонный и аппроксимирующий графики совпадаю на всей области. Можно сделать вывод, что разбиение данного интервала на 8 частей дает хорошую аппроксимацию.

3.4 Метод интерполирования тригонометрическими многочленами