Кодирование исходного сигнала различными методами

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ  АВТОМАТИКИ  И  ВЫЧИСЛИТЕЛЬНОЙ   ТЕХНИКИ

Дисциплина  «Информационные сети»

ЛАБОРАТОРНАЯ  РАБОТА  № 1

Группа: АИ-52

Студент: Повещенко А.                         

Кильмухаметов Р. А.

Преподаватель: Моторин С. В.

Новосибирск, 2008

1. Кодирование исходного сигнала различными методами.

Функция позволяющая реализовать метод кодирования AMI.

function x = AmiCod(v)

len = length(v);

x = zeros(1, len);

odd = 0;

for i = 1:len

    if (v(i) == 1)

        if (odd == 0)

            x(i) = 1;

            odd = 1;

        else

            x(i) = -1;

            odd = 0;

        end

    else

        x(i) = 0;

    end

end

Манчестерскийкод.

function x = ManchesterCod(v)

len = length(v);

x = zeros(1, 2*len+2);

k = 3;

if (v(1) == 0)

    x(1) = 0;

    x(2) = 1;

else

    x(1) = 0;

    x(2) = -1;

end

for i=2:len

    if (v(i-1) == 1)

        x(k) = 1;

        if (v(i) ~= 1)

            x(k+1) = 1;

        else

            x(k+1) = -1;

        end

    else

        x(k) = -1;

        if (v(i) ~= 0)

            x(k+1) = -1;

        else

            x(k+1) = 1;

        end

    end

    k = k + 2;

end

if (v(len) == 0)

    x(2*len+1) = -1;

    x(2*len+2) = 0;

else

    x(2*len+1) = 1;

    x(2*len+2) = 0;

end

Код 2В1Q.

function x = B2Q1Cod(v)

len = length(v);

x = zeros(1, len/2);

i = 3;

k = 1;

while i <= len + 2

    if (v(i-2) == 0)

        if (v(i-1) == 0)

            x(k) = 2.1;

        else

            x(k) = 0.7;

        end

    else

        if (v(i-1) == 0)

            x(k) = -0.7;

        else

            x(k) = -2.1;

        end

    end

    i = i + 2;

    k = k + 1;

end

Файл-функция реализующая кодирование исходного сигнала тремя способами.

s = [1 0 1 0 0 0 1 1 0 1 1 1 0 1 1 0 0 1 1 1 0 0 0 0 1 1 1 0 0 0 1 1];

n = 0:32;

subplot(411)

stairs(n, [s 0]);

axis([0 32 -0.2 1.2]);

x1 = AmiCod(s);

subplot(412);

stairs(n, [x1 0]);

axis([0 32 -1.4 1.4]);

x2 = ManchesterCod(s);

subplot(413);

n = 0:0.5:33;

stairs(n, [x2 0]);

axis([0 33 -1.4 1.4]);

x3 = B2Q1Cod(s);

subplot(414);

n = 0:16;

stairs(n, [x3 0]);

axis([0 16 -2.5 2.5]);

2. Нахождение спектров исходного сигнала и сигнала, полученного после кодирования. Восстановление сигнала с помощью 20, 40, 80 гармоник, вычисление погрешности восстановления:

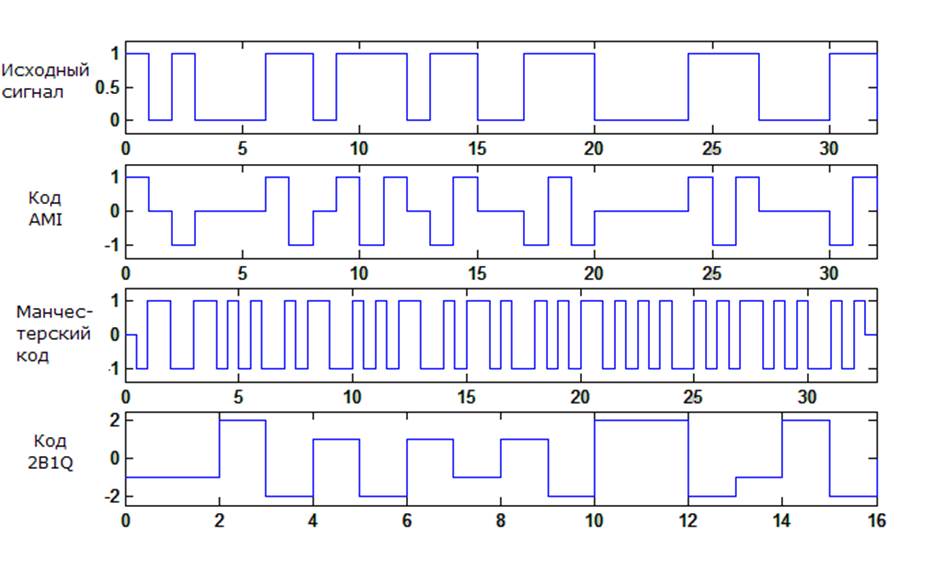
Нахождение спектров.

Нахождение коэффициентов Фурье для заданного сигнала.

function F = FourTrans(v)

T0 = length(v);

F = zeros(1, 100);

k = 0:99;

for i = 1:length(v)

    F = F + v(i)/T0*sinc(k/T0).*exp(-j*k*2*pi/T0*(i-0.5));

end

Коэффициенты Фурье для данного сигнала:

figure(2);

n = -99:99;

T0 = 32;

F1 = FourTrans(s);

subplot(411);

Fs1 = FourShift(F1);

stem(n/T0, abs(Fs1));

axis([-2 2 0 0.6])

F2 = FourTrans(x1);

subplot(412);

Fs2 = FourShift(F2);

stem(n/T0, abs(Fs2));

axis([-2 2 0 0.6])

F3 = FourTrans(x2);

subplot(413);

Fs3 = FourShift(F3);

stem(n/T0, abs(Fs3));

axis([-2 2 0 0.6])

F4 = FourTrans(x3);

subplot(414);

Fs4 = FourShift(F4);

n = -198:2:198;

T0 = 32;

stem(n/T0, abs(Fs4));

axis([-4 4 0 0.8])

Полученные амплитудные спектры, для исходного сигнала и сигналов, закодированных разными способами:

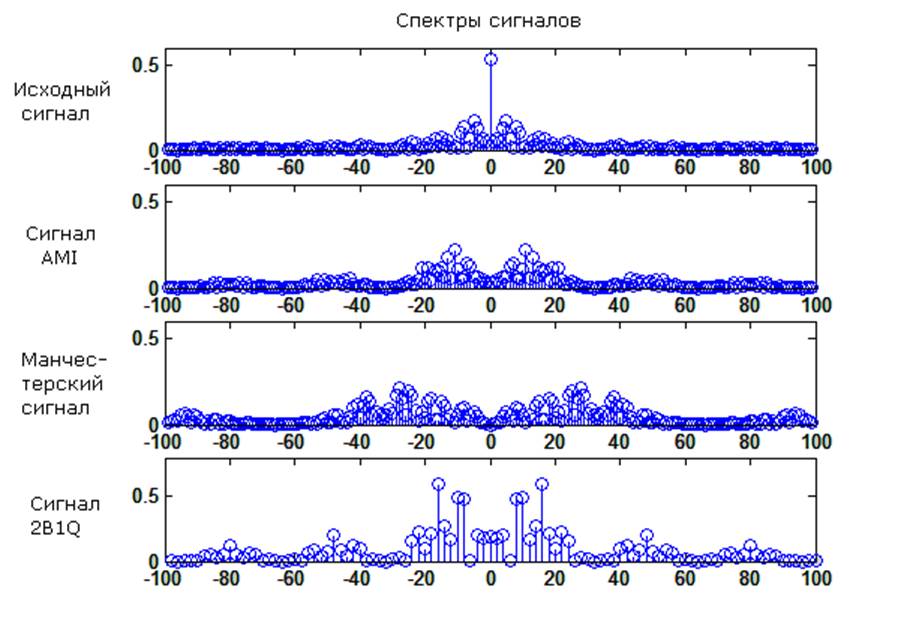
Восстановление сигнала.

     Функция реализующая восстановление сигнала 20, 40 и 80 гармониками:

n = 0:32;

subplot(411);

stairs(n, [s 0]);

axis([0 32 -0.2 1.2]);

n = 0:0.01:32;

y0 = CreateSignal(s, 100);

E0 = trapz(y0.^2);

y1 = vosst(F1, 20, n, 32);

dE1 = trapz((y0 - y1).^2)/E0*100

E1 = trapz(y1.^2);

subplot(412);

plot(n, y1);

axis([0 32 -0.2 1.2]);

y2 = vosst(F1, 40, n, 32);

dE2 = trapz((y0 - y2).^2)/E0*100

subplot(413);

plot(n, y2);

axis([0 32 -0.2 1.2]);

y3 = vosst(F1, 80, n, 32);

dE3 = trapz((y0 - y3).^2)/E0*100

subplot(414);

plot(n, y3);

axis([0 32 -0.2 1.2]);

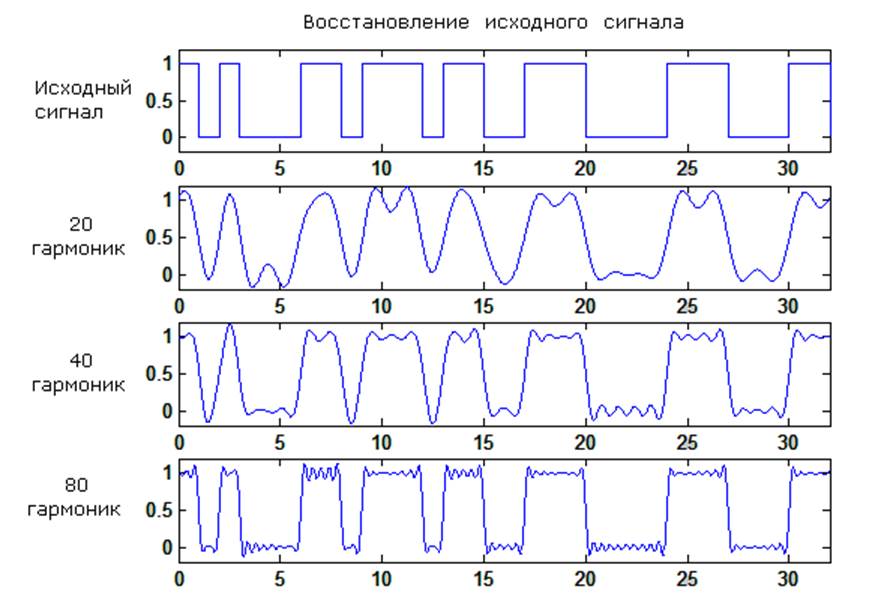
Нахождение погрешности при восстановлении:

 Энергия исходного сигнала:

      

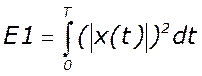
Погрешность восстановления:

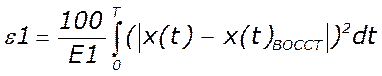
Погрешности при восстановлении 20,40 и 80 гармониками соответственно:

    dE1 = 6.2383 %

    dE2 = 3.7213 %

    dE3 = 1.6862 %

AMI.

Функция восстановления сигнала 20, 40, 80 гармониками:

n = 0:32;

subplot(411);

stairs(n, [x1 0]);

axis([0 32 -1.4 1.4]);

n = 0:0.01:32;

y0 = CreateSignal(x1, 100);

E0 = trapz(y0.^2);

y1 = vosst(F2, 20, n, 32);

dE1 = trapz((y0 - y1).^2)/E0*100

subplot(412);

plot(n, y1);

axis([0 32 -1.4 1.4]);

y2 = vosst(F2, 40, n, 32);

dE2 = trapz((y0 - y2).^2)/E0*100

subplot(413);

plot(n, y2);

axis([0 32 -1.4 1.4]);

y3 = vosst(F2, 80, n, 32);

dE3 = trapz((y0 - y3).^2)/E0*100

subplot(414);

plot(n, y3);

axis([0 32 -1.4 1.4]);

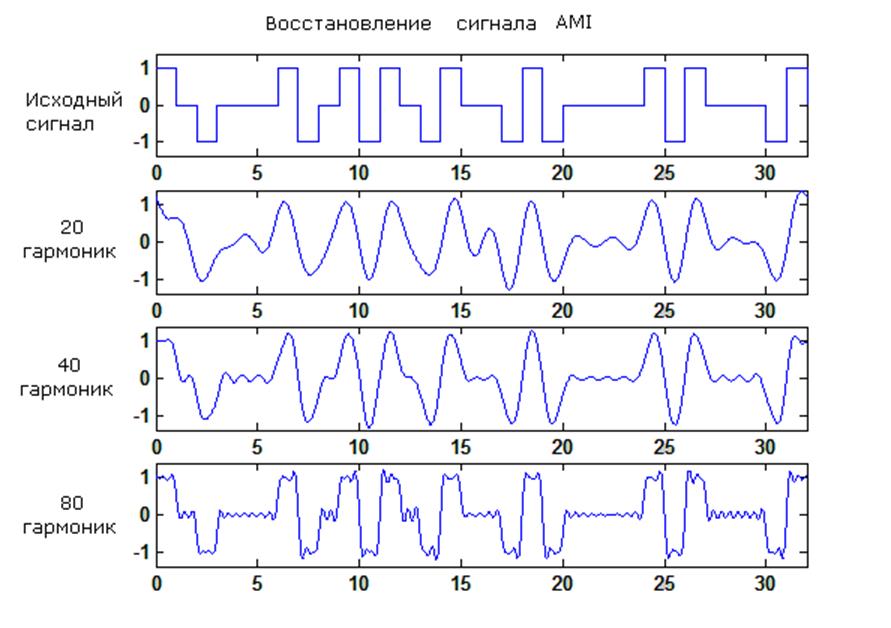
Погрешности при восстановлении 20,40 и 80 гармониками соответственно:

   dE1 =  22.0624 %

   dE2 =  13.7262 %

   dE3 =  6.1177 %

Манчестерский.

Функция восстановления сигнала 20, 40, 80 гармониками:

subplot(411);

n = 0:0.5:33;

stairs(n, [x2 0]);

axis([0 33 -1.4 1.4]);

n = 0:0.01:33;

y0 = CreateSignal(x2, 50);

E0 = trapz(y0.^2);

y1 = vosst(F3, 20, n, 33);

dE1 = trapz((y0 - y1).^2)/E0*100

subplot(412);

plot(n, y1);

axis([0 33 -1.4 1.4]);

y2 = vosst(F3, 40, n, 33);

dE2 = trapz((y0 - y2).^2)/E0*100

subplot(413);

plot(n, y2);

axis([0 33 -1.4 1.4]);

y3 = vosst(F3, 80, n, 33);

dE3 = trapz((y0 - y3).^2)/E0*100

subplot(414);

plot(n, y3);

axis([0 33 -1.4 1.4]);

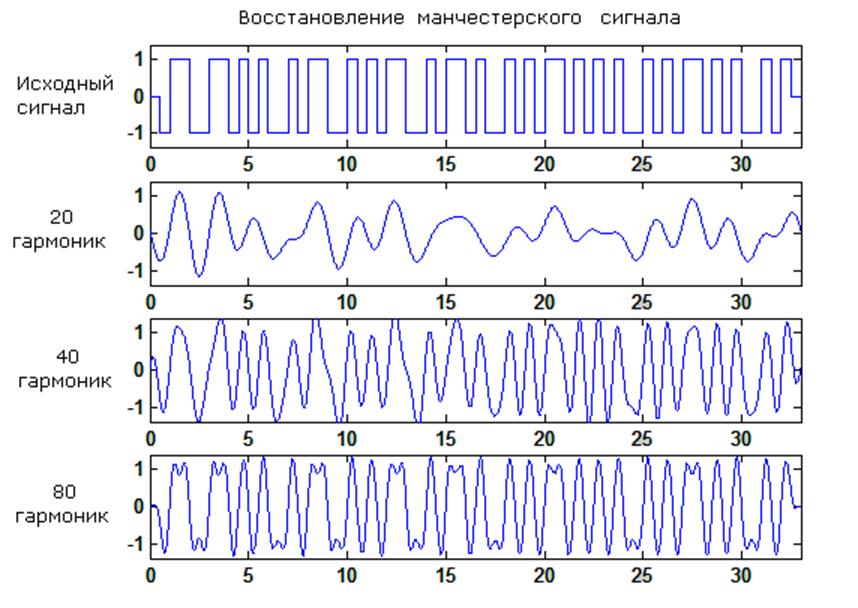
Погрешности при восстановлении 20,40 и 80 гармониками соответственно:

dE1 =  77.3580 %

dE2 =  22.6923 %

dE3 =  14.7991 %

2B1Q.

Функция восстановления сигнала 20, 40, 80 гармониками:

subplot(411);

n = 0:16;

stairs(n, [x3 0]);

axis([0 16 -2.5 2.5]);

n = 0:0.005:16;

y0 = CreateSignal(x3, 200);

E0 = trapz(y0.^2);

y1 = vosst(F4, 20, n, 16);

dE1 = trapz((y0 - y1).^2)/E0*100

subplot(412);

plot(n, y1);

axis([0 16 -2.5 2.5]);

y2 = vosst(F4, 40, n, 16);

dE2 = trapz((y0 - y2).^2)/E0*100

subplot(413);

plot(n, y2);

axis([0 16 -2.5 2.5]);

y3 = vosst(F4, 80, n, 16);

dE3 = trapz((y0 - y3).^2)/E0*100

subplot(414);

plot(n, y3);

axis([0 16 -2.5 2.5]);

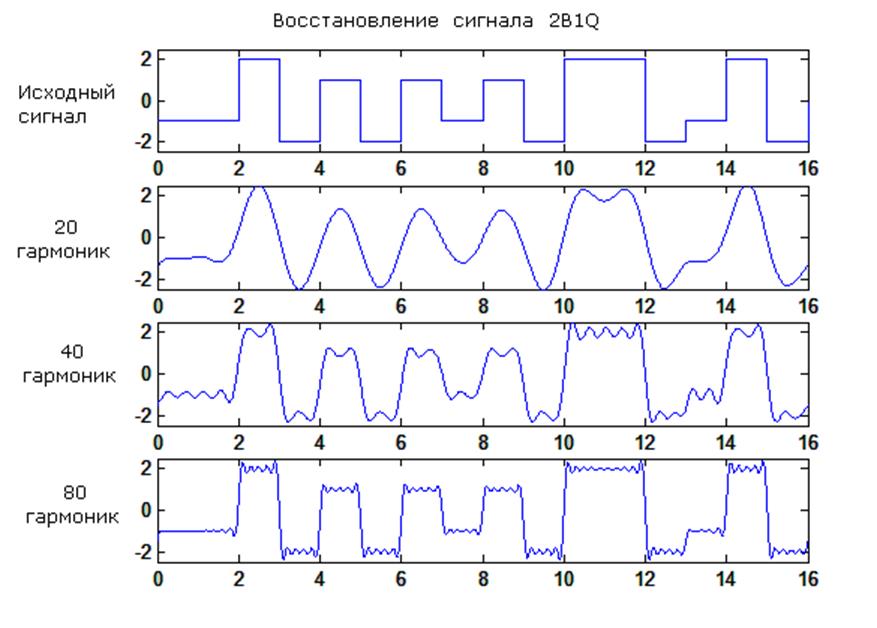
Погрешности при восстановлении 20,40 и 80 гармониками соответственно:

dE1 = 14.2775 %

dE2 =  6.6645 %

dE3 =  3.0323 %

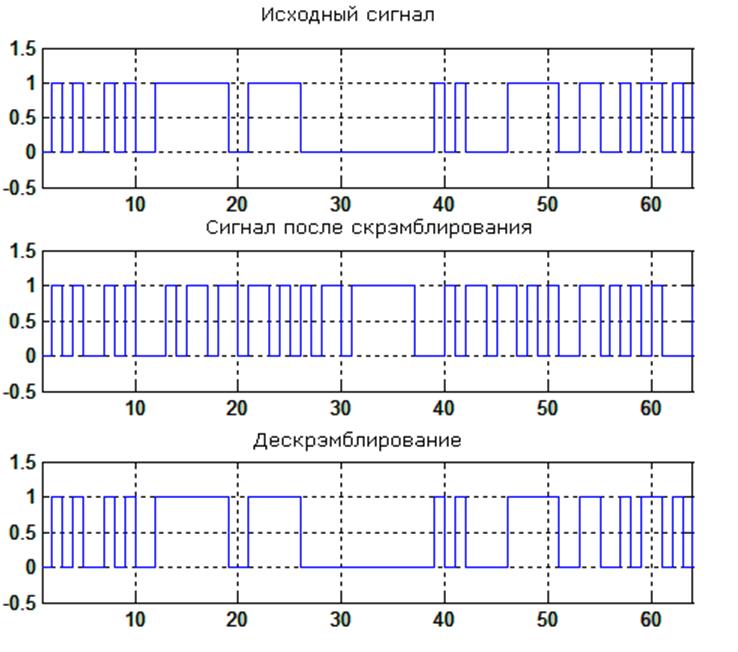
3. Скремблирование сигнала.

Скрэмблер  реализует следующее отношение: Bi = Ai * Bi-n * Bi-m

где В_i – двоичная цифра результирующего кода, полученного на i-м такте работы скрэмблера,  A_i  - двоичная цифра исходного кода поступающая на i-м такте на вход скрэмблера.

x = [0 1 0 1 0 0 1 0 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 1 1 1 1 1 0 0 1 1 0 0 1 0 1 1 0 1 0 1];

n=10;

m=31;

subplot(311)

stairs(x), grid

axis([1 64 -0.5 1.5]);

subplot(312)

% скрэмблирование

scr=zeros(1,64);

for i=1:64

    if i<=n

        scr(i)=x(i);

    elseif (i>n)&(i<=m)

        scr(i)=xor(x(i),scr(i-n));

    elseif i>m

        scr(i)=xor(xor(x(i),scr(i-n)),scr(i-m));

    end

end

stairs(scr), grid

axis([1 64 -0.5 1.5]);

subplot(313)

% дескрэмблирование

x2=zeros(1,64);

for i=1:64

    if i<=n

        x2(i)=scr(i);

    elseif (i>n)&(i<=m)

        x2(i)=xor(scr(i),scr(i-n));

    elseif i>m

        x2(i)=xor(xor(scr(i),scr(i-n)),scr(i-m));

    end

end

stairs(x2), grid

axis([1 64 -0.5 1.5]);