Кодирование сигналов. Генерация меандра и сигнала длиной 32 бит (NRZ). Спектры закодированных сигналов (сравнение с меандром)

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра ССОД

Лабораторная работа №1

по дисциплине «Информационные сети»

«Кодирование сигналов»

Факультет: АВТ                                                                                          Преподаватель:

Группа: АТ-93                                                                                             Моторин С.В.

Студент: Ахмедов А.Н.

                                                           Отметка о защите:

                                                                                                              ________________

    Дата защиты: «____»___________2012г.

Новосибирск, 2012

Содержание

1)  Генерация меандра и сигнала длиной 32 бит (NRZ).Его кодирование

 в AMI,  2B1Q и манчестерским кодом…………………………………………...3

2)  Спектры закодированных сигналов (сравнение с меандром)……………………6

3)  Восстановление сигналов………………………………………………………….9

4)  Скремблирование и дескремблирование………………………….……………..14

1)  Генерация меандра и сигнала длиной 32 бит (NRZ). Его кодирование в AMI,  2B1Q и манчестерским кодом.

% меандрическая последовательность

t=0:0.01:31;

d=0:2:31;

figure(1)

meandr=pulstran(t,d,'rectpuls',1);

subplot(111); plot(t*10^(-6),meandr);

axis([0 32*10^(-6) -0.5 1.5]);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('Меандрическая последовательность')

x=[1 1 0 1 0 1 1 1 1 0 1 0 1 0 0 0 0 1 1 1 0 1 0 0 1 0 1 0 1 0 1 0]

% Исходный сигнал

figure(2); subplot (211)

g=1:32;

stairs(10^(-6)*(g-1),x)% Исходный сигнал

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('Исходная последовательность');

axis([0 32*10^(-6) -1 2]); grid

% AMI код

prev=-1;

for i=1:32

    if x(i)==0

    m1(i)=-(prev); prev=m1(i);

    end

    if x(i)==1

    m1(i)=0;

    end

end

subplot (212)

g=1:32;

stairs(10^(-6)*(g-1),m1)%AMI код

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('AMI код');

axis([0 32*10^(-6) -2 2]); grid

% Манчестерский код

for i=1:32

    if x(i)==1

    m(2*i-1)=-1; m(2*i)=1;

    end

    if x(i)==0

    m(2*i-1)=1; m(2*i)=-1;

    end

end

for j=1:64

    M(j)=m(j);

end

% построим еще раз исходный сигнал

figure(3); subplot (311)

g=1:32;

stairs(10^(-6)*(g-1),x)% Исходный сигнал

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('Исходная последовательность');

axis([0 32*10^(-6) -1 2]); grid

subplot (312)

g=1:64;

stairs(10^(-6)*(g-1)/2,M)%Манчестерский код

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('Манчестерский код');

axis([0 32*10^(-6) -2 2]); grid

% код 2BQ1

for i=1:2:32

    if x(i)==1 & x(i+1)==1

    mn((i+1)/2)=-2.5;

    end

    if x(i)==1 & x(i+1)==0

    mn((i+1)/2)=-0.8;

    end

 if x(i)==0 & x(i+1)==1

    mn((i+1)/2)=2.5;

    end

    if x(i)==0 & x(i+1)==0

    mn((i+1)/2)=0.8;

    end

end

subplot (313)

g=0:15;

stairs(10^(-6)*g,mn);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('код 2BQ1');% код 2BQ1

axis([0 16*10^(-6) -3 3]);

xlabel('time,sec'); grid;

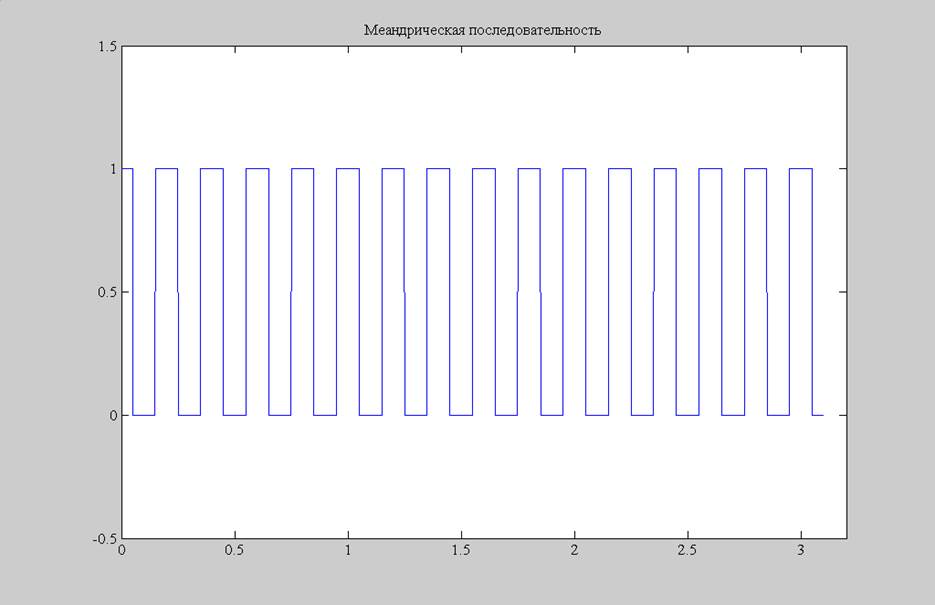
Рис.1. Меандрическая последовательность.

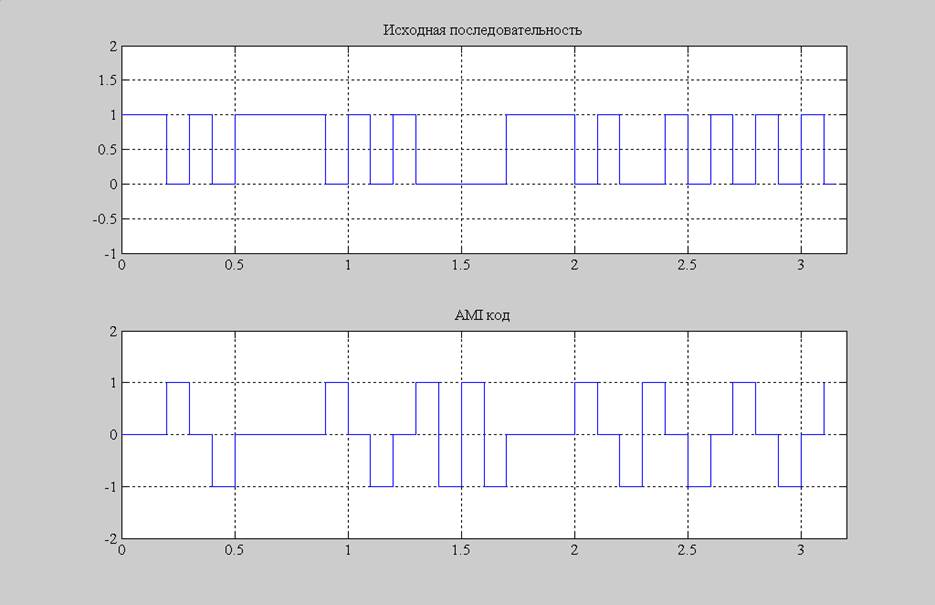
Рис.2. Исходный сигнал.AMI сигнал.

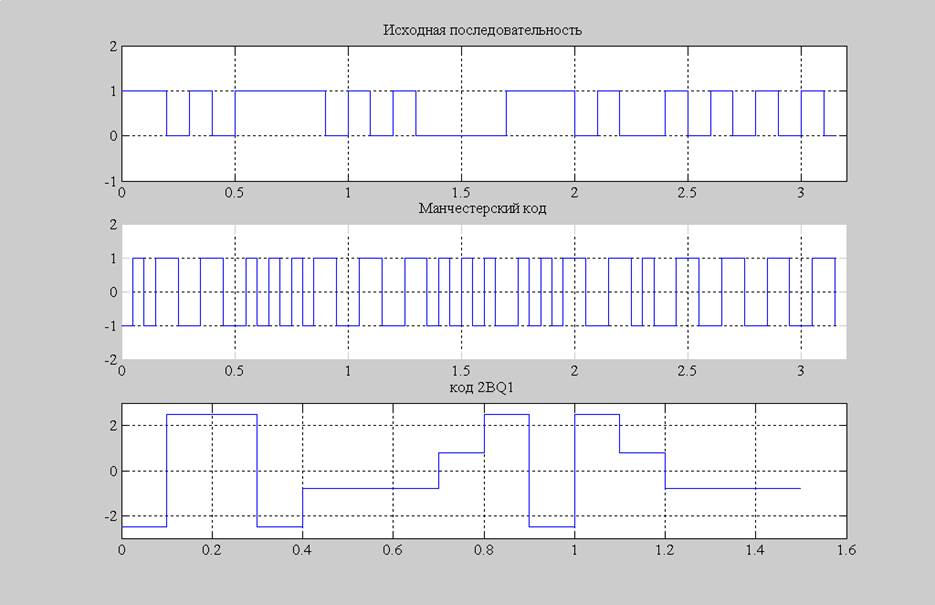
Рис.3 Исходный сигнал, манчестерский сигнал, 2BQ1 сигнал.

2)  Спектры закодированных сигналов (сравнение с меандром).

% спектр меандра

T=32*10^(-6);%длительность сигнала

Ts=T/128;% период отсчетов

Fmax=1/Ts;% Максимальная частота

df=1/T;%частотное разрешение

f1=-(Fmax-1)/2:df:(Fmax-1)/2;% частотная шкала

X1=fft(meandr,128);%вычисление ДПФ

X1_sh=fftshift(X1);%сдвиг ДПФ

figure(1);

subplot(311);

stem(f1,abs(X1_sh));% спектр меандра

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('Спектр меандра');

%получение спектра исходного сигнала

Tc=32*10^(-6);%длительность сигнала

Tsc=T/128;% период отсчетов

Fmaxc=1/Tsc;%

dfc=1/Tc;

f1c=-(Fmaxc-1)/2:dfc:(Fmaxc-1)/2;% частотная шкала

X1c=fft(x, 128);

spec_NRZ =fftshift(X1c);

subplot(312);

stem(f1c,abs(spec_NRZ));% спектр сигнала NRZ

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('Спектр сигнала');

%получение спектра AMI кода

T_m1=32*10^(-6);%длительность сигнала в манчестерском коде

Ts_m1=T_m1/128;

Fmax_m1=1/Ts_m1;

df_m1=1/T_m1;

f1_m1=-(Fmax_m1-1)/2:df_m1:(Fmax_m1-1)/2;% частотная шкала

X1_m1=fft(m1, 128);

spec_AMI =fftshift(X1_m1);

subplot(313);

stem(f1_m1,abs(spec_AMI));% спектр сигнала AMI

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('Спектр сигнала в AMI коде');

figure(2);

subplot(311);

stem(f1,abs(X1_sh));% спектр меандра

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('Спектр меандра');

%получение спектра манчестерского кода

T_M=32*10^(-6);%длительность сигнала в манчестерском коде

Ts_M=T_M/128;%

Fmax_M=1/Ts_M;

df_M=1/T_M;

f1_M=-(Fmax_M-1)/2:df_M:(Fmax_M-1)/2;% частотная шкала

X1_M=fft(M, 128);

spec_Manch=fftshift(X1_M);

subplot(312);

stem(f1_M,abs(spec_Manch));% спектр сигнала в манчестере

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('Спектр сигнала в манчестерском коде');

%получение спектра 2B1Q кода

T_mn=16*10^(-6);%длительность сигнала

Ts_mn=T_mn/128;% период отсчетов

Fmax_mn=1/Ts_mn;

df_mn=1/T_mn;

f1_mn=-(Fmax_mn-1)/2:df_mn:(Fmax_mn-1)/2; % частотная шкала

X1_mn=fft(mn, 128);

spec_2B1Q=fftshift(X1_mn);

subplot(313);

stem(f1_mn,abs(spec_2B1Q));% спектр 2B1Q кода

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('Спектр 2B1Q кода');

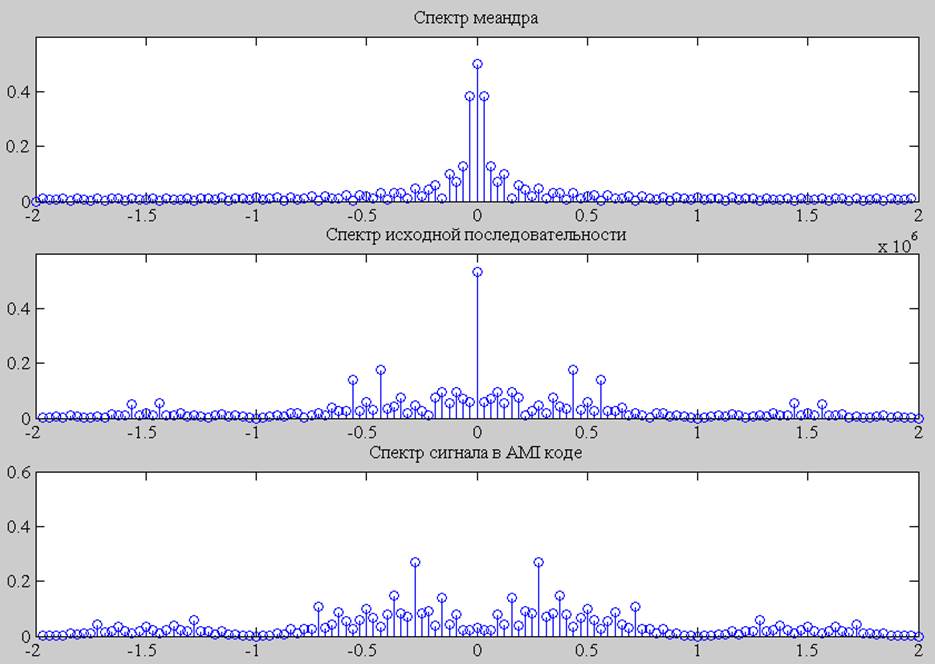
Рис.4. Спектры сигналов.

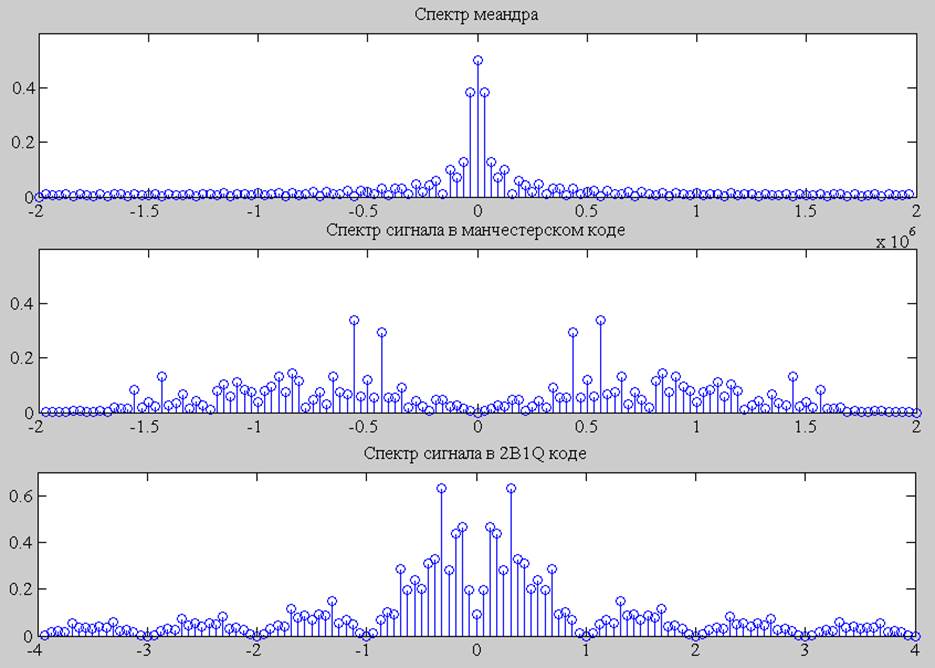
Рис.5 Спектры сигналов.

3)  Восстановление сигналов

Нахождение погрешности при восстановлении из спектра:

%восстановление исходного сигнала

n = 0:32;

subplot(411);

stairs(n, [x 0]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Исходный сигнал в AMI коде');

axis([0 32 -2 2]);

n = 0:0.01:32;

E0 = trapz(z0.^2);

z1 = recover(spec_NRZ, 3, n, 32);

pogresh1 = trapz((z0 - z1).^2)/E0*100

subplot(412);

plot(n, z1);

axis([0 32 -2 2]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Восстановленный сигнал по 3 гармоникам');