Информатика и выч. техника \ Информационные сети

Кодирование сигналов. Генерация меандра и сигнала длиной 32 бит (NRZ). Спектры закодированных сигналов (сравнение с меандром), страница 2

z2 = recover(spec_NRZ, 5, n, 32);

pogresh 2 = trapz((z0 - z2).^2)/E0*100

subplot(413);

plot(n, z2);

axis([0 32 -2 2]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Восстановленный сигнал по 5 гармоникам');

z3 = recover(spec_NRZ, 7, n, 32);

pogresh3 = trapz((z0 - z3).^2)/E0*100

subplot(414);

plot(n, z3);

axis([0 32 -2 2]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Восстановленный сигнал по 7 гармоникам');

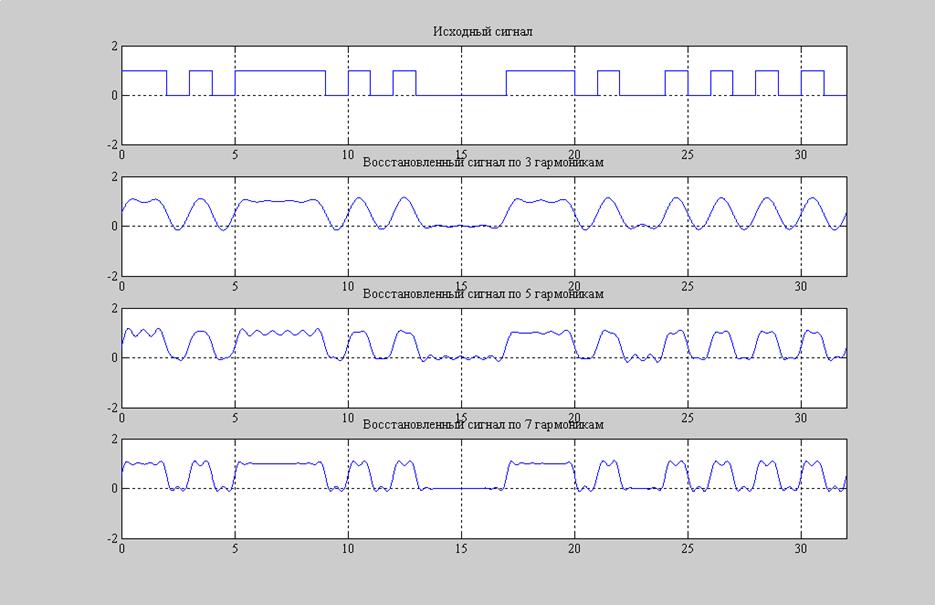
Рис.6 Восстановление исходного сигнала  по 3,5,7 гармоникам.

pogresh1 = 6.2178 % погрешность от восстановления 3 гармониками

pogresh2 = 4.4225 % погрешность от восстановления 5 гармониками

pogresh3 = 3.2058 % погрешность от восстановления 7 гармониками

%восстановление сигнала в AMI коде

n = 0:32;

subplot(411);

stairs(n, [m1 0]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Исходный сигнал в AMI коде');

axis([0 32 -2 2]);

n = 0:0.01:32;

E0 = trapz(z0.^2);

z1 = recover(spec_AMI, 3, n, 32);

pogresh1 = trapz((z0 - z1).^2)/E0*100

subplot(412);

plot(n, z1);

axis([0 32 -2 2]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Восстановленный сигнал по 3 гармоникам');

z2 = recover(spec_AMI, 5, n, 32);

pogresh 2 = trapz((z0 - z2).^2)/E0*100

subplot(413);

plot(n, z2);

axis([0 32 -2 2]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Восстановленный сигнал по 5 гармоникам');

z3 = recover(spec_AMI, 7, n, 32);

pogresh3 = trapz((z0 - z3).^2)/E0*100

subplot(414);

plot(n, z3);

axis([0 32 -2 2]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Восстановленный сигнал по 7 гармоникам');

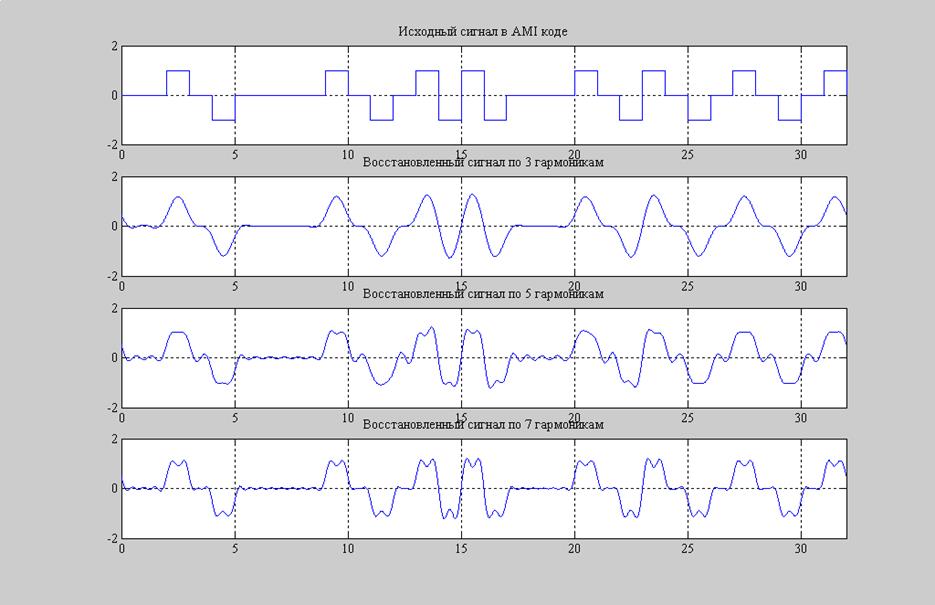
Рис.7. Восстановление AMI  сигнала по 3,5,7 гармоникам.

pogresh1 = 12.3222 % погрешность от восстановления 3 гармониками

pogresh2 = 8.2858 % погрешность от восстановления 5 гармониками

pogresh3 = 6.3064 % погрешность от восстановления 7 гармониками

%восстановление сигнала в манчестерском коде

n = 0:0.5:32;

subplot(411);

stairs(n, [M 0]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Исходный сигнал в AMI коде');

axis([0 32 -2 2]);

n = 0:0.005:32;

E0 = trapz(z0.^2);

z1 = recover(spec_Manch, 3, n, 32);

pogresh1 = trapz((z0 - z1).^2)/E0*100

subplot(412);

plot(n, z1);

axis([0 32 -2 2]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Восстановленный сигнал по 3 гармоникам');

z2 = recover(spec_Manch, 5, n, 32);

pogresh 2 = trapz((z0 - z2).^2)/E0*100

subplot(413);

plot(n, z2);

axis([0 32 -2 2]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Восстановленный сигнал по 5 гармоникам');

z3 = recover(spec_Manch, 7, n, 32);

pogresh3 = trapz((z0 - z3).^2)/E0*100

subplot(414);

plot(n, z3);

axis([0 32 -2 2]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Восстановленный сигнал по 7 гармоникам');

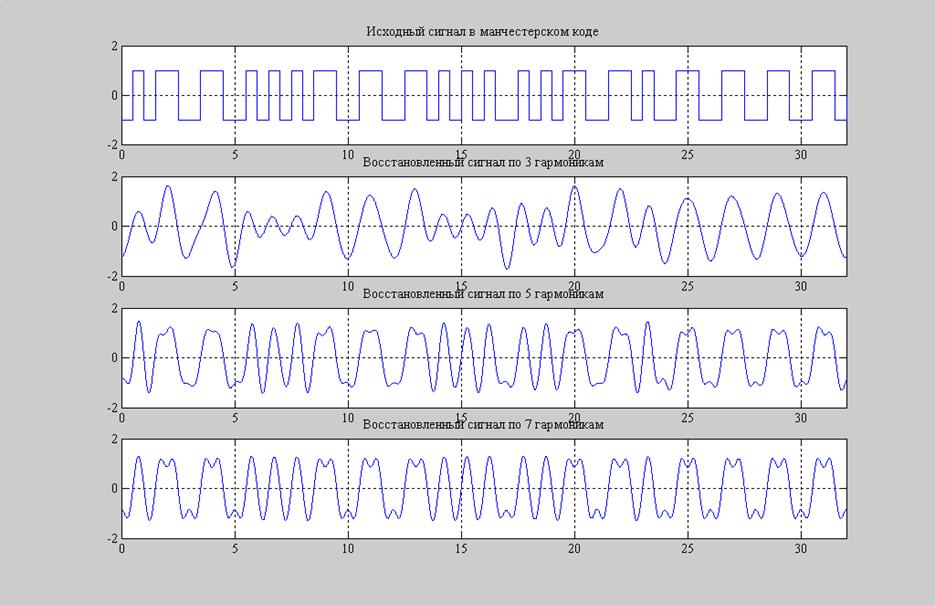
Рис.8 Восстановление манчестерского сигнала по 3,5,7 гармоникам.

pogresh1 = 32.5336 % погрешность от восстановления 3 гармониками

pogresh2 = 14.2699 % погрешность от восстановления 5 гармониками

pogresh3 = 12.7568 % погрешность от восстановления 7 гармониками

%восстановление сигнала в 2B1Q коде

n = 0:16;

subplot(411);

stairs(n, [M 0]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Исходный сигнал в AMI коде');

axis([0 16 -3 3]);

n = 0:0.005:16;

E0 = trapz(z0.^2);

z1 = recover(spec_2B1Q, 3, n, 16);

pogresh1 = trapz((z0 - z1).^2)/E0*100

subplot(412);

plot(n, z1);

axis([0 16 -3 3]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Восстановленный сигнал по 3 гармоникам');

z2 = recover(spec_2B1Q, 5, n, 16);

pogresh 2 = trapz((z0 - z2).^2)/E0*100

subplot(413);

plot(n, z2);

axis([0 16 -3 3]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Восстановленный сигнал по 5 гармоникам');

z3 = recover(spec_2B1Q, 7, n, 16);

pogresh3 = trapz((z0 - z3).^2)/E0*100

subplot(414);

plot(n, z3);

axis([0 16 -3 3]);grid;

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,11),

title('Восстановленный сигнал по 7 гармоникам');

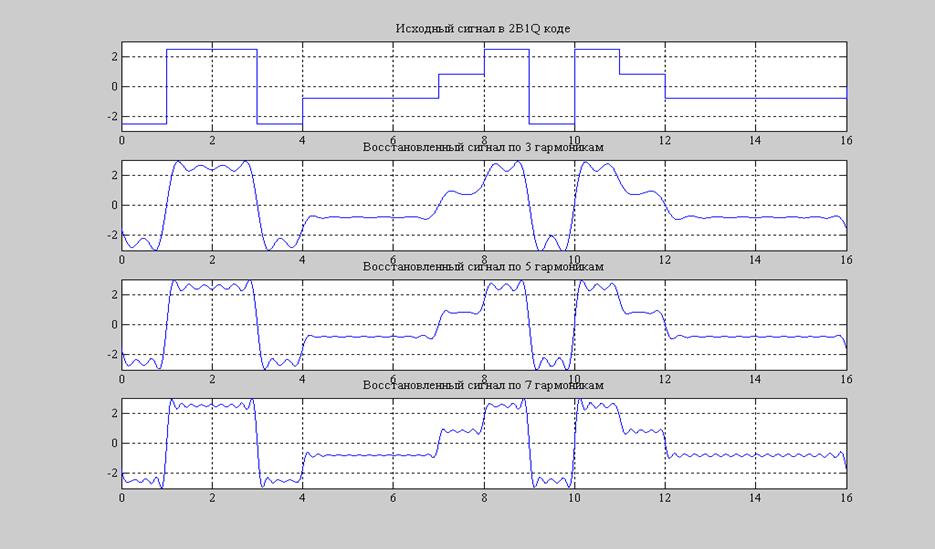
Рис.9. Восстановление 2BQ1 сигнала по 3,5,7 гармоникам.

pogresh1 = 5.9783 % погрешность от восстановления 3 гармониками

pogresh2 = 3.9732 % погрешность от восстановления 5 гармониками

pogresh3 = 2.8069 % погрешность от восстановления 7 гармониками

4)  Скремблирование и дескремблирование

x = [1 0 1 1 0 0 0 0 1 1 1 1 1 1 1 1 1 1 0 0 1 1 0 0 1 0 1 1 1 1 1 1 0 1 1 1 0 0 1 0 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 1 1 0 1 0 1];

n=5;

m=23;

subplot(311)

stairs(x), grid

axis([1 64 -0.5 1.5]);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('Исходная последовательность');

subplot(312)

% скремблирование

scr=zeros(1,64);

for i=1:64

    if i<=n

        scr(i)=x(i);

    elseif (i>n)&(i<=m)

        scr(i)=xor(x(i),scr(i-n));

    elseif i>m

        scr(i)=xor(xor(x(i),scr(i-n)),scr(i-m));

    end

end

stairs(scr), grid

axis([1 64 -0.5 1.5]);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('Скремблированная последовательность');

subplot(313)

% дескремблирование

x2=zeros(1,64);

for i=1:64

    if i<=n

        x2(i)=scr(i);

    elseif (i>n)&(i<=m)

        x2(i)=xor(scr(i),scr(i-n));

    elseif i>m

        x2(i)=xor(xor(scr(i),scr(i-n)),scr(i-m));

    end

end

stairs(x2), grid

axis([1 64 -0.5 1.5]);

set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),

title('Дескремблированная последовательность');

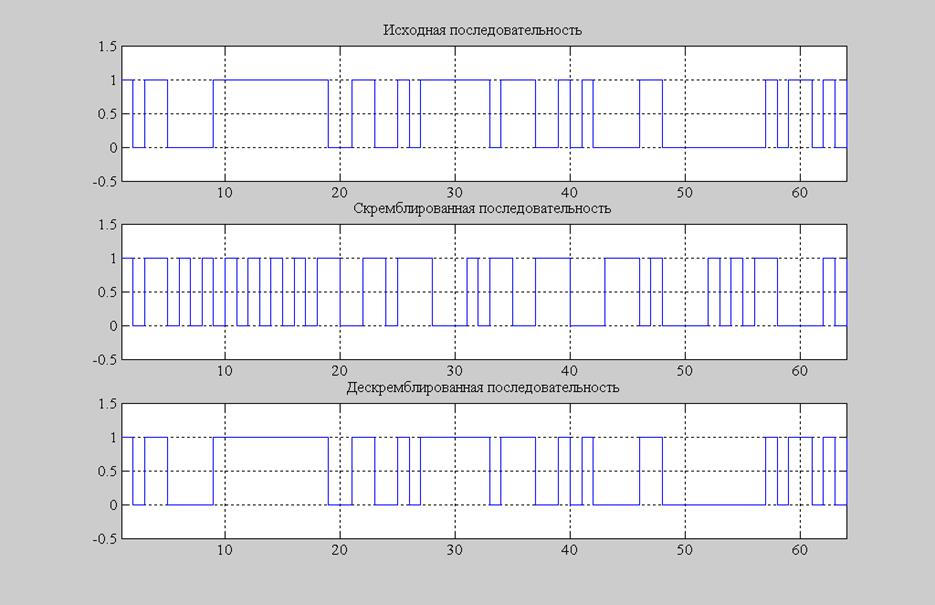
Рис.10. Скремблирование и дескремблирование сигнала.

Скремблирование используется для борьбы с большими последовательностями нулей и единиц, а так же для шифрования.

 - для данного случая.
Здесь  - двоичная цифра результирующего кода, полученная на i-м такте работы скремблера. - двоичная цифра исходного кода, поступающая на i-м такте на вход скремблера. и  - двоичные цифры результирующего кода, полученные на предыдущих тактах работы скремблера, соответственно на 5 и на 23 тактов ранее текущего такта, и объединенные операцией сложение по модулю 2. Различие между алгоритмами скремблирования заключается в изменении номеров тактов (т.е. 5 и 23 в данном случае).

Скачать файл