Новосибирский Государственный Технический Университет
Факультет Автоматики и Вычислительной Техники
Кафедра ССОД
Дисциплина «Информационные сети»
Лабораторная работа № 1
КОДИРОВАНИЕ СИГНАЛОВ
Выполнил: Преподаватель:
Спитченко В. М. проф. Моторин С.В.
Группа: АИ-72
Новосибирск
2010
1. Исходный сигнал
Введем некоторые данные об исходном сигнале:
1) частота сигнала
![]() рад/c
рад/c
2) период сигнала
![]() c
c
3) длительность импульса
![]() c
c
Исходная последовательность битов:
1000 1101 0111 0100 1010 1010 1100 0110
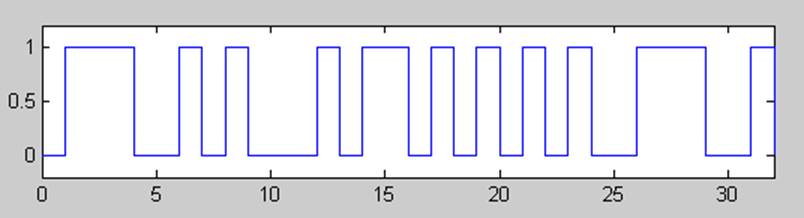
Рис.1. Исходный сигнал NRZ.
Генерирование кода AMI:
function x = AmiCod(v)
len = length(v);
x = zeros(1, len);
odd = 0;
for i = 1:len
if (v(i) == 1)
if (odd == 0)
x(i) = 1;
odd = 1;
else
x(i) = -1;
odd = 0;
end
else
x(i) = 0;
end
end
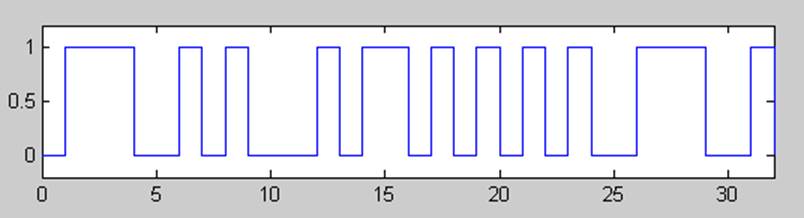
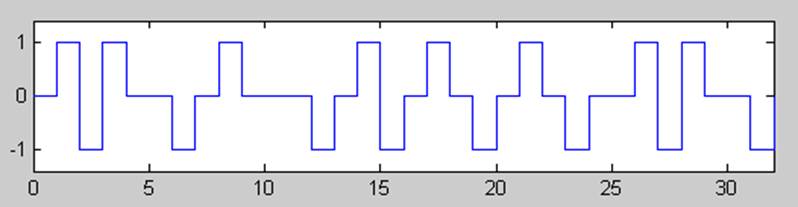
Рис.2. AMI
Генерирование Манчестерского кода:
function x = AmiCod(v)
len = length(v);
x = zeros(1, len);
odd = 0;
for i = 1:len
if (v(i) == 1)
if (odd == 0)
x(i) = 1;
odd = 1;
else
x(i) = -1;
odd = 0;
end
else
x(i) = 0;
end
end

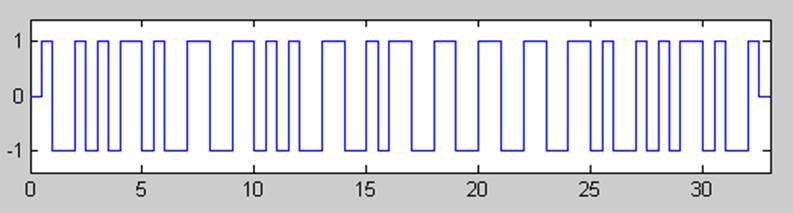
Рис.2. Манчестерский код.
Генерирование кода 2B1Q:
function x = B2Q1Cod(v)
len = length(v);
x = zeros(1, len/2);
i = 3;
k = 1;
while i <= len + 2
if (v(i-2) == 0)
if (v(i-1) == 0)
x(k) = 2.1;
else
x(k) = 0.7;
end
else
if (v(i-1) == 0)
x(k) = -0.7;
else
x(k) = -2.1;
end
end
i = i + 2;
k = k + 1;
end

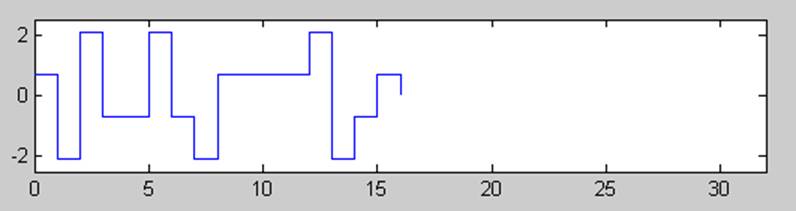
Рис.3. 2B1Q
2. Восстановление сигнала по 3, 5, 7 гармоникам
t1=0:0.01:31;% меандр
d=0:2:31;
figure(1)
meandr=pulstran(t1,d,'rectpuls',1);
w0 = pi*10^6; T=2*pi/w0;
t = 0:T/1000:16*T;
c0 = 1/2;
x = c0*ones(1,length(t));% постоянная составляющая
for n=1:3,%восстановление по 3 гармоникам
cn = 1/pi/n*sin(pi*n/2);
c_n=conj(cn);
x = x + cn*exp(j*n*w0*t) + c_n*exp(-j*n*w0*t);
end
subplot(311);
plot(t1*10^(-6),meandr,'k', t,x);
grid; axis ([0 0.5*10^(-5) -0.5 1.5])
x1 = c0*ones(1,length(t));
for n1=1:5,%восстановление по 5 гармоникам
cn1 = 1/pi/n1*sin(pi*n1/2);
c_n1=conj(cn1);
x1 = x1 + cn1*exp(j*n1*w0*t) + c_n1*exp(-j*n1*w0*t);
end
subplot(312);
plot(t1*10^(-6),meandr,'k', t,x1, 'c');
grid; axis ([0 0.5*10^(-5) -0.5 1.5])
x2 = c0*ones(1,length(t));
for n2=1:7,%восстановление по 7 гармоникам
cn2 = 1/pi/n2*sin(pi*n2/2);
c_n2=conj(cn2);
x2 = x2 + cn2*exp(j*n2*w0*t) + c_n2*exp(-j*n2*w0*t);
end
subplot(313);
plot(t1*10^(-6),meandr,'k', t,x2, 'red');
grid; axis ([0 0.5*10^(-5) -0.5 1.5])
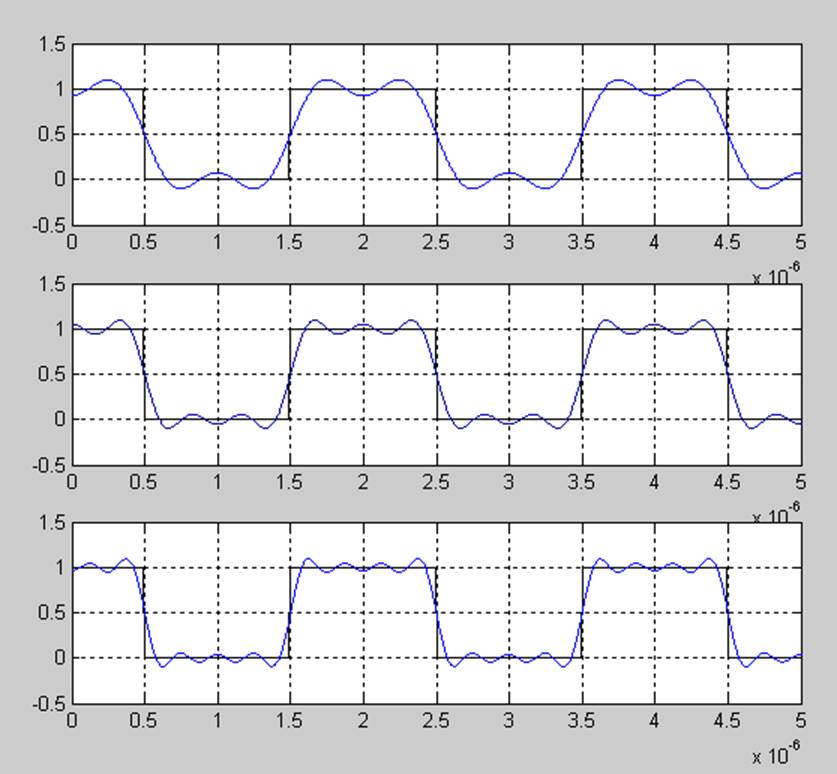
Рис.4. Восстановление сигнала 1)по трем гармоникам
2) по пяти гармоникам
3) по семи гармоникам
3. Скремблирование
Скремблирование заключается в побитном вычислении результирующего кода на основании битов исходного кода и полученных в предыдущих тактах битов результирующего кода. В данном случае скремблер работает на основе выражения:
Bi=AÅI Bi-3 ÅBi-5
ii=1:32;
y=[0 1 1 1 0 0 1 0 1 0 0 0 1 0 1 1 0 1 0 1 0 1 0 1 0 0 1 1 1 0 0 1];
for i=1:3
scr(i)=y(i);
end
for i=4:5
scr(i)=xor (y(i),scr(i-3));
end
for i=6:32
scr1(i)=xor(y(i),scr(i-3));
scr(i)=xor(scr1(i),scr(i-5));
end
figure(1)
subplot(311)
stairs(ii,y);
axis([0 32 -1 2]);
title('Исходный сигнал');% исходный сигнал
subplot(312)
stairs(ii,scr);
axis([0 32 -1 2]); %скремблированный сигнал
title('Скремблированный сигнал');
%восстановление скремблированного сигнала
for i=1:3
Y(i)=scr(i);
end
for i=4:5
Y(i)=xor (scr(i),scr(i-3));
end
for i=6:32
Y1(i)=xor(scr(i),scr(i-3));
Y(i)=xor(Y1(i),scr(i-5));
end
subplot(313)
stairs(ii,Y);
axis([0 32 -1 2]); %восстановленный сигнал
title('Восстановленный сигнал');
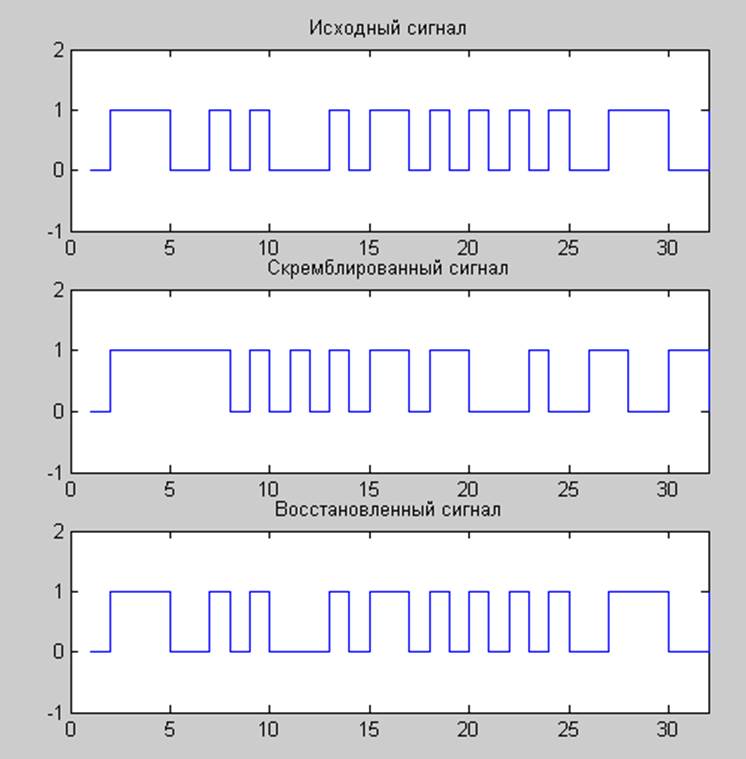
Рис.5.Скремблирование сигнала.
2. Получение спектров сигнала в различных кодах
Нахождение спектров.
% спектр меандра
t=0:0.01:31;
d=0:2:31;
meandr=pulstran(t,d,'rectpuls',1);
T=32*10^(-6);%длительность сигнала
Ts=T/128;% период отсчетов
Fmax=1/Ts;% Максимальная частота
df=1/T;%частотное разрешение
f1=-(Fmax-1)/2:df:(Fmax-1)/2;% частотная шкала
X1=fft(meandr,128);%вычисление ДПФ
X1_sh=fftshift(X1);%сдвиг ДПФ
figure(1);
subplot(311);
stem(f1,abs(X1_sh));% спектр меандра
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
title('Спектр меандра');
%получение спектра AMI кода
T_m1=32*10^(-6);%длительность сигнала в манчестерском коде
Ts_m1=T_m1/128;
Fmax_m1=1/Ts_m1;
df_m1=1/T_m1;
f1_m1=-(Fmax_m1-1)/2:df_m1:(Fmax_m1-1)/2;% частотная шкала
X1_m1=fft(m1, 128);
spec_AMI =fftshift(X1_m1);
subplot(313);
stem(f1_m1,abs(spec_AMI));% спектр сигнала AMI
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
title('Спектр сигнала в AMI коде');
%получение спектра манчестерского кода
T_M=32*10^(-6);%длительность сигнала в манчестерском коде
Ts_M=T_M/128;%
Fmax_M=1/Ts_M;
df_M=1/T_M;
f1_M=-(Fmax_M-1)/2:df_M:(Fmax_M-1)/2;% частотная шкала
X1_M=fft(M, 128);
spec_Manch=fftshift(X1_M);
subplot(312);
stem(f1_M,abs(spec_Manch));% спектр сигнала в манчестере
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
title('Манчестерский код');
%получение спектра 2B1Q кода
T_mn=16*10^(-6);%длительность сигнала
Ts_mn=T_mn/128;% период отсчетов
Fmax_mn=1/Ts_mn;
df_mn=1/T_mn;
f1_mn=-(Fmax_mn-1)/2:df_mn:(Fmax_mn-1)/2; % частотная шкала
X1_mn=fft(mn, 128);
spec_2B1Q=fftshift(X1_mn);
subplot(313);
stem(f1_mn,abs(spec_2B1Q));% спектр 2B1Q кода
set(gca, 'FontName', 'Times New Roman Cyr', 'FontSize' ,12),
ylabel('2B1Q');
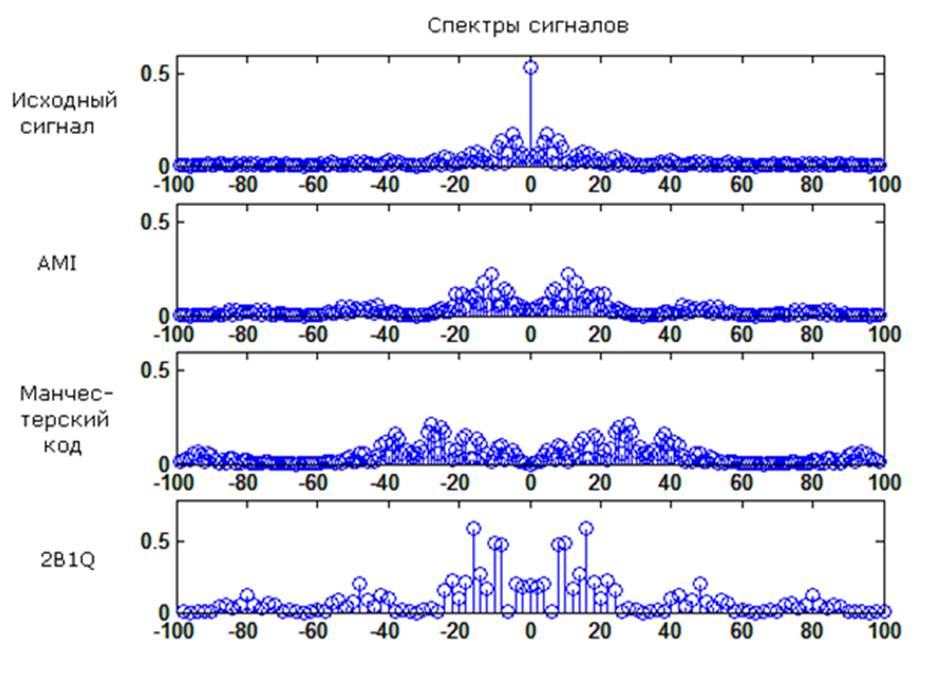
Полученные амплитудные спектры, для исходного сигнала и сигналов, закодированных разными способами:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.