Отсчёты соединяются прямыми линиями. При одинаковом количестве отсчётов данный способ экстраполяции даёт более точный результат, чем восстановления сигнала с помощью интерполяционного полинома нулевого порядка.
Файл-сценарий Matlab для генерирования восстановления сигнала с помощью интерполяционного полинома нулевого порядка и ФНЧ (Приложение 4 Процедура 4.4. методического указания):
% Программа демонстрации восстановления сигнала
% с помощью интерполяционного полинома нулевого порядка и ФНЧ,
% используемого для сглаживания восстановленного сигнала
t=-3:0.01:7; % задание интервала времени
n=-3:7; % номера отсчетов сигнала
s=[0 0 2.5 6.4 3 4.2 1 -2.5 0 -1 0]; % дискретный сигнал
d=[n' s']; % параметры для функции pulstran
% сигнал,восстановленный полиномом нулевого порядка
y=pulstran(t,d,'rectpuls');
% фильтрация восстановленного сигнала
[b,a]=butter(6,2*pi*0.5,'s'); % получение
характеристик фильтра
% Баттерворта
lsim(b,a,y,t); % фильтрация и построение графика после фильтрации
hold on; axis([-3,8,-4,8])
plot(n, s,'o', t, y) % график восстановленного сигнала
hold on
% сигнал,восстановленный интерполятором sinc
y1=pulstran(t,d,'sinc');
plot(t, y1,'-.m'); grid on
% построение графиков отдельных прямоугольных импульсов
for k=1:length(s),plot(t,s(k)*rectpuls(t-n(k)), ':'),
end
hold off
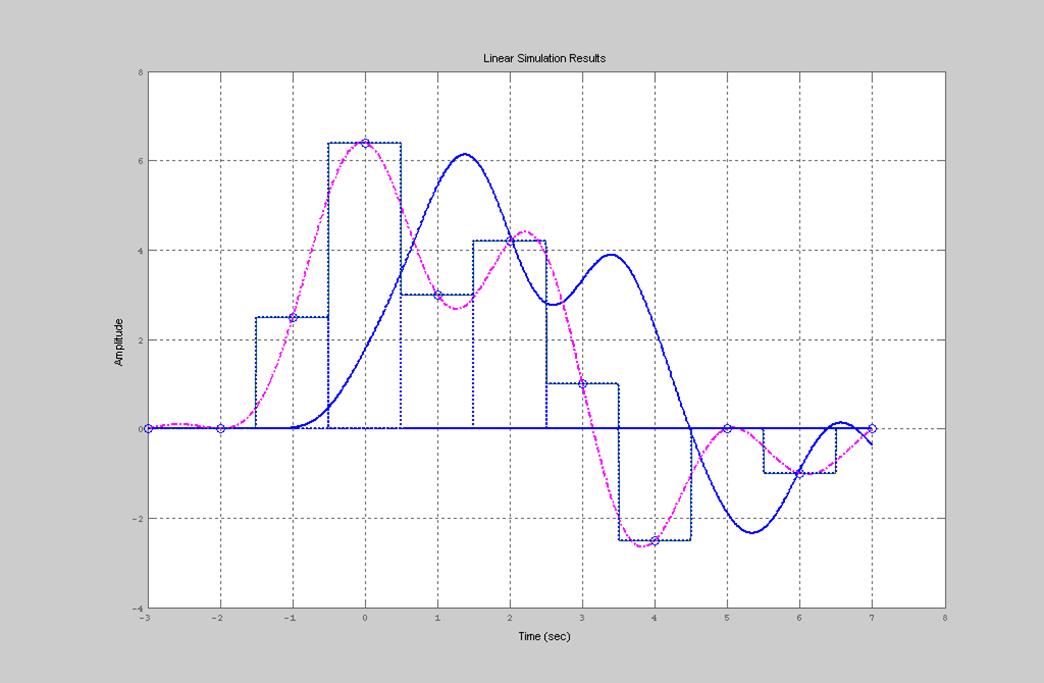
Рис. 14. Графики восстановления сигнала с помощью интерполяционного полинома нулевого порядка и ФНЧ, используемого для сглаживания восстановленного сигнала
В результате выполнения программы (рис. 14.) видно, что восстановление сигнала с помощью интерполяционного полинома нулевого порядка и сглаживания с помощью ФНЧ позволяет исключить проблему, связанную с подбором числа отсчетов при восстановлении. Используемый в качестве сглаживающего ФНЧ, фильтр Баттерворта 6 порядка не пропускает гармоники с частотами, превышающими частоту среза 0.5 Гц. Темсамым достигается устранение«лишней ступенчатости» (гармоник с амплитудами, не соответствующими значениям амплитуд исходного сигнала в каждой точке).
Мы рассмотрели четыре способа восстановления сигнала по его отсчётам. Первый способ (использование идеального ФНЧ) дал более точный результат, чем три других. Сигнал, полученный при помощи интерполяционного полинома нулевого порядка, дал наихудший результат.
Задание №5:Создание и выполните в пакете Simulink модели дискретизации и восстановления синусоидального сигнала.
Расчет числителя и знаменателя передаточной функции TransferFcn с помощью фильтра Баттерворта 10 порядка:
Параметры исходного синусоидального сигнала: Частота 10 Гц, единичная амплитуда (A = 1)
[b,a]=butter(10,2*pi*10,'s')
Описание функции:
Функция butter позволяет синтезировать аналоговые и дискретные фильтры Баттерворта нижних частот, верхних частот, полосовые и режекторные. Фильтры Баттерворта характеризуются амплитудно-частотной характеристикой, максимально плоской в полосе пропускания и монотонно спадающей за ее пределами.
[b,a] = butter(n,Wn,'s')
Производит синтез аналогового фильтра Баттерворта n-го порядка, имеющего АЧХ фильтра нижних частот и круговую частоту среза, равную Wn рад/с. Функция возвращает описание фильтра в виде векторов-строк b и a, имеющих длину n+1 и содержащих коэффициенты полиномов числителя и знаменателя функции передачи в порядке убывания степеней переменной s:
Значение круговой частоты среза Wn должно быть положительным.
Если параметр Wn является двухэлементным вектором, Wn = [w1 w2], вызов функции butter(n,Wn,'s') производит синтез аналогового полосового фильтра порядка 2*n, полоса пропускания которого лежит в пределах от w1 до w2.
Результат расчета фильтра Баттерворта:
b = 0 0 0 0 0 0 0 0 0 0 9.5896e+017
a = 1 401.65 80661 1.0617e+007 1.0112e+009 7.2694e+010 3.9921e+012
1.6547e+014 4.963e+015 9.7563e+016 9.5896e+017
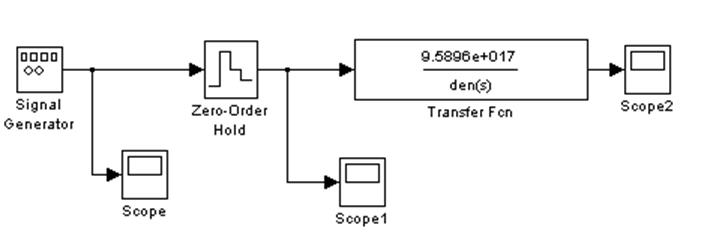
Рис. 15. Модель дискретизации и восстановления синусоидального сигнала.
Результаты моделирования:
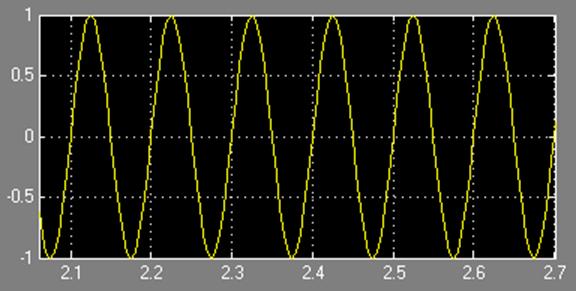
Рис. 16. Исходный дискретизируемый синусоидальный сигнал с частотой 10 Гц, полученный с выхода генератора сигналов.
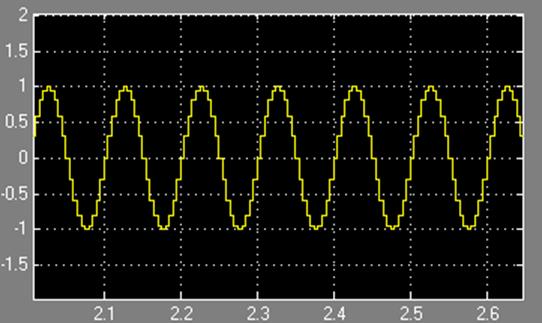
Рис. 17. Сигнал, полученный с выхода экстраполятора нулевого порядка, с тактом дискретности 0.005 сек.
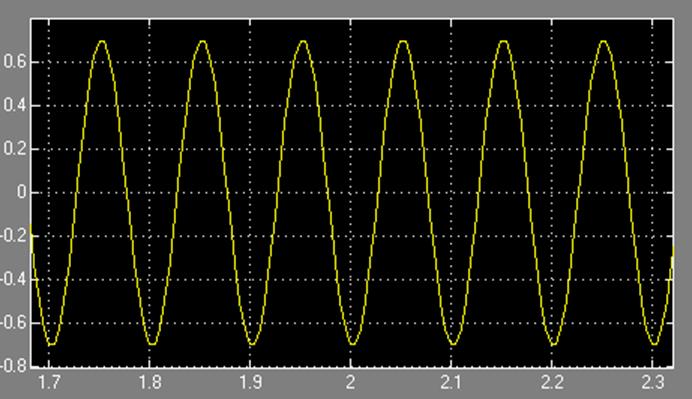
Рис. 18. Восстановленный сигнал, полученный с выхода блока TransferFcn.
Целью данного моделирования является наглядное представление процесса восстановления синусоидального сигнала (рис.16., рис.17., рис.18.). После прохождения сигнала через экстраполятор нулевого порядка видно, что он имеет «ступенчатую» форму не приемлемую для непрерывной синусоидальной волны. Именно за сглаживание сигнала и отвечает блок TransferFcn, рассчитанный с помощью фильтра Баттерворта 10 порядка. Он не пропускает гармоники с частотой среза выше, чем 10 Гц.
Задание №6:Заменить в отлаженной модели блок Zero-Order Hold на блок экстраполятора первого порядка First-Order Hold, скорректировать параметр Sample time, выполнить моделирование и пронаблюдать результаты:
Параметры исходного синусоидального сигнала: Частота 10 Гц, единичная амплитуда (A = 1).
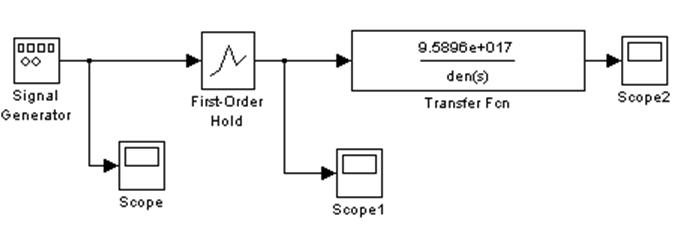
Рис. 19. Измененная модель дискретизации и восстановления синусоидального сигнала.
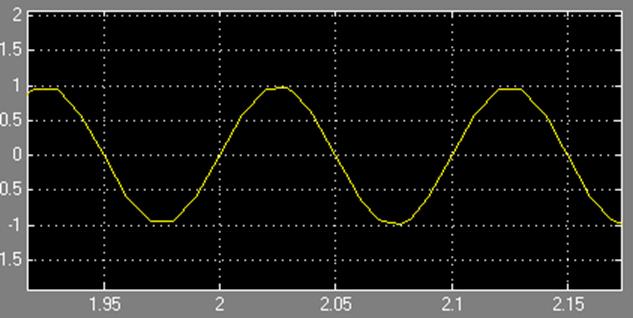
Рис. 20. Исходный дискретизируемый синусоидальный сигнал с частотой 10 Гц, полученный с выхода генератора сигналов.
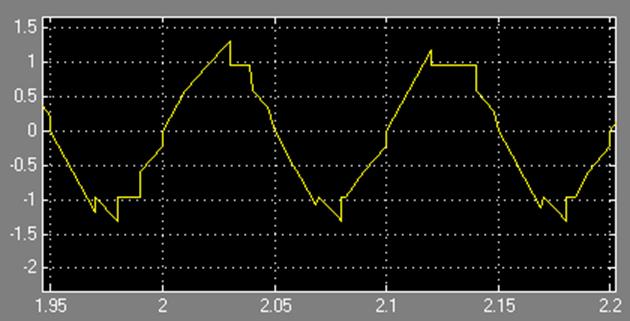
Рис. 21. Сигнал, полученный с выхода экстраполятора первого порядка, с тактом дискретности 0.01 сек.
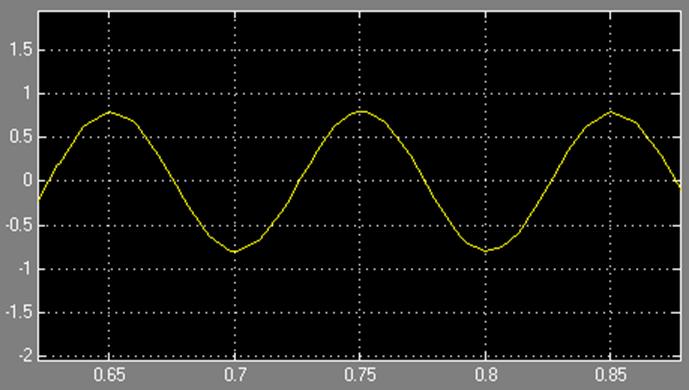
Рис. 22. Восстановленный сигнал, полученный с выхода блока TransferFcn.
В измененной модели (рис.19.) блок экстраполятора нулевого порядка заменен на блок экстраполятора первого порядка, поэтому на его выходе (рис.21.) сигнал представлен отсчетами, соединенными между собой прямыми линиями. Такт дискретности при этом увеличен с 0.005 до 0.01 сек., соответственно сглаживать такой сигнал значительно сложнее. Но блок TransferFcn, рассчитанный с определенным запасом (фильтр Баттерворта 10 порядка), позволяет получать сигнал на выходе, соответствующий исходной синусоидальной волне (рис.22.).
Выводы: В данной лабораторной работе мы рассмотрели различные модели дискретизации и восстановления сигналов. На практике подтверждена теорема Отсчётов. Восстановление непрерывного сигнала с помощью интерполяционного полинома вида: sin(x)/x дало наилучший результат. Использование интерполяционного полинома нулевого результата дало наихудший результат.
Все эти сведения, полученные на практике, дали нам более наглядное представление о том, как осуществляется преобразование аналоговых сигналов в цифровые последовательности и обратно в современных цифровых и вычислительных системах.
Литература:
1. Голышев Н.В., Щетинин Ю.И. Теория и обработка сигналов: Уч. пособие.- Новосибирск. Изд-во НГТУ, 1998 - ч.1.
2. Голышев Н.В., Щетинин Ю.И. Задачник-практикум по теории и обработке сигналов.: учеб. пособие. Новосибирск: Изд-во НГТУ, 2001
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.