Данный результат (рис.8.) наглядно иллюстрирует то, что при частоте гармонического сигнала равной частоте Найквиста мы можем восстановить исходный сигнал с некоторыми неточностями. Соответственно, частота отсчетов равная 2000Гц будет критической при восстановлении исходного сигнала.
При частоте отсчётов 4000 Гц получим:
% Программа генерации дискретного косинусоидального сигнала
f=1000; % Частота
Fd=2*f; T=1/Fd; % Частота и период отсчетов
t=0:T:60*T; y=cos(2*pi*f*t);
T1=1/4/f; t1=0:T1:60*T; y1=cos(2*pi*f*t1); % Период дискретизированного сигнала для частоты 4000Гц
plot(t,y,'-ok',t1,y1,'-.dr'); grid on
title('Sampling cosinusoidal signal')
xlabel('Time (sec)')
axis([0,40*T,-2,2])
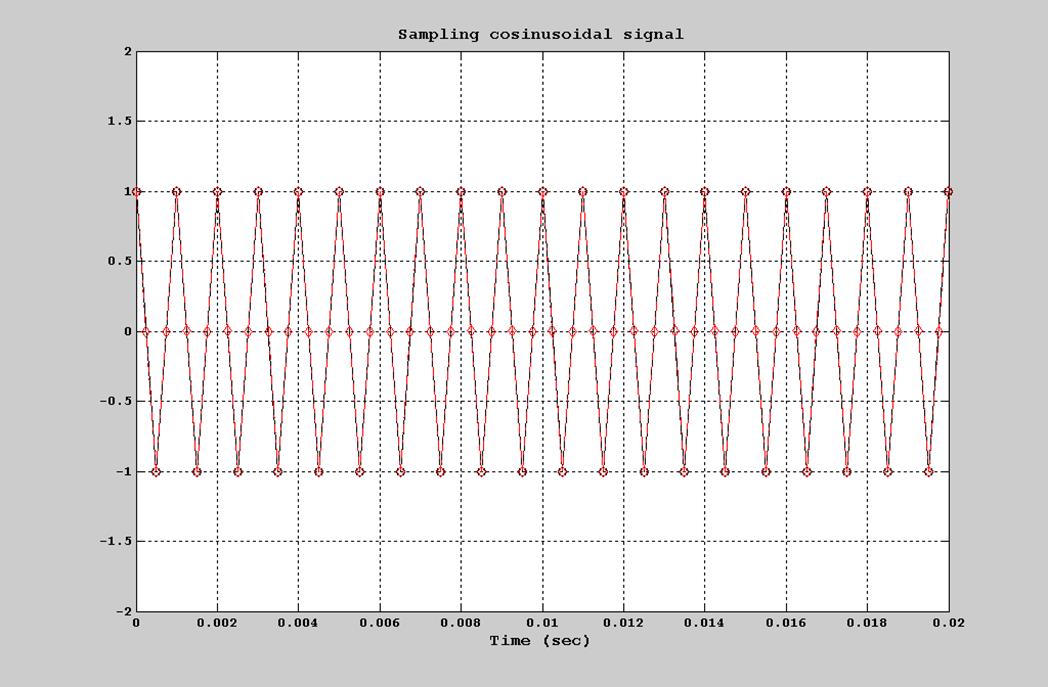
Рис. 9. График дискретного сигнала при частоте отсчётов 4000 Гц.
В данном случае (рис.9.) видно, что с ростом частоты отсчетов возрастает число точек, которые более подробно описывают исходный сигнал. Соответственно восстановление сигнала при большей частоте отсчетов является более точным и правильным.
При частоте 15000 Гц получим:
% Программа генерации дискретного косинусоидального сигнала
f=1000; % Частота
Fd=2*f; T=1/Fd; % Частота и период отсчетов
t=0:T:60*T; y=cos(2*pi*f*t);
T1=1/15/f; t1=0:T1:60*T; y1=cos(2*pi*f*t1); % Период дискретизированного сигнала для частоты 15000Гц
plot(t,y,'-ok',t1,y1,'-.dr'); grid on
title('Sampling cosinusoidal signal')
xlabel('Time (sec)')
axis([0,40*T,-2,2])
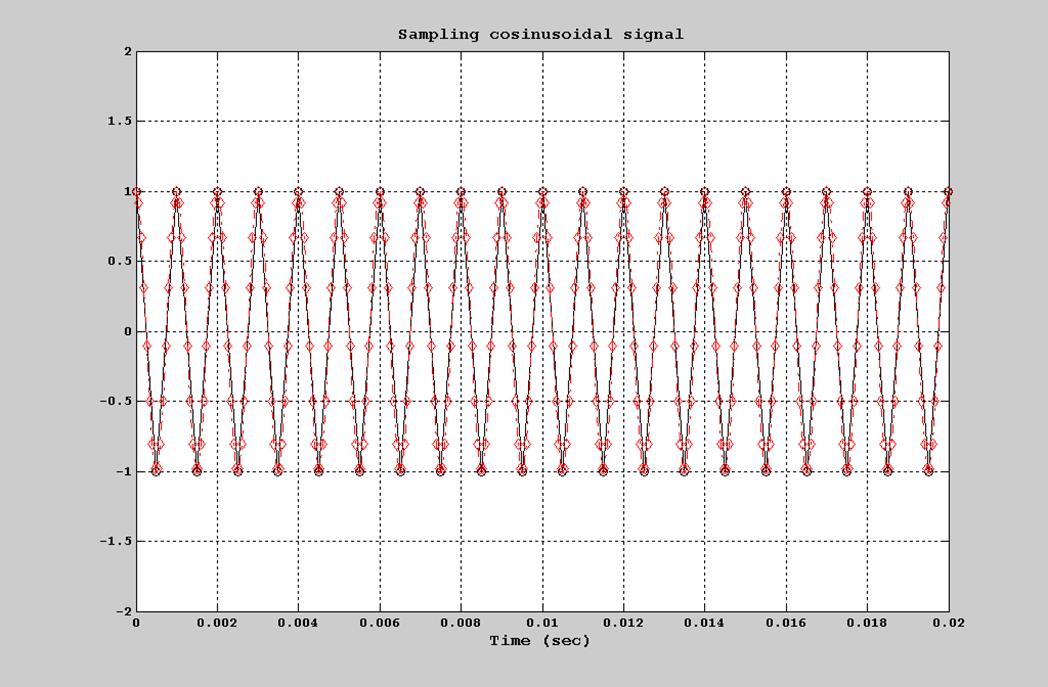
Рис. 10. График дискретного сигнала при частоте отсчётов 15000 Гц.
Вывод: Таким образом, при частоте отсчётов, меньшей частоты Найквиста, мы получаем неудовлетворительный результат. Так же чем выше частота, тем более точный восстановленный сигнал мы получаем.
Задание №4:Восстановление непрерывного сигнала по его отсчетам с использованием трех интерполяционных полиномов.
Файл-сценарий Matlab для генерирования восстановления сигнала с помощью идеального ФНЧ (Приложение 4 Процедура 4.1. методического указания):
% Программа демонстрации восстановления сигнала
% интерполяционным полиномом sin(x)/x
% вариант интерполяции с помощью идеального ФНЧ
t=-3:0.01:7; % задание интервала времени
n=-3:7; % номера отсчетов сигнала
s=[0 0 2.5 6.4 3 4.2 1 -2.5 0 -1 0]; % дискретный сигнал
d=[n' s']; % параметры для функции pulstran
y=pulstran(t,d,'sinc'); % восстановленный сигнал
plot(n, s, 'o', t, y); grid on % график восстановленного сигнала
hold on
% построение графиков отдельных sinc импульсов
for k=1:length(s),plot(t,s(k)*sinc(t-n(k)), ':'), end
hold off
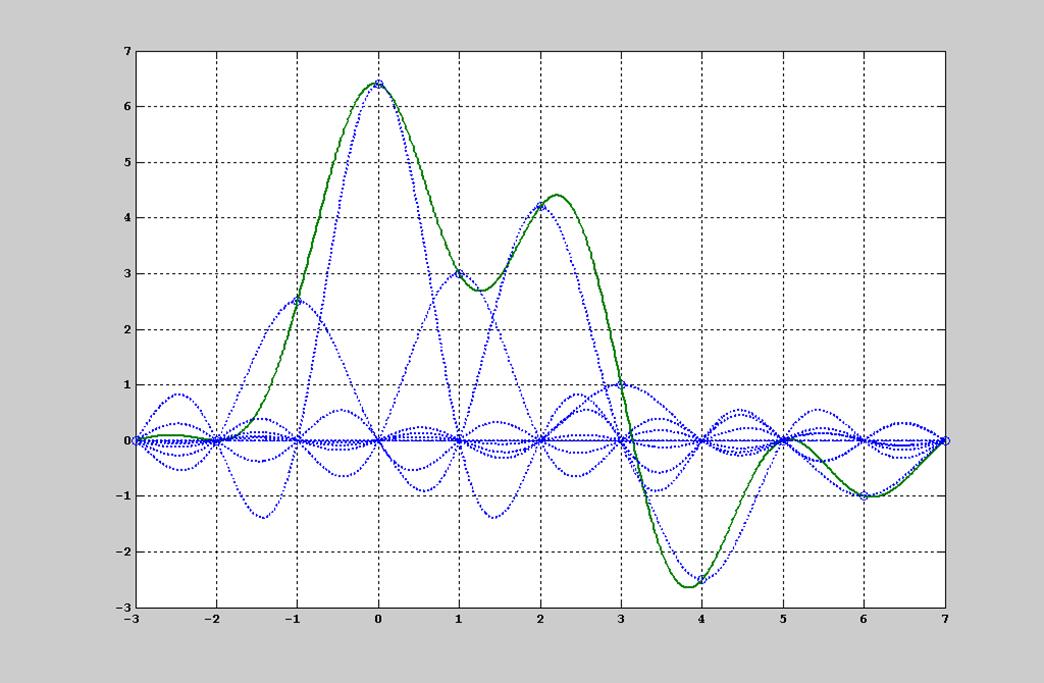
Рис. 11. График восстановления сигнала интерполяционным полиномом sin(x)/x (вариант интерполяции с помощью идеального ФНЧ).
Интерполяция – повышение частоты дискретизации в целое число раз с заполнением промежутков между отсчетами.
Данный способ
восстановления сигнала основывается на теореме Отсчётов (если сигнал не имеет спектральных составляющих с f
> fmax, то он полностью определяется своими отсчетами в
дискретные моменты времени через интервал отсчетов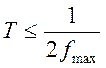 
). Используя набор дискретных отсчетов сигнала 
и базис Котельникова 
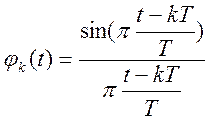, мы можем сформировать непрерывный
сигнал (рис. 11.) [1]. Функция pulstran очень
удобна в процессе восстановления, так как она позволяет строить сигнал в виде
суммы конечного числа импульсов произвольной формы с заданными задержками и
множителями.
Восстановление аналогового сигнала с помощью интерполяционных полиномов нулевого и первого порядков
Ряд Тейлора в точках 
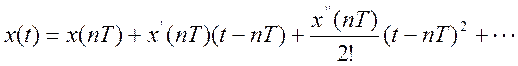
Нулевой порядок : 
Первый порядок: 
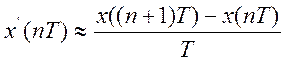- метод экстраполяции
«вперед»
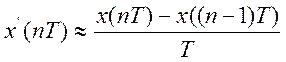- метод экстраполяции
«назад»
Файл-сценарий Matlab для генерирования восстановления сигнала с помощью интерполяционного полинома нулевого порядка (Приложение 4 Процедура 4.2. методического указания):
% Программа демонстрации восстановления сигнала
% с помощью интерполяционного полинома нулевого порядка
t=-3:0.01:7; % задание интервала времени
n=-3:7; % номера отсчетов сигнала
s=[0 0 2.5 6.4 3 4.2 1 -2.5 0 -1 0]; % дискретный сигнал
d=[n' s']; % параметры для функции pulstran
% сигнал,восстановленный полиномом нулевого порядка
y=pulstran(t,d,'rectpuls');
plot(n, s,'o', t, y) % график восстановленного сигнала
hold on
% сигнал,восстановленный интерполятором sinc
y1=pulstran(t,d,'sinc');
plot(t, y1,'-.m'); grid on
% построение графиков отдельных прямоугольных импульсов
for k=1:length(s),plot(t,s(k)*rectpuls(t-n(k)), ':'), end
hold off
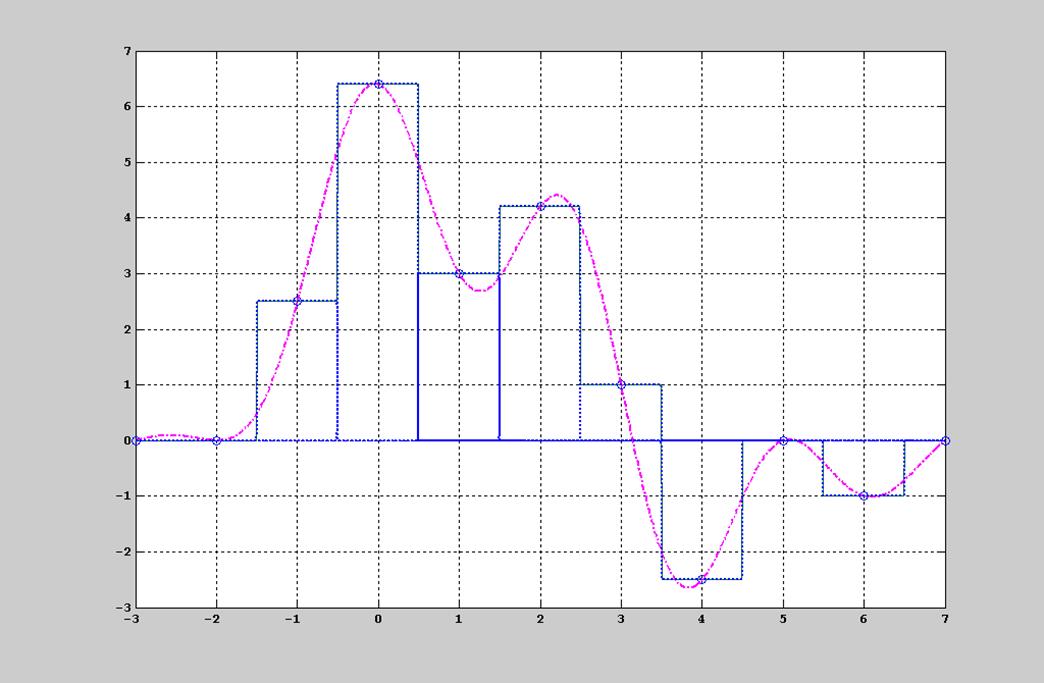
Рис. 12. График восстановления сигнала с помощью интерполяционного полинома нулевого порядка.
В данной программе восстановление сигнала производится с
помощью интерполяции полиномом нулевого порядка, и заполнение промежутков между
отсчетами осуществляется с помощью прямоугольных импульсов. Данный способ
восстановления сигнала является простейшей ступенчатой аппроксимацией (). По этому принципу построены
фиксаторы (экстраполяторы) нулевого порядка. При достаточно большом числе
отсчетов экстраполяторы нулевого порядка генерируют непрерывный сигнал, близкий
к исходному.
На графике мы видим ступени. Малое количество ступеней грубо экстраполирует исходный сигнал. Требуется увеличить частоту отсчётов.
Файл-сценарий Matlab для генерирования восстановления сигнала с помощью интерполяционного полинома первого порядка (Приложение 4 Процедура 4.3. методического указания):
% Программа демонстрации восстановления сигнала
% с помощью интерполяционного полинома первого порядка
t=-3:0.01:7; % задание интервала времени
n=-3:7; % номера отсчетов сигнала
s=[0 0 2.5 6.4 3 4.2 1 -2.5 0 -1 0]; % дискретный сигнал
d=[n' s']; % параметры для функции pulstran
tau=2;% длительность треугольного сигнала
% сигнал,восстановленный полиномом первого порядка
y=pulstran(t,d,'tripuls',tau);
plot(n, s,'o', t, y) % график восстановленного сигнала
hold on
%сигнал,восстановленный интерполятором sinc
y1=pulstran(t,d,'sinc');
plot(t, y1,'-.m'),grid on
% построение графиков отдельных треугольных импульсов
for k=1:length(s),plot(t,s(k)*tripuls(t-n(k),tau), ':'), end
hold off
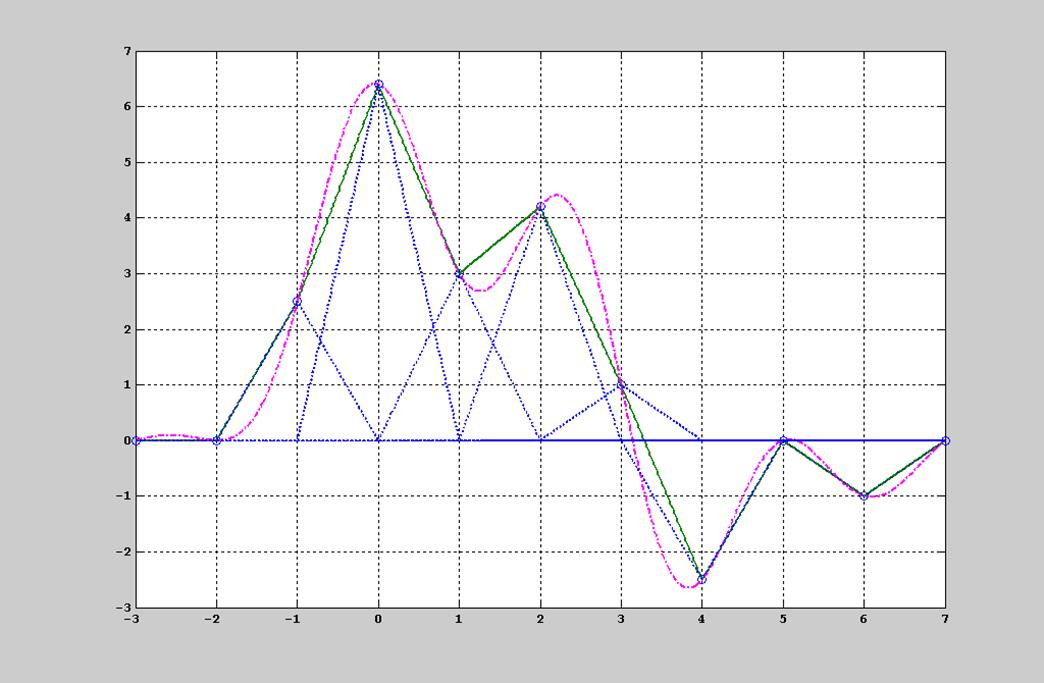
Рис. 13. График восстановления сигнала с помощью интерполяционного полинома первого порядка.
Как видно из рис. 13., при небольшом числе отсчетов восстановление
интерполяционным полиномом первого порядка не дает такого наглядного
представления сигнала, как восстановление по интерполяционному полиному
sin(x)/x. Экстраполяторы первого порядка, построенные на принципе 
, когда отдельные отсчеты дискретного
сигнала соединяются прямыми линиями, дают неплохой результат для большого числа
отсчетов (размеры прямых соединительных линий уменьшаются, тем самым более
точно воспроизводя форму исходного сигнала). Очень часто экстраполирование первого
порядка применяется в вычислительных программных пакетах, где графики функций
строятся с помощью соединения точек прямыми линиями.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.