Изучение сущности и моделей дискретизации (квантования по времени) сигналов и методов восстановления непрерывных сигналов по отсчетам, страница 3

С помощью следующего script-файла проведём восстановление сигнала по отсчётам с помощью интерполяционного полинома нулевого порядка.

t=-3:0.01:7; % задание интервала времени

n=-3:7;   % номера отсчетов сигнала

s=[0  0  2.5  6.4  3  4.2  1  -2.5  0  -1  0]; % дискретный сигнал

d=[n' s'];  % параметры для функции pulstran

% сигнал,восстановленный полиномом нулевого порядка

y=pulstran(t,d,'rectpuls');

plot(n, s,'o', t, y)  % графики  сигналов

hold on

% сигнал,восстановленный интерполятором sinc

y1=pulstran(t,d,'sinc');

plot(t, y1,'-.m')

% построение графиков отдельных прямоугольных импульсов

for k=1:length(s),plot(t,s(k)*rectpuls(t-n(k)), ':'), end

Полученные результаты представлены на рис. 11.

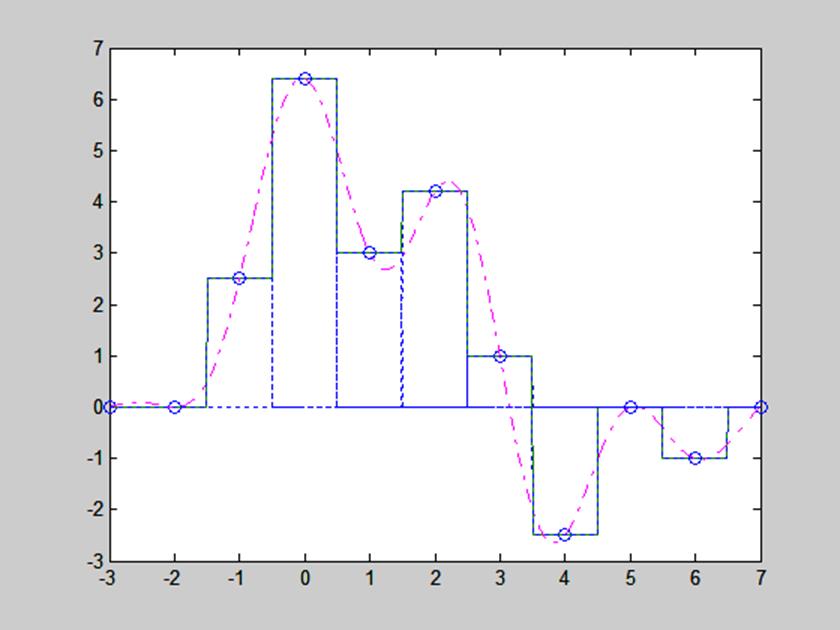
Рис. 11. Сигнал, восстановленный с помощью полинома нулевого порядка.

На рис. 11 видим, что сигнал восстанавливается неточно, присутствуют ступеньки.

Преимуществом способа является его простота, т.к. для восстановления сигнала требуются только значения сигнала в точках отсчёта.

7.3.  Восстановление сигнала с помощью полинома первого порядка.

Кроме полинома нулевого порядка для восстановления аналогового сигнала по его отсчетам используются также полиномы первого порядка, в которых кроме отсчета сигнала  необходима также его первая производная.

С помощью следующего script-файла проведём восстановление сигнала по отсчётам с помощью интерполяционного полинома первого порядка.

t=-3:0.01:7; % задание интервала времени

n=-3:7;   % номера отсчетов сигнала

% дискретный сигнал

s=[0  0  2.5  6.4  3  4.2  1  -2.5  0  -1  0];

d=[n' s']; % параметры для функции pulstran

tau=2;  % длительность треугольного сигнала

% сигнал,восстановленный полиномом первого порядка

y=pulstran(t,d,'tripuls',tau);

plot(n, s,'o', t, y) % график восстановленного сигнала

hold on

%сигнал,восстановленный интерполятором sinc

y1=pulstran(t,d,'sinc');

plot(t, y1,'-.m')

hold off

Полученные результаты представлены на рис. 12.

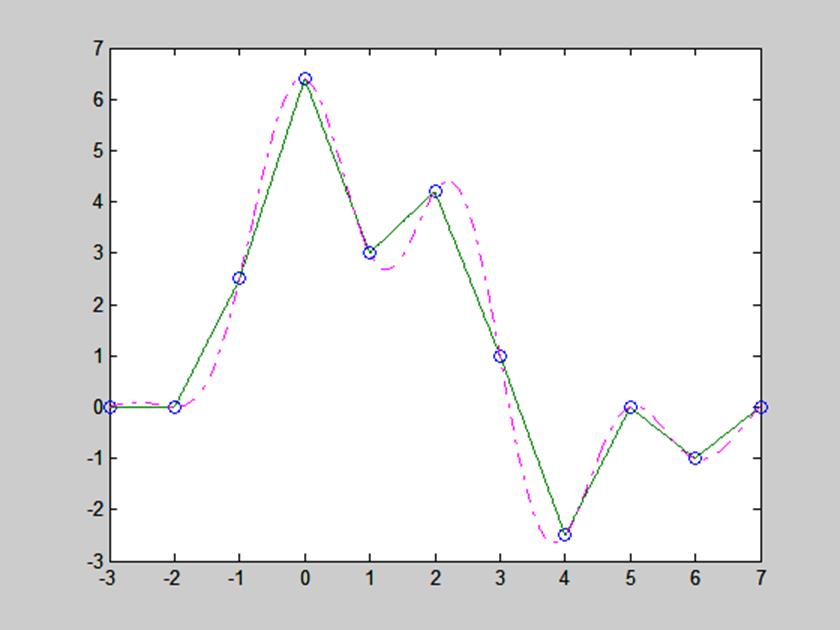
Рис. 12. Сигнал, восстановленный с помощью полинома первого порядка.

На рис. 12 видим, что при восстановлении с помощью полинома первого порядка соседние отсчеты соединяются прямыми линиями.

Сравнив рис. 11 и 12, видим, что восстановление с помощью полинома первого порядка производится точнее, чем с помощью полинома нулевого порядка при одинаковом числе отсчётов, но второй способ более сложный, так как в каждой точке необходимо вычисление первой производной сигнала.

7.4.  Восстановление сигнала с помощью полинома нулевого порядка и ФНЧ.

 Ступеньки, получаемые при восстановлении сигнала с помощью полинома нулевого порядка можно устранить с помощью выходного ФНЧ.

С помощью следующего script-файла проведём восстановление сигнала по отсчётам с помощью интерполяционного полинома нулевого порядка и произведём сглаживание восстановленного с помощью ФНЧ.

% Программа демонстрации восстановления сигнала

% с помощью интерполяционного полинома нулевого порядка и ФНЧ,

% используемого для сглаживания восстановленного сигнала

t=-3:0.01:7; % задание интервала времени

n=-3:7;   % номера отсчетов сигнала

s=[0  0  2.5  6.4  3  4.2  1  -2.5  0  -1  0]; % дискретный сигнал

d=[n' s']; % параметры для функции pulstran

% сигнал,восстановленный полиномом нулевого порядка

y=pulstran(t,d,'rectpuls');

% фильтрация восстановленного сигнала

[b,a]=butter(6,2*pi*0.5,'s'); % получение характеристик фильтра
% Баттерворта

lsim(b,a,y,t); %  фильтрация и построение графика после фильтрации

hold on; axis([-3,8,-4,8])

plot(n, s,'o', t, y) % график восстановленного сигнала

hold on

% сигнал,восстановленный интерполятором sinc

y1=pulstran(t,d,'sinc');

plot(t, y1,'-.m')

% построение графиков отдельных прямоугольных импульсов

for k=1:length(s),plot(t,s(k)*rectpuls(t-n(k)), ':'), end

hold off

Полученные результаты представлены на рис. 13.

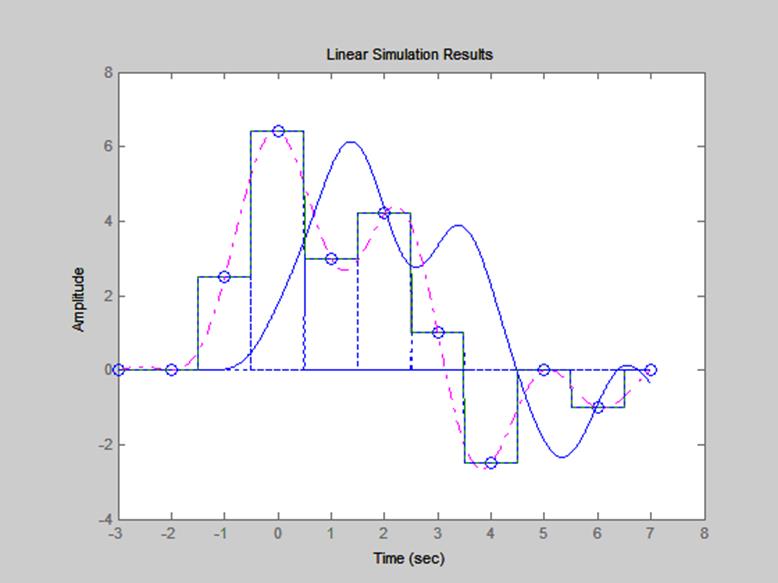
Рис.13.   Сигнал, восстановленный с помощью полинома

нулевого порядка и ФНЧ.

На рис. 13 видим, что после фильтрации восстановленного сигнала с помощью ФНЧ произошло сглаживание ступенек и, вместе с этим, появляется временной сдвиг сигнала.

Итак, были рассмотрены три способа восстановления сигнала по его отсчётам.

Наиболее точные результаты дало восстановление сигнала с помощью ряда Котельникова. Однако, оно неосуществимо на практике, т.к. невозможно обеспечить идеальный ФНЧ и бесконечное число членов ряда. Поэтому для решения задач восстановления сигналов часто используют полиномы нулевого и первого порядка, которые обладают меньшей точностью, но проще в использовании.

Хорошие результаты даёт фильтрация восстановленных с помощью полиномов нулевого и первого порядка сигналов.

Выводы:

1.  Теорема отсчётов является основной теоремой дискретизации сигналов и утверждает, что если сигнал не имеет спектральных составляющих с частотами выше f_m, то он полностью определяется своими отсчетами в дискретные моменты времени через интервал отсчетов 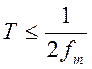  или с частотой  отсчетов . 

2. Если частота отсчетов  , то происходит наложение спектров дискретного сигнала и его невозможно точно восстановить по отсчётам.

 В п. 3 и 4 было показано, что при дискретизации гармонических сигналов с частотой отсчётов  возникает наложение, частот. При этом гармоники сворачиваются относительно частоты Найквиста 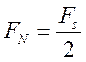. Например, гармоника 6000 Гц при дискретизации с частотой 8192 Гц подменяется гармоникой частотой около 2200 Гц (рис. 5) и при той же частоте отсчётов сигналы 6000 и 5000 Гц звучат ниже, чем 4000 Гц.

3. В п.7 были рассмотрены три способа восстановления сигнала по его отсчётам.

Наиболее точные результаты дало восстановление сигнала с помощью ряда Котельникова (рис. 10). Однако, оно неосуществимо на практике, т.к. невозможно обеспечить идеальный ФНЧ и бесконечное число членов ряда. Поэтому для решения задач восстановления сигналов обычно используют полиномы нулевого (рис. 11) и первого (рис. 12) порядка, которые обладают меньшей точностью, но проще в использовании.

Хорошие результаты даёт фильтрация восстановленных с помощью полиномов нулевого и первого порядка сигналов (рис. 13).