X=fft(x,length(f));
X1=fftshift(X);
subplot(211), plot(t(1:50),x(1:50),'-o')
set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)
legend('Сигнал'), xlabel('Время, с')
subplot(212), plot(f,abs(X1)*1/fs)
set(gca, 'FontName','Times New Roman Cyr', 'FontSize', 10)
legend('Амплитудный спектр'), xlabel('Частота, Гц')
Полученные результаты представлены на рис.6 и рис.7.
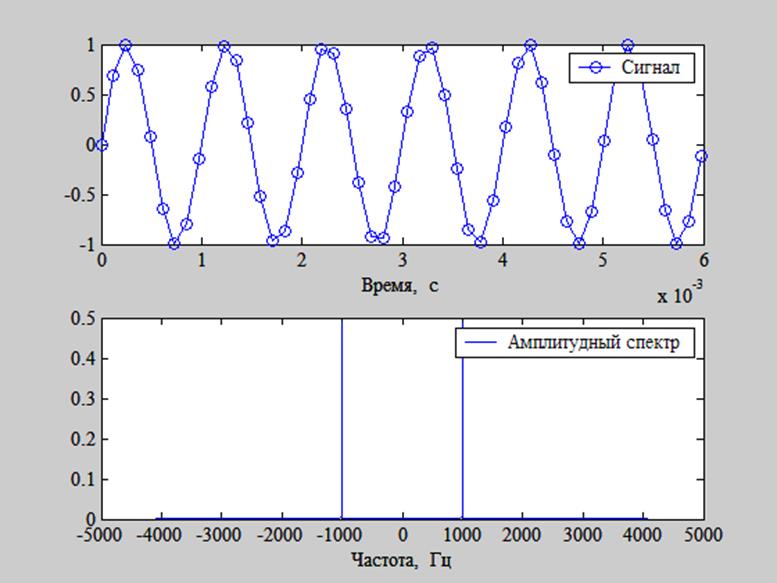
Рис. 6. График амплитудного спектра гармоники частотой 1000 Гц
при Fs= 8192 Гц.
На рис. 6 видим, что амплитудный спектр гармоники частотой 1000 Гц совпадает с теоретическими ожиданиями: присутствует только частота 1000 Гц, т.е. в данном случае наложения спектров не происходит.
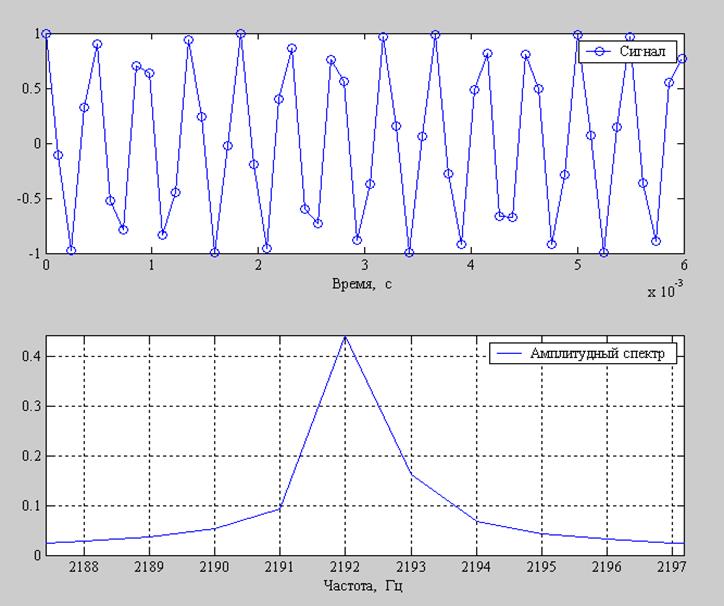
Рис. 7. График амплитудного спектра гармоники частотой 6000 Гц
при Fs= 8192 Гц.
На рис.7 видим, что произошла подмена гармоники частотой 6000 Гц на гармонику 2192 Гц, что является результатом наложения спектров и является причиной совпадения звучания этих сигналов, о котором говорилось в п. 3.
5. Изучение частотно-временного характера сигнала с линейно меняющейся частотой.
С помощью следующей последовательности команд сгенерируем сигнал с линейно изменяющейся частотой длительностью 10 с, частотой отсчетов 8192 Гц, начальным значением частоты 1000 Гц, значением частоты 4000 Гц через 3 с. и прослушаем звучание данного сигнала.
Fs = 8192;
t = 0: 1/Fs: 10;
x = chirp(t, 1000, 3, 4000);
sound(x)
Прослушав звучание сгенерированного сигнала, определили, что тон сигнала повышается до момента времени 3 сек., далее понижается и в момент времени около 7 сек. снова начинается повышение.
Вычислим моменты времени, в которые тон звука начинает понижаться и повышаться аналитически.
Частота
сигнала изменяется по линейному закону ![]() .
.
Частота
отсчётов Fs = 8192 Гц, следовательно, частота Найквиста 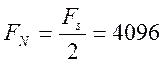 Гц и начиная с неё будет наблюдаться
сворачивание гармоник относительно
Гц и начиная с неё будет наблюдаться
сворачивание гармоник относительно ![]() .
.
Таким
образом, частота должна повышаться от 1000 Гц до ![]() ,
понижаться до момента достижения
,
понижаться до момента достижения ![]() и далее
повышаться.
и далее
повышаться.
Исходя
из линейного закона изменения частоты, получаем, что сигнал достигает частоты ![]() Гц в момент времени, равный
приблизительно 3 сек., и частоты
Гц в момент времени, равный
приблизительно 3 сек., и частоты ![]() Гц в момент 7.2
сек. Получили данные, совпадающие с экспериментальными.
Гц в момент 7.2
сек. Получили данные, совпадающие с экспериментальными.
Используя процедуру specgram(x,[],Fs)построим спектрограмму сгенерированного выше сигнала.
Полученные результаты представлены на рис.8.
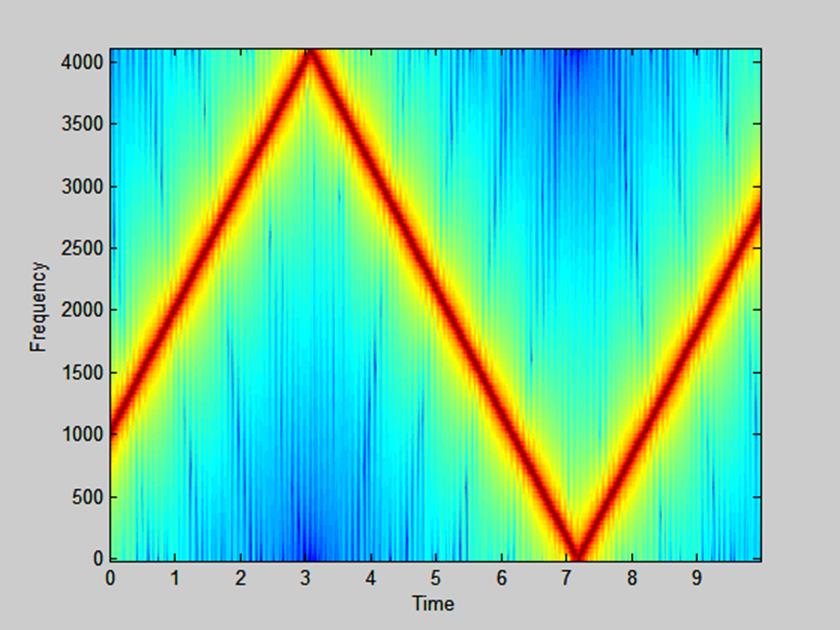
Рис. 8. Спектрограмма сигнала с линейно меняющейся частотой.
На рис. 8 видим, что частота сигнала не изменяется по линейному закону.
Это
является результатом сворачивания гармоник относительно частоты Найквиста
(частоты сворачивания) ![]() , которая
является максимальной частотой сигнала, который можно определить с помощью отсчётов,
взятых с частотой
, которая
является максимальной частотой сигнала, который можно определить с помощью отсчётов,
взятых с частотой ![]() .
.
6. Восстановление сигнала полиномом нулевого порядка.
Сигнал может быть восстановлен полиномом нулевого порядка по выражению
![]()
![]()
Т.е. свёртка импульсной характеристики полинома нулевого порядка и значений сигнала в точках отсчёта даёт восстановленный сигнал.
Функция interp0() формирует импульсную характеристику полинома нулевого порядка.
function u=interp0(t,T,n)
% Функция для формирования
% ИХ полинома нулевого порядка
% синтаксис interp0(t,T,n)
% t - время, T-интервал отсчетов,
% n - номер отсчета
u=(t>=(n-1)*T)-(t>=n*T);
С помощью следующего script-файла проведём восстановление сигнала по его отсчётам с помощью полинома нулевого порядка.
% программа восстановления
% сигнала полиномом нулевого порядка
f=10; % частота сигнала
Fs=f*20; % частота отсчетов
T=1/Fs; % интервал отсчетов
t=0:T:1/f; % шкала дискретного времени
x=cos(2*pi*f*t); % сигнал
t1=0:0.0001:1/f; % "непрерывное" время
N=Fs/f; % число отсчетов сигнала
y=zeros(1, length(t1));
% вычисление сверток сигнала
% и ИХ экстраполятора в цикле
for k=1:(N+1), y1=conv(x(k), interp0(t1,T,k));, y=y+y1; end
subplot(211), plot(t1,y)
hold on
x1=cos(2*pi*f*t1);
plot(t1,x1,'-.r')
hold off
% построение отдельной свертки
subplot(212), plot(t1,conv(x(3), interp0(t1,T,3)))
xlabel('Time, sec')
Полученные результаты представлены на рис.9.
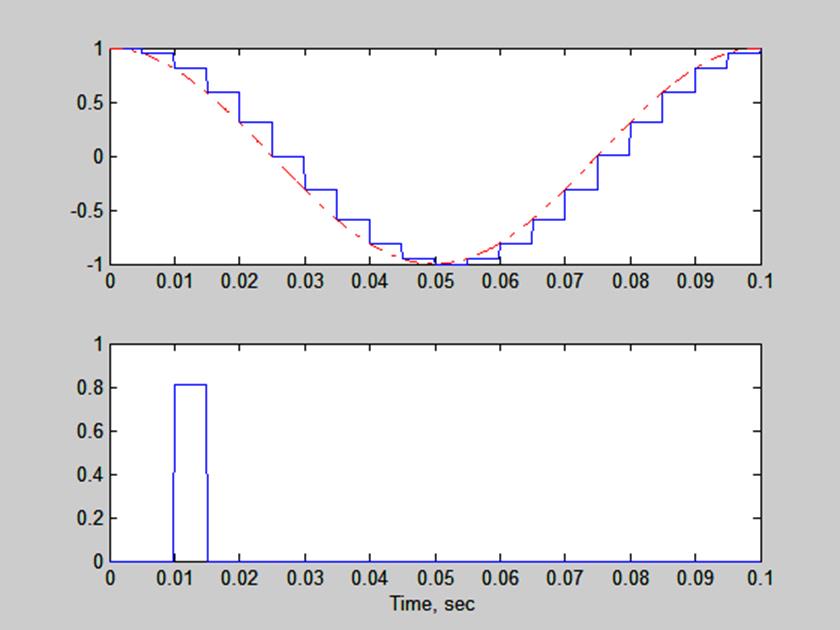
Рис. 9. Сигнал, восстановленный полиномом нулевого порядка.
На рис. 9 видим, что сигнал восстанавливается неточно. Восстановленный сигнал имеет ступенчатый вид, значения сигнала остаются постоянными до получения последующего отсчёта.
7. Моделирование восстановления непрерывного сигнала по его отсчетам с использованием различных интерполяционных полиномов.
7.1. Восстановление сигнала с помощью идеального ФНЧ.
Во
временной области сигнал может быть точно восстановлен по его отсчетам с
помощью интерполяционного полинома Котельникова (выражение (1)).
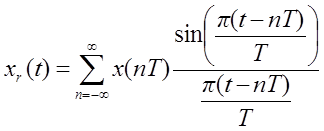 (1)
(1)
С помощью следующего script-файла проведём восстановление сигнала по отсчётам с помощью идеального ФНЧ.
% Программа демонстрации восстановления сигнала
% интерполяционным полиномом sin(x)/x
% вариант интерполяции с помощью идеального ФНЧ
t=-3:0.01:7; % задание интервала времени
n=-3:7; % номера отсчетов сигнала
s=[0 0 2.5 6.4 3 4.2 1 -2.5 0 -1 0];% дискретный сигнал
d=[n' s']; % параметры для функции pulstran
y=pulstran(t,d,'sinc');
% график дискретного сигнала
plot(n, s,'o',t,y)
hold on
% построение графиков отдельных sinc импульсов
for k=1:length(s), plot(t, s(k)*sinc(t-n(k)), ':'), end
grid
hold off
Полученные результаты представлены на рис. 10.
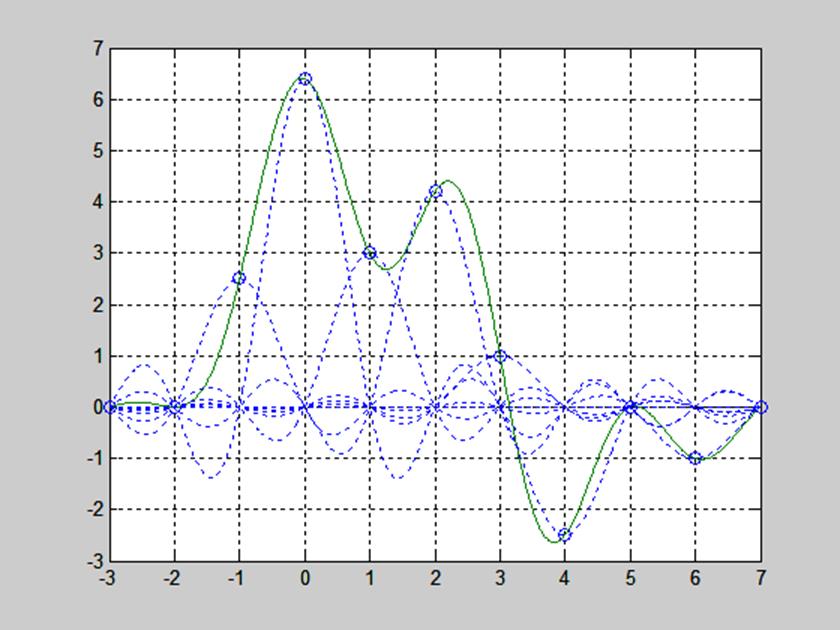
Рис. 10. Иллюстрация восстановления сигнала с помощью идеального ФНЧ.
На рис. 10 видим, что ряд точно представляет исходный сигнал в точках отсчёта и сходится к нему во всех остальных точках.
Точное восстановление сигнала с помощью интерполяционного ряда Котельникова требует идеального ФНЧ и бесконечного числа членов ряда, что на практике невозможно обеспечить, поэтому для восстановления чаще применяются другие способы.
7.2. Восстановление сигнала с помощью полинома нулевого порядка.
На практике для восстановления непрерывного сигнала по его отсчетам широко используют восстановление с помощью полиномов нулевого порядка, при котором используются только значения x(nT). Этот способ восстановления сигнала является наиболее простым.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.