








Лекция 4
4. СФЕРИЧЕСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА.
Сферическим называется движение твердого тела имеющего одну неподвижную точку.
Тело D совершает сферическое движение относительно неподвижной точки О (рис. 4.1). Точки тела D движутся по сферам с центром в точке О.
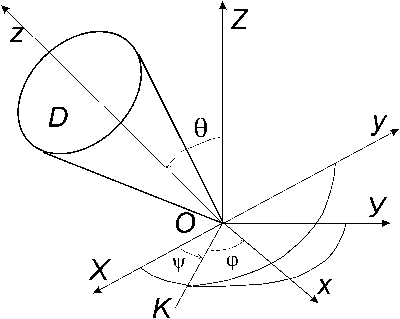
Рис. 4.1
Для
характеристики сферического движения тела введем две ортогональные системы
отсчета c началом координат в неподвижной точке О:
неподвижную ОХУZ и подвижную Охуz, связанную с телом D и
движущуюся вместе с ним относительно точки О. Прямая ОК,
являющаяся линией пересечения плоскости ХУ с плоскостью ху,
называется линией узлов. Положение подвижной системы Охуz относительно неподвижной
ОХУZ можно задать с помощью углов Эйлера:
угла прецессии ![]() ,
угла собственного вращения
,
угла собственного вращения ![]() и угла нутации
и угла нутации ![]() . Следовательно, для задания
сферического движения твердого тела необходимо задать углы Эйлера как функции
времени:
. Следовательно, для задания
сферического движения твердого тела необходимо задать углы Эйлера как функции
времени:
![]() . (4.1)
. (4.1)
Уравнения
(4.1) называются уравнениями сферического движения твердого тела. При
изменении только угла ![]() тело
D будет вращаться вокруг оси ОZ с угловой скоростью
тело
D будет вращаться вокруг оси ОZ с угловой скоростью ![]() ; при изменении только угла
; при изменении только угла ![]() тело D
будет вращаться вокруг оси Оz с угловой
скоростью
тело D
будет вращаться вокруг оси Оz с угловой
скоростью ![]() ; при изменении
только угла
; при изменении
только угла ![]() тело D будет вращаться вокруг линии узлов ОК с угловой скоростью
тело D будет вращаться вокруг линии узлов ОК с угловой скоростью ![]() (рис. 4.2). При движении тела D все три угла Эйлера меняются одновременно, и
результирующее движение будет вращательным движением с мгновенной угловой
скоростью
(рис. 4.2). При движении тела D все три угла Эйлера меняются одновременно, и
результирующее движение будет вращательным движением с мгновенной угловой
скоростью
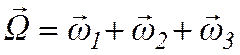 . (4.2)
. (4.2)
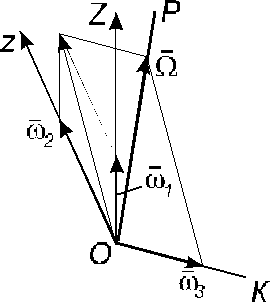
Прямая ОР
вдоль которой направлен вектор мгновенной угловой скорости ![]() результирующего вращения называется мгновенной
осью вращения тела. При сферическом движении тела D
мгновенная ось ОР меняет свое положение в пространстве, при этом вектор
мгновенной угловой скорости
результирующего вращения называется мгновенной
осью вращения тела. При сферическом движении тела D
мгновенная ось ОР меняет свое положение в пространстве, при этом вектор
мгновенной угловой скорости ![]() изменяется
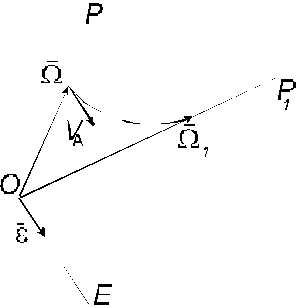
как по величине, так и по направлению (рис. 4.3). Угловым ускорением тела в
момент времени t называется вектор
изменяется
как по величине, так и по направлению (рис. 4.3). Угловым ускорением тела в
момент времени t называется вектор
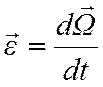 . (4.3)
. (4.3)
С другой стороны согласно (1.2)
скорость точки А – конца вектора мгновенной угловой скорости ![]()
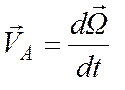 .
.
Следовательно, при
сферическом движении тела вектор углового ускорения ![]() в каждый момент времени направляется
как скорости
в каждый момент времени направляется
как скорости ![]() конца
вектора мгновенной угловой скорости
конца
вектора мгновенной угловой скорости ![]() тела и прикладывается в неподвижной
точке О (рис. 4.3):
тела и прикладывается в неподвижной
точке О (рис. 4.3):
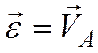 .
(4.4)
.
(4.4)
Прямая ОЕ, вдоль которой
направлен вектор углового ускорения ![]() , называется осью
углового ускорения.
, называется осью
углового ускорения.
При
сферическом движении тела направления векторов ![]() и
и ![]() не совпадают.
не совпадают.
Для
определения скорости произвольной точки М тела D
проведем из неподвижной точки О в точку М радиус вектор ![]() . Тогда согласно (1.2) и (2.18)
. Тогда согласно (1.2) и (2.18)
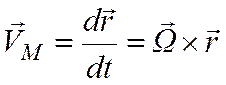 , (4.5)
, (4.5)
поскольку вектор ![]() постоянный по модулю, т.к.
расстояние между точками О и М абсолютно твердого тела при
движении не изменяется. Следовательно, при сферическом движении тела
скорость любой его точки определяется как её вращательная скорость вокруг
мгновенной оси.
постоянный по модулю, т.к.
расстояние между точками О и М абсолютно твердого тела при
движении не изменяется. Следовательно, при сферическом движении тела
скорость любой его точки определяется как её вращательная скорость вокруг
мгновенной оси.
Для определения величины скорости точки М опустим из этой точки на мгновенную ось ОР перпендикуляр hp. Тогда
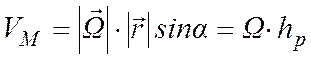 . (4.6)
. (4.6)
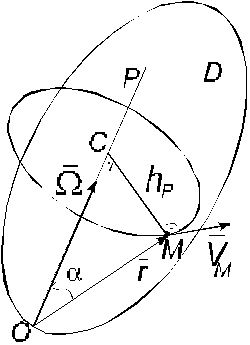
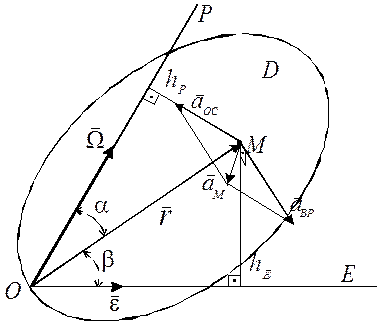
Вектор 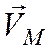 направлен согласно (4.5)
перпендикулярно плоскости, проходящей через точку М и мгновенную ось
вращения ОР в направлении
направлен согласно (4.5)
перпендикулярно плоскости, проходящей через точку М и мгновенную ось
вращения ОР в направлении ![]() (
(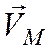
![]() hp,рис. 4.4).
hp,рис. 4.4).
Для определения ускорения точки М тела при сферическом движении вычислим производную по времени от равенства (4.5):
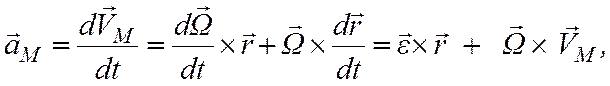
или
![]() . (4.7)
. (4.7)
Здесь
![]() (4.8)
(4.8)
называется вращательным ускорением точки М, а
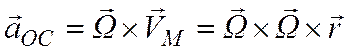 (4.9)
(4.9)
-осестремительным ускорением точки М.
Следовательно, ускорение любой точки при сферическом движении определяется как геометрическая сумма её вращательного и осестремительного ускорений.
Модули осестремительного и вращательного ускорений определяются по формулам:
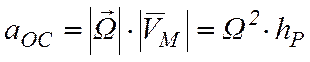 , (4.10)
, (4.10)
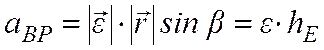 , (4.11)
, (4.11)
где ![]() - величина перпендикуляра опущенного из точки
М на ось углового ускорения ОЕ. Вектор осестремительного
ускорения
- величина перпендикуляра опущенного из точки
М на ось углового ускорения ОЕ. Вектор осестремительного
ускорения ![]() направлен согласно (4.9) из точки М
к мгновенной оси ОР (вдоль hp,
рис. 4.5). Вектор вращательного ускорения
направлен согласно (4.9) из точки М
к мгновенной оси ОР (вдоль hp,
рис. 4.5). Вектор вращательного ускорения ![]() согласно
(4.8) направлен в точке М перпендикулярно плоскости, походящей через эту
точку и ось углового ускорения ОЕ в направлении
согласно
(4.8) направлен в точке М перпендикулярно плоскости, походящей через эту
точку и ось углового ускорения ОЕ в направлении ![]() (рис.
4.5).
(рис.
4.5).
Вектор
полного ускорения точки ![]() при
сферическом движении определяется диагональю параллелограмма построенного на
векторах
при
сферическом движении определяется диагональю параллелограмма построенного на
векторах ![]() и
и ![]() как на сторонах (рис. 4.5). Поэтому
модуль
как на сторонах (рис. 4.5). Поэтому
модуль ![]() определяется по
формуле
определяется по
формуле
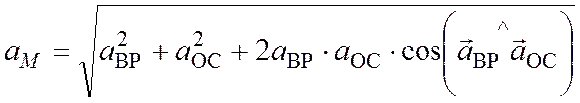 . (4.12)
. (4.12)
ДВИЖЕНИЕ СВОБОДНОГО ТВЕРДОГО ТЕЛА
Рассмотрим свободное твердое тело D, движущееся относительно неподвижной системы отсчета Охуz (рис. 4.6). Положение тела в любой момент времени однозначно определяется заданием произвольного жестко связанного с ним треугольника М1М2М3, т.е. заданием девяти декартовых координат, определяющих положения вершин этого треугольника.
Однако так как расстояния между вершинами треугольника при его движении не изменяются (как расстояния между любыми точками твердого тела), то координаты вершин будут связаны друг с другом соотношениями:
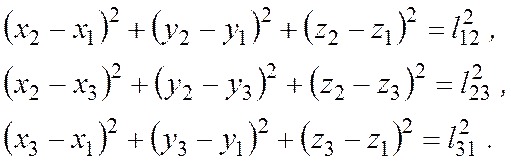
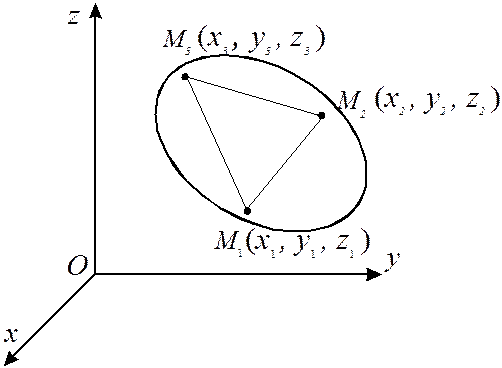
Рис. 4.6
Здесь xk, yk, zk (k= 1, 2, 3) - декартовые координаты k - ой вершины треугольника М1М2М3, l12, l23, l31 - расстояния между соответствующими вершинами этого треугольника. Поэтому, для определения положения тела Dдостаточно задать шесть декартовых координат, остальные три могут быть найдены с помощью выше записанных уравнений.
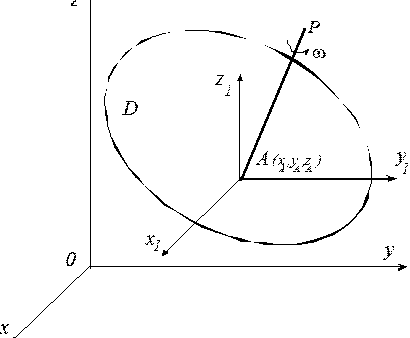
Рис. 4.7
Число S независимых координат, однозначно определяющих положение тела в пространстве равно числу степеней свободы тела. Следовательно, для свободного твердого тела S = 6.
Обычно
в качестве независимых координат выбирают декартовые координаты хА,
уА, zA произвольной точки А, принятой за полюс, и
три угла Эйлера ![]() относительно декартовой
системы координат Ах1у1z1, движущеёся поступательно
с полюсом А (для простоты на рис. 4.7 углы Эйлера не показаны). Для
задания движения свободного тела D необходимо задать:
относительно декартовой
системы координат Ах1у1z1, движущеёся поступательно
с полюсом А (для простоты на рис. 4.7 углы Эйлера не показаны). Для
задания движения свободного тела D необходимо задать:
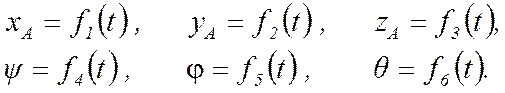 (4.13)
(4.13)
Уравнения (4.13) называются уравнениями свободного
движения твердого тела. Из (4.13) следует, что если зафиксировать углы
Эйлера ![]() , то тело D движется
поступательно как выбранный полюс А, а если мысленно остановить полюс А,
то тело D совершает сферическое движение вокруг этого полюса А.
При свободном движении твердого тела оба эти движения происходят одновременно.
Следовательно, перемещение свободного твердого тела D из одного положения бесконечно близкое складывается
из поступательного перемещения тела вместе с полюсом А и поворота вокруг
мгновенной оси АР, проходящей через этот полюс (рис. 4.7).
, то тело D движется
поступательно как выбранный полюс А, а если мысленно остановить полюс А,
то тело D совершает сферическое движение вокруг этого полюса А.
При свободном движении твердого тела оба эти движения происходят одновременно.
Следовательно, перемещение свободного твердого тела D из одного положения бесконечно близкое складывается
из поступательного перемещения тела вместе с полюсом А и поворота вокруг
мгновенной оси АР, проходящей через этот полюс (рис. 4.7).
Поэтому скорость и ускорение любой точки М свободно движущегося тела складываются из скоростей и ускорений точки М в поступательном движении вместе с полюсом А и из скорости и ускорения точки М в сферическом движении вокруг этого полюса и определяются по формулам:
![]() ,
,
![]() ,
,
где ![]() ,
, ![]() -
скорость и ускорение полюса А,
-
скорость и ускорение полюса А, 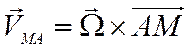 - скорость, а
- скорость, а ![]() - ускорение точки М в сферическом
движении вокруг полюса А.
- ускорение точки М в сферическом
движении вокруг полюса А.
Пример
4.1. Конус с углом при вершине ![]() и
радиусом основания
и
радиусом основания ![]() катится по
неподвижной плоскости без скольжения (рис.4.8). Скорость центра основания
катится по
неподвижной плоскости без скольжения (рис.4.8). Скорость центра основания ![]() . Определить в данный момент времени
угловую скорость
. Определить в данный момент времени
угловую скорость ![]() , угловое
ускорение
, угловое
ускорение ![]() , скорость и
ускорение точки В конуса.
, скорость и
ускорение точки В конуса.
Решить задачу при следующих
данных: ![]() ,
, ![]() 20 см,
20 см, ![]() 60 см/с.
60 см/с.
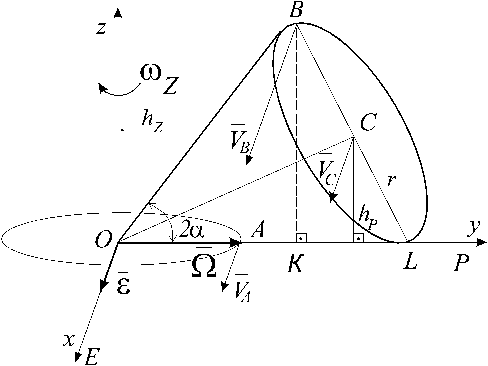
Рис. 4.8
Решение. Конус совершает сферическое движение. Для определения положения мгновенной оси ОР конуса найдем две точки, скорость которых в данный момент времени равны нулю. Такими точками являются точка О и любая точка L касания конуса с неподвижной плоскостью ху. Прямая ОР - образующая конуса, проходящая через точки О и L в каждый момент его движения является мгновенной осью вращения тела (рис. 4.8).
Для определения мгновенной угловой скорости ![]() конуса
опустим из точки С на ось ОР перпендикуляр
конуса
опустим из точки С на ось ОР перпендикуляр ![]() .
Тогда согласно (4.6)
.
Тогда согласно (4.6)
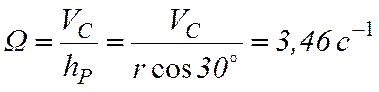 .
.
Найдем скорость точки В, опустив из нее
перпендикуляр ВК на мгновенную ось ОР равный по величине 2![]() (рис.
4.8):
(рис.
4.8):
![]() см/с.
см/с.
Поскольку для точки С скорость ![]() –
постоянна по величине, то вектор мгновенной угловой скорости
–
постоянна по величине, то вектор мгновенной угловой скорости ![]() также
является постоянным по модулю. При качении конуса по неподвижной плоскости ху
конец вектора
также
является постоянным по модулю. При качении конуса по неподвижной плоскости ху
конец вектора ![]() – точка А описывает окружность радиуса
– точка А описывает окружность радиуса ![]() (рис.
4.8). Согласно (4.4)
(рис.
4.8). Согласно (4.4)
![]() , (4.14)
, (4.14)
где
![]() –
угловая скорость вращения конуса вокруг оси Oz. Для вычисления
–
угловая скорость вращения конуса вокруг оси Oz. Для вычисления ![]() проведем из точки С на ось Оz
перпендикуляр
проведем из точки С на ось Оz
перпендикуляр ![]() (рис. 4.8)
(рис. 4.8)
![]() см.
см.
Тогда
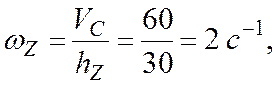
и
из (4.14) 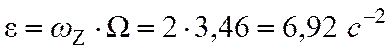 .
.
Для определения ускорения точки В конуса воспользуемся теоремой (4.7):
![]() ,
,
где
![]() 415,7 см/с2.
415,7 см/с2.
![]() 277,1 см/с2.
277,1 см/с2.
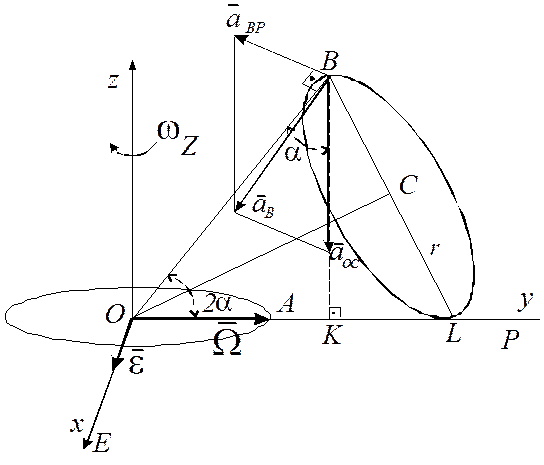
Вектор осестремительного ускорения ![]() направлен
из точки В к мгновенной оси вращения ОР (рис. 4.9). Вектор
вращательного ускорения
направлен
из точки В к мгновенной оси вращения ОР (рис. 4.9). Вектор
вращательного ускорения ![]() перпендикулярен плоскости, проходящей через векторы
перпендикулярен плоскости, проходящей через векторы ![]() и
и ![]() .
Вектор полного ускорения точки В –
.
Вектор полного ускорения точки В – ![]() определяется диагональю параллелограмма, построенного
на векторах
определяется диагональю параллелограмма, построенного
на векторах ![]() и
и ![]() как на сторонах, модуль которого
как на сторонах, модуль которого
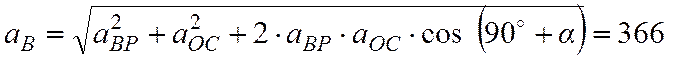 см/с2.
см/с2.
Вопросы для самопроверки
1. Что необходимо задать, чтобы задать сферическое движение твердого тела?
2. Что называется мгновенной осью вращения тела?
3. Как определяется направление вектора углового ускорения тела в данный момент времени при сферическом движении?
4. Как определяется модуль и направление скорости точки тела при сферическом движении?
5. Как определяется модуль и направление ускорения точки тела при сферическом движении?
6. Сколько степеней свободы имеет тело при сферическом движении?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.