Исходные данные
Рассчитать параболическую однозеркальную антенну с рупорным облучателем, круглым волноводом.
|
Номер группы |
Номер по журналу |
Номер зачётной книжки |
Номер зачётной книжки + номер в журнале группы |
|
Р54-6Б |
8 |
041752 |
10 |
|
Тип антенны, её вид (приёмная или передающая) |
Частота (ГГц)/ Мощность (Вт) |
Ширина ДН по уровню половинной мощности (градусы) |
Уровень боковых лепестков (dB) |
|
Приёмная параболическая однозеркальная антенна с рупорным облучателем |
5,1/25 |
9 |
-20 |
Радиус зеркала определяется исходя из заданной ширины диаграммы направленности, длина фидерной линии передачи берётся равной 4R.
Условные обозначения, используемые в проекте, приведены в таблице 1.3.
|
Наименование |
Условное обозначение |
Единица измерения |
|
Рабочая частота |
|
Гц |
|
Диаметр раскрыва рупора |
|
м |
|
Оптимальная длинна рупора |
|
м |
|
Апертурный коэффициент использования поверхности (КИП) |
|
безразмерная |
|
Диаграмма направленности (ДН) рупорного облучателя |
|
безразмерная |
|
Диаграмма направленности (ДН) антенны в целом |
|
безразмерная |
|
Коэффициент направленного действия (КНД) |
|
безразмерная |
|
Длина волны в вакууме |
|
м |
|
Волновое число |
|
м-1 |
|
Диаметр апертуры зеркала |
|
м |
|
Радиус апертуры зеркала |
|
м |
|
Фокусное расстояние |
|
м |
|
Апертурное распределение поля |
|
м |
|
Коэффициент расширения луча |
|
безразмерная |
|
Точность выполнеия профиля зеркала |
КРЛ |
безразмерная |
|
Коэффициент усиления антенны |
|
безразмерная |
|
Коэффициент полезного действия (КПД) |
|
безразмерная |
|
Критическая длина волны |
|
м |
2 Патентный поиск.
Расчёт антенно-фидерного устройства
Исходя из заданной рабочей частоты, для питания антенны выберем стандартный круглый металлический волновод с внутренними размерами:
![]() мм
мм
![]() мм
мм
Рассчитаем длину волны заданной частоты в свободном пространстве по формуле:
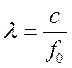 ,
,
где c – скорость света в вакууме; ![]() λ – длина волны в свободном пространстве;
λ – длина волны в свободном пространстве;
![]() - заданная частота.
- заданная частота.
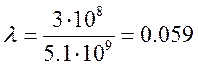 м.
м.
Волновое число
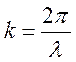
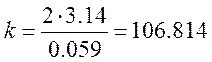
Для наглядности на рисунке изобразим зеркало антенны и её основные геометрические размеры
Определим диаметр и радиус зеркала антенны, исходя из заданной ширины ДН по формуле
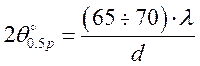 ,
,
откуда, приняв коэффициент в числителе равным 70,
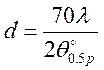
где d – диаметр зеркала
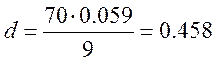 м.
м.
Радиус зеркала
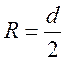
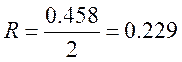 м
м
Длину питающего волновода lф примем равной
![]()
Откуда
![]() м
м
Угол раскрыва параболической антенны в плоскости H ψ0, отсчитываемый от нормали к апертуре рупора, примем равный 55°.
Зная радиус R и угол раскрыва ψ0 зеркала (рисунок 1)
можно вычислить фокусное расстояние ![]() по формуле
по формуле
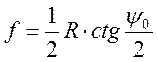
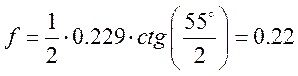 м
м
Найдём параметры облучающего рупора: диаметр рупора и его оптимальную длину.
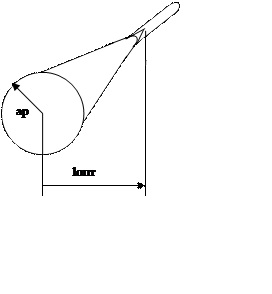 |
Рисунок 2 – Апертурный облучатель в виде конического рупора.
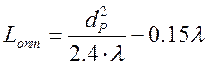
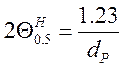 ,
,
отсюда
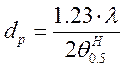
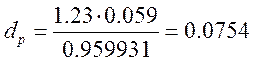 м
м
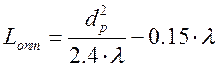
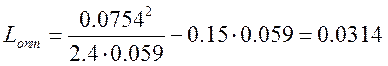 м
м
Выражение для нормированной амплитудой ДН конического рупора
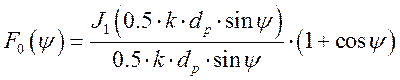 ,
,
где ![]() - функция Бесселя
первого порядка.
- функция Бесселя
первого порядка.
После отражения от зеркала сферическая волна,
исходящая от облучателя, трансформируется в плоскую волну в апертуре зеркала,
диаметром 2R. распределение электрического поля этой волны в
апертуре (![]() ) обладает симметрией относительно
центра апертуры, то есть поле зависит только от координаты
) обладает симметрией относительно
центра апертуры, то есть поле зависит только от координаты ![]() . Апертурное распределение поля
. Апертурное распределение поля ![]() связано с диаграммой направленности
облучателя соотношением
связано с диаграммой направленности
облучателя соотношением
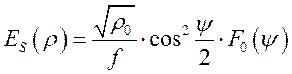
где ![]() - волновое
сопротивление свободного пространства.
- волновое
сопротивление свободного пространства.
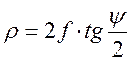 .
.
Диаграмма направленности по полю выражается через ![]() следующим образом
следующим образом
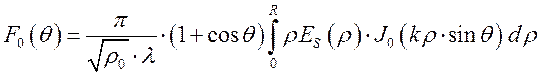 ,
,
где ![]() - функция
Бесселя нулевого порядка.
- функция
Бесселя нулевого порядка.
Нормируем полученную функцию
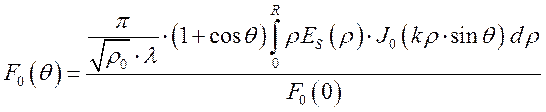 .
.
Диаграмму направленности апертурного поля в логарифмическом масштабе определим по формуле
![]() .
.
График диаграммы направленности антенны в логарифмическом масштабе приведён на рисунке 3.
Изобразим график диаграммы направленности антенны в увеличенном масштабе (рисунок 4). Из этого построения определим ширину ДН по уровню – 3 дБ. Для этого на графике проведём прямую, параллельно оси OX по уровню – 3 и найдём точки пересечения прямой с графиком.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.