Рупорные антенны. Метод исследования рупоров. Коэффициент направленного действия рупорных антенн

Рупорные антенны

     Волноводные излучатели имеют широкую ДН, малый КНД, плохо согласованы со свободным пространством.

Указанные недостатки волноводного излучателя в большой мере устраняются, если к отверстию волновода примкнуть рупор. Так как площадь раскрыва рупора больше площади отверстия волновода, то направленность излучателя намного возрастает. Кроме того, постепенное расширение рупора способствует согласованию волновода со свободным пространством. Например, для волны H₁₀ критическая длина волны λ_кр = 2а возрастает пропорционально широкой стороне а поперечного сечении, а это означает, что волновое сопротивление рупора приближается к 377 ом:

Постепенное увеличение поперечного сечения рупора способствует также затуханию высших типов волн.

Имеется несколько типов рупорных антенн: H-плоскостные секториальные , E-плоскостные секториальные, пирамидальные и конические. Обычно в секториальных и пирамидальных рупорах возбуждается волна Н₁₀, а в конических Н₁₁. Отличаются Н- и Е-плоскостные секториальные рупоры тем, что первые расширяются в плоскостиН ,а вторые – в плоскости Е. В первых

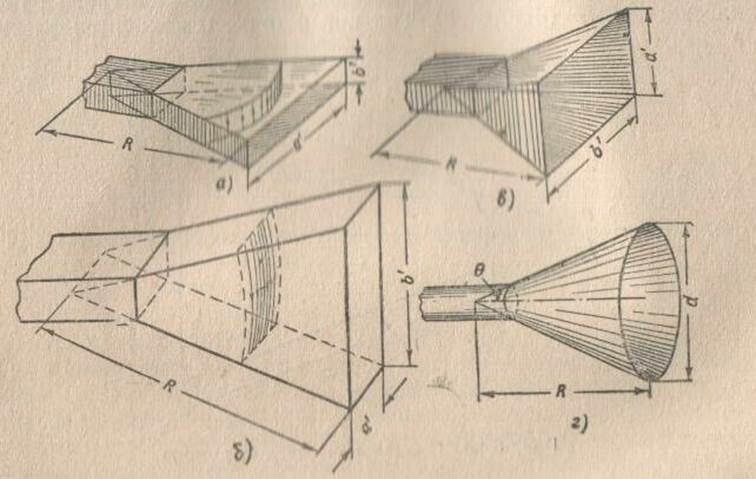
силовые линии электрического поля перпендикулярны широкой стороне раскрыва, а во вторых — узкой. Пирамидальные рупоры расширяются в обеих плоскостях. Волны в любом рупоре несколько отличаютсяот волн в волноводе. Сводятся эти различия к следующему:

1.Увеличение λкр при движении волны к раскрыву рупора вызывает убывание фазовой скорости v до скорости распространения волн с в свободном пространстве:

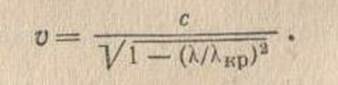
2. В процессе движения волны в секториальном рупоре фронт преобразуется из плоского в цилиндрический а в пирамидальном и коническом рупорах — в сферический. Фазовый центр полученных волн находится в точке пересечения расширяющихся сторон рупора. От этой точки отсчитываются размеры l и R.                

Метод исследования рупоров.

Строгая теория рупорных антенн до сих пор еще не создана. Поэтому для нахождения поля излучения рупора используется апертурный метод. Как и в случае волноводного излучателя, поле на внешней поверхности стенок рупора и питающего волновода принимается равные пулю. Поле в раскрыве полагают равным полю падающей волны в соответствующем сечении бесконечно длинного рупора. Волны высших типов, возникающие вблизи раскрыв, не учитываются. Отраженную волну основного типа обычно также не учитывают в силу хорошего согласования рупора со свободным пространством. Поскольку строгого решения для рупорных антенн нет, то единственным критерием приемлемости апертурного метода расчета служит эксперимент. Для области главного лепестка и ближаиших  к нему боковых лепестков экспериментально снятые ДН хорошо согласуютсяс ДН, рассчитанными апертурнымметодом.

 Исследование секториальных рупоров производится следующим образом. Рупор предполагается бесконечно длинным, стенки его идеально проводящими. Сторонние токи в рупоре отсутствуют. При этих условиях записываются уравнения Максвелла в цилиндрической системе координат. Для Н-секториального рупора используется система координат у, р,φ

Ось у нормальна к плоскости рисунка и проходит через линию пересечения  расходящихся  боковых стенок - вершину рупора. Предполагая, что в питающем волноводе

распространяется волна Н₁₀ ищут в рупоре волну аналогичной структуры, у которой отличны от нуля составляющие Еу, Нφ, Нρ. Остальные составляющие (Ну,Еφ,Еρ) принимаются равными нулю.

 Граничные условия будут

Соотношения указанные выше позволяют построитькартину распределения поля в рупоре. Сравнивая поля в рупоре и питающем его волноводе, можно сделать следующие выводы:

   — Структура поля в рупоре (конфигурация электрических и магнитных силовых линии) сходна со структурой поля в прямоугольном волноводе.

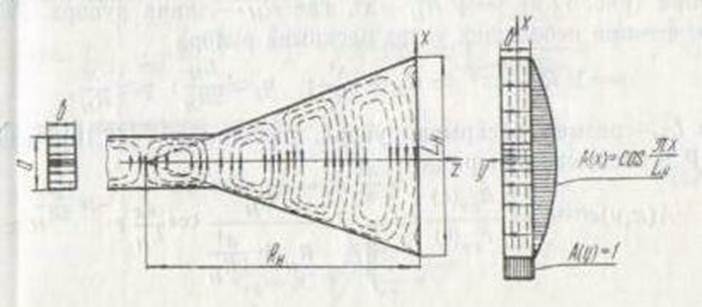
— Фронт волны из плоского (для поперечных составляющих полей) в волноводе превращается в рупоре в цилиндрический.Ось цилиндрической поверхности проходит через вершину рупора.

— По мере удаления от вершины рупора фазовая скорость распространения волны уменьшается и на значительных расстояниях от вершины рупора равна скорости в свободном пространстве. Структура поля при этом приближается к структуре плоской волны, так как при кρ->∞

т.е. продольная составляющая магнитного поля исчезает, а отнощение поперечных составляющих электрического и магнитного полей становится равным волновому сопротивлению свободного пространства. Последнее обеспечивает хорошее согласование Н-рупора со свободным пространством. Практически волна в рупоре становится близкой к ТЕМ-волне на расстоянии порядка несколько длин волн от вершины рупора. Уменьшение фазовой скорости вдоль рупора объясняется увеличением размера рупора в плоскости Н.По этой причине и рупоре бесконечной длины теряет смысл понятие критической длины волны, так как всегда можно найти сечение, для которого данная длина волны короче критической.

Определим теперь АФР в раскрыве рупора конечной длины. Так как вблизи раскрыва волновое сопротивление рупора близко к волновому сопротивлению свободного пространства,то отражения от раскрыва малы. Поэтому можно пренебречь не только высшими типами волн, которые при приближенном рассмотрении учесть невозможно, но и отраженной волной. 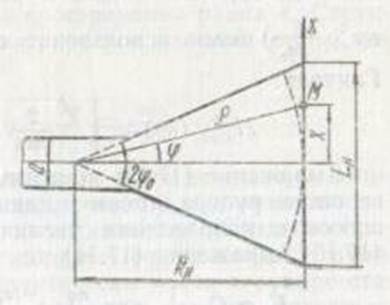При этом можно считать, что поле в раскрыве определяется бегущей от вершины рупора волной. Для произвольной точки М в раскрыве рупора                                         длина рупора. Учитывая, что при небольших углах раскрыва рупора

Как видно амплитудное распределение в раскрыве рупора такое же, как и в прямоугольном волноводе, а фаза вз изменяется по квадратичному закону.

      Амплитудно-фазовое распределение разделяющееся:    

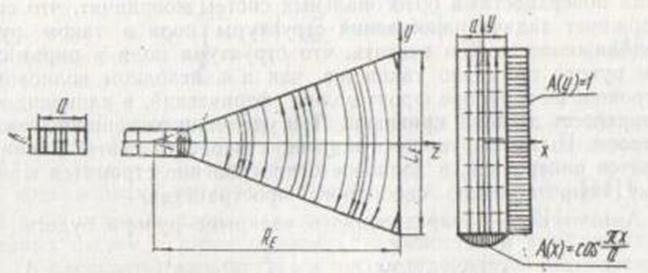
                                               Е-секториальный рупор.

Методика исследования аналогична изложенной выше. Используется цилиндрическая система координат х,ρ,φ. Ось х нормальна к плоскости рисунка и проходит через вершину рупора, р и φ—полярные координаты в плоскости рисунка. В этой системе координат отыскивается решение уравнений поля, для которого отличны от нуля составляющие поля Еφ, Нх, Нρ. Составляющие Ех, Еρ, Нφпринимаются равными нулю.  

Выражения для составляющих поля имеют вид:

      Также,как и в  случае Н-рупора, структура поля в Е-рупоре сходна со структурой поля и питающем волноводе, фронт волны — цилиндрический. Однако в отличие от Н-рупора фазовая скорость распространения волны вдоль Е-рупора остается неизменной, равной фазовой скорости в волноводе. Это связано с тем,что размер рупора в магнитной плоскости не изменяется. При удалении от вершины рупора структура поля не меняется, волна не становится поперечной, волновое сопротивление остается постоянным, равным волновому сопротивлению волновода. Поэтому отражения от раскрыва значительно больше, чем в случае Н-рупора, т.е. Е-рупор хуже согласован со свободным пространством, чем Н-рупор. Тем не менее и в этом случае отраженной волной обычно пренебрегают. При этом получаем следующее приближенное выражение для АФР в раскрыве Е-рупора:

В Н-плоскости изменяется только амплитуда    (по косинусоидальному закону), в Е-плоскости—только фаза    (по квадратичному закону).             

                                                 Диаграммы направленности.

ЗнаяАФР в раскрыве, можно,определить поле излучения различных типов рупоров.

Рассмотрим для примера пирамидальный рупор. Приближенно раскрыв можно представить как систему одинаково ориентированных излучателей Гюйгенса. Тогда имеем

Гак как фаза изменяется по квадратичному закону, то рупорные антенны, строго говоря, не имеют фазового центра. Вычисления приводит к довольно громоздкому комплексному выражению, содержащему интегралы Френеля. В двух главных плоскостях получаем такие же ДН, как и для линейных систем с равномерным (Е-плоскость) и косинусоидальным (Н-плоскость) амплитудным распределением и квадратичным распределением фазы.

Если искажения фазы в раскрыве невелики (меньше  π/8 в Е-плоскости и меньше π/4 в Н-плоскости), то приближенно можно считать раскрыв синфазным с амплитудным распределением А1(х)=соs(πх/Lн), А2(у)=1. При этом ДН в главных плоскостях будут такими же, как и для прямоугольного волновода:

Диаграммы направленности секториальных и конических рупоров находят аналогично изложенному выше. При малых фазовым искажениях ДН таких антенн имеют такой же вид, как и для прямоугольного или круглого волноводов соответственно.       

                                                      КНД рупорных антенн.

Графики  дают зависимость КНД Н-секториального и Е-секториального рупоров от относительной величины размера раскрыва                                    при различных значениях относительной длины рупора                                    Значения Dн и Dе, часто называют удельными КНД секториальных рупоров. Эти величины представляют собою КНД секториальных рупров, у которых постоянный размер поперечного сечения (равный b для Н-рупора или а для Е-рупора) равен длине волны. Если этот размер не равен λ, то значения Dн или Dе, полученные из графиков нужно умножить на b/λ (для Н-рупора) или а/λ (для Е-рупора). Характерным для графиков ялвляется наличие максимума КНД при определеаной величине раскрыва. Такой характер графиков объясняется следующим.

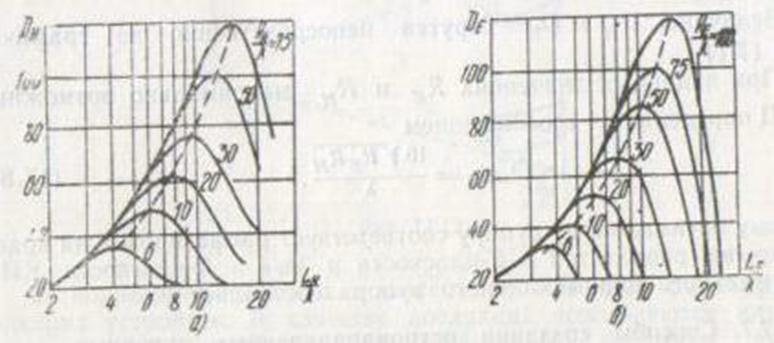
 С увеличением размеров раскрыва КНД должен возрастать. Однако с ростом Lне увеличиваются фазовые искажения поля в раскрыве. Из-за этого рост КНД замедляется и при некотором оптимальном значении, КНД достигает максимума, а затем

падает. Расчеты показывают, что при любой длине R оптимальному рупору соответствует одна и та же величина расфазировки Δφmax на краю раскрыва.