Преобразователи угла в код, построенные по методу последовательного счета, страница 3

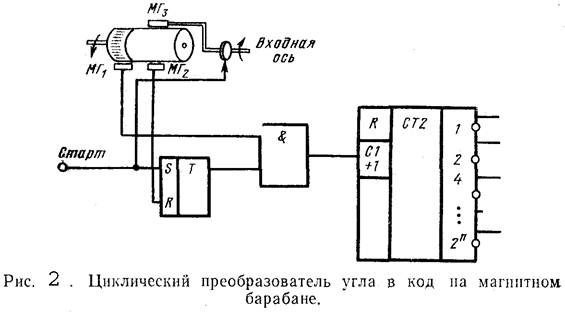
В качестве примера такого АЦП рассмотрим преоб­разователь угла в код на магнитном барабане (рис. 2). Постоянно вращающийся магнитный барабан имеет две дорожки. На первой через равные угловые промежутки нанесены метки, представляющие собой постоянно на­магниченные участки минимального размера, на этой до­рожке расположена магнитная головка МГ₁, выходные импульсы с которой поступают на счетчик. На второй дорожке нет постоянно записанных меток; над этой до­рожкой расположена магнитная головка МГ₃, закреплен­ная на входной оси, угол поворота которой должен быть преобразован в код. Кроме головки МГ₃ над второй до­рожкой расположена неподвижная магнитная головка МГ₂, осуществляющая считывание    выходного сигнала, возникающего при прохождении метки, записанной го­ловкой МГ₃, расположенной под головкой МГ₂.

При подаче на головку МГ₃ старт-импульса на вто­рой дорожке возникает метка, угловое положение ко­торой соответствует текущему значению угла поворота входной оси. Одновременно приход старт-импульса от­крывает схему совпадения и импульсы с головки МГ\ начинают поступать на счетчик. Когда записанная на второй дорожке метка дойдет до неподвижной головки МГ₂, выходной импульс этой головки перебросит триггер в нулевое положение и импульсы с головки МГ₁ пере­станут поступать на счетчик. Таким образом, число им­пульсов, зафиксированных счетчиком, будет пропорцио­нально углу поворота МГ₃, т. е. углу поворота входной оси. В конце каждого цикла метка на второй дорожке стирается и считываются показания счетчика. Точность преобразования зависит от плотности записи меток на первой дорожке и длины этой дорожки (диаметра бара­бана). Характерно, что для обеспечения точности преоб­разования нет необходимости в постоянстве частоты вра­щения барабана, что создает определенные удобства.

Для повышения точности возможны два метода. Первый метод аналогичен методу повышения точности преобразователей временного интервала в код, в кото­ром используются линии задержки. При этом на поверх­ность барабана наносится несколько семейств меток, сдвинутых одна относительно другой на часть кванта и считываемых индивидуальными магнитными головками, связанными с индивидуальными счетчиками. При вто­ром методе, временной интервал между моментами по­ступления сигналов от двух соседних меток разбивается на более мелкие временные интервалы с помощью им­пульсов генератора высокой частоты. В этом случае про­странственная развертка дополняется временной, кото­рая требует постоянства частоты вращения барабана на время между поступлениями сигналов от соседних меток.

Второй группой циклических преобразователей угла в код являются преобразователи с временной разверт­кой. В простейшем варианте такого преобразования угол между началом отсчета и текущим положением оси преобразуется во временной интервал с помощью чув­ствительного элемента, вращающегося с постоянной ско­ростью. Временной интервал преобразуется в цифровой код рассмотренными в гл. 4 методами. Точность такого преобразователя в основном определяется постоянством-частоты вращения чувствительного элемента, а так как частота вращения зависит от ряда внешних факторов, таких как величина питающего напряжения, температу­ра окружающей среды и других, то этот тип преобразо­вателя в простейшем исполнении не обеспечивает вы­сокой точности и сравнительно редко используется.

Широкое распространение нашли циклические преоб­разователи с временной разверткой, у которых исходная угловая величина вначале преобразуется в угол сдвига фазы, который затем преобразуется в код. В этом случае последовательно выполняются преобразования угол–фаза–временной интервал–код. Для осуществления преобразования угла поворота оси в сдвиг фаз исполь­зуются фазовращатели, наиболее распространенными из которых являются индукционные электрические, маши­ны типа вращающихся трансформаторов или сельсинов. У этих машин амплитуда выходного напряжения пере­менного тока, снимаемого с одной пли двух обмоток, про­порциональна синусу или косинусу угла поворота ротора машины. Непосредственное использование этого выход­ного напряжения вызывает необходимость перехода от синусной зависимости к зависимости от угла. Поэтому на практике в качестве фазовращателя используют вра­щающийся трансформатор и снимают два выходных на­пряжения с синусной и косинусной обмоток и пропуска­ют эти напряжения через специальную фазосдвигающую цепочку. В этом случае на выходе фазосдвигающей це­почки удается получить переменное напряжение, имею­щее фазовый сдвиг относительно питающего напряже­ния, пропорциональный углу поворота ротора а_х вра­щающегося трансформатора [14].

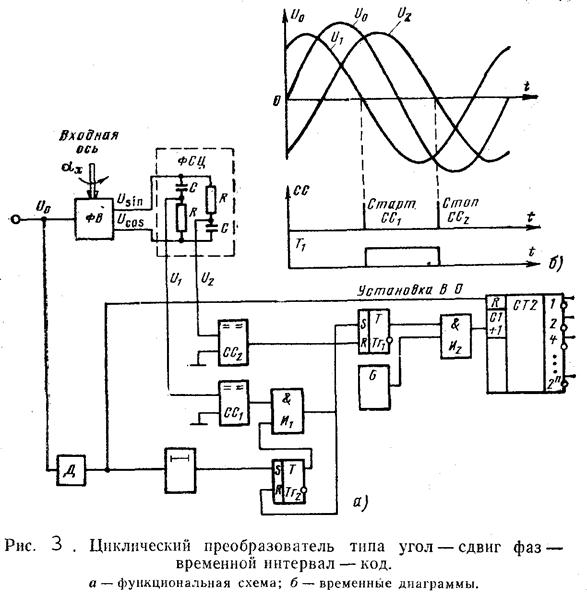
Функциональная схема такого преобразователя при­ведена на рис. 3, а. На выходе вращающегося транс­форматора получаются два напряжения:

,                    [1]

,                    [2]

где  – амплитуда питающего напряжения;  – ко­эффициент трансформации во вращающемся трансфор­маторе;  – частота питающего напряжения.

Если параметры элементов фазосдвигающей цепочки подобраны так, чтобы , то общий фазовый сдвиг между напряжениями  и  [14]:

.

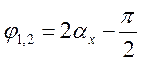Этот фазовый сдвиг с помощью схем сравнения (компараторов)   и  преобразуется во временной ин­тервал. Для этого компараторы определяют    моменты времени, в которые эти напряжения проходят через нуль в определенном направлении, например, как это показано на рис. 3, б, из положительной области в отрица­тельную. Временной интервал будет пропорционален сдвигу фаз, а значит, и углу поворота входной оси , Преобразование полученного временного интервала в код может быть осуществлено методами, которые опи­саны в гл. 4.