Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ
Кафедра «Высшей математики»
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
ЗАДАЧА №3
Выполнил:
ст-т гр. Р56-2
Р.А. Матюшев
Проверил:
Н.В. Кузоватова
Красноярск 2008
Дан тонкий однородный
стержень длиной 0<x<3, боковая поверхность которого теплоизолирована.
Найти распределение температуры u(x,t) в стержне, если его начальная температура u(x,0)=2x-3, левый
конец стержня теплоизолирован, правый поддерживается при постоянной температуре
u2=![]() .
.
Постановка задачи, одномерное уравнение теплопроводности, граничные и начальные условия:
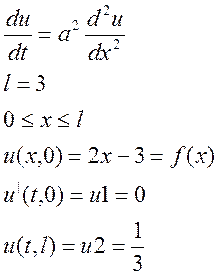
Рассмотрим все возможные случаи:
Однородное уравнение теплопроводности с неоднородными краевыми условиями:
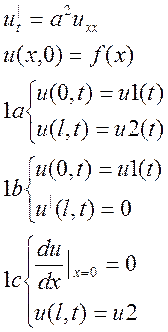
граничные условия неоднородные, следовательно, метод Фурье не применим.
Сведем задачу с однородными краевыми условиями:
![]()
W(x) удовлетворяет стационарным уравнениям теплопроводности:
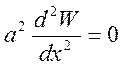
W(x) должно удовлетворять краевым условиям (1a,1b,1c)
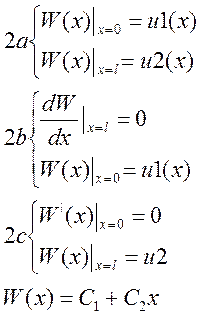
C1 и C2 определяются из условий (2a,2b,2c)
Для (2a,2b,2c) имеем:
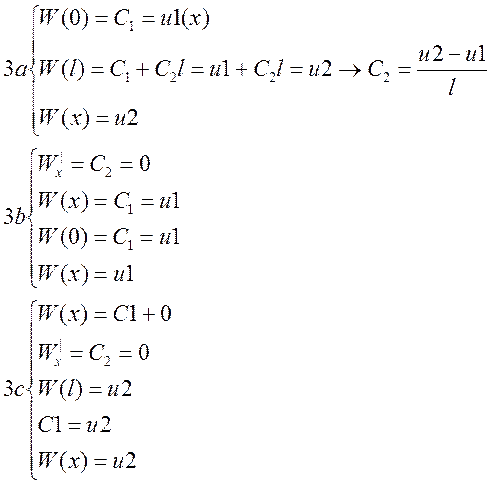
Перейдем к решению непосредственно нашей задачи:
W(x) должна удовлетворять уравнению с следующими краевыми условиями:
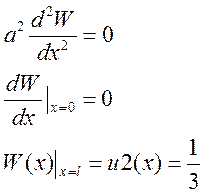
Решение этой задачи находится в виде (так как для многочлена не более второй степени вторая производная может равняться нулю):
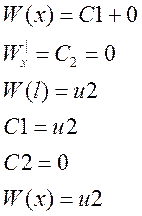
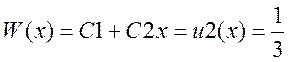
Для нахождения второй функции v(x,t) поставим задачу с однородными краевыми условиями и решим ее:
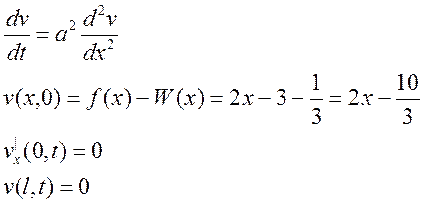
Решение этой задачи найдем в виде:
![]()
Дифференцируем его по t и по х два раза:
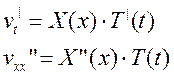
Подставим в исходное и получим:
![]()
Разделим переменные:
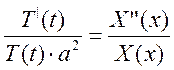
Это равенство возможно, только если обе части не зависят от переменных и равны константе. Обозначим ее через минус лямбда:
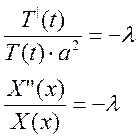
Приведем к бездробному виду:
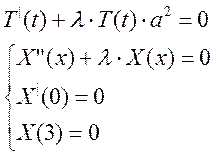
Накладываем граничные условия. Так как функция u(x,t) не может обращаться в ноль, то следовательно функция T(t) не может равняться нулю, как следствие граничные условия накладываются только на Х(х):
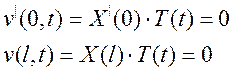
С учетом этого находим X(x) из уравнения:
![]()
Это дифференциальное уравнение второго порядка с постоянными коэффициентами без правой части. Составим для него характеристическое уравнение и решим его:
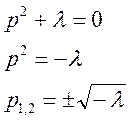
Рассмотрим все возможные решения:
- Случай первый, корни
действительные, кратные (![]() = 0):
= 0):
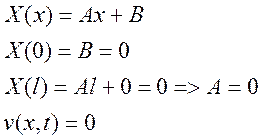
То есть получается тривиальное решение.
- Случай второй, корни
действительные разные (![]() < 0):
< 0):
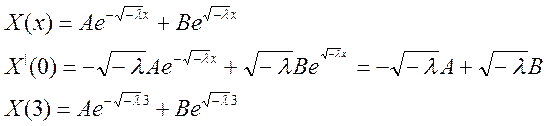
Подставив в это равенство краевые условия, получим что коэффициенты А и В будут равны нулю, так как сумма двух положительных функций равняется нулю только если они обе равны нулю. Другими словами, также получаем тривиальное решение.
![]()
- Случай третий, корни
комплексно-сопряженные (![]() > 0):
> 0):
Решение будет иметь вид:
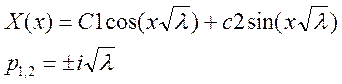
Находим собственные значения, подставив граничные условия:
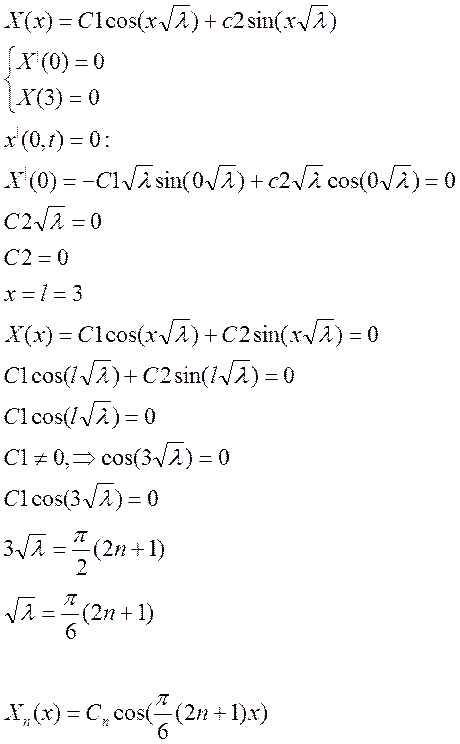
Таким образом, нетривиальное решение получается только в случае, если корни комплексно-сопряженные, и в нашем случае имеет вид:
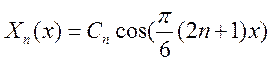
Решаем уравнение ![]() , это уравнение с разделяющимися
переменными
, это уравнение с разделяющимися
переменными
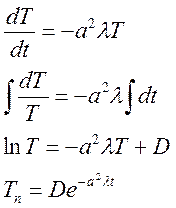
Находим непосредственно функцию v(x,t) по следующей формуле:
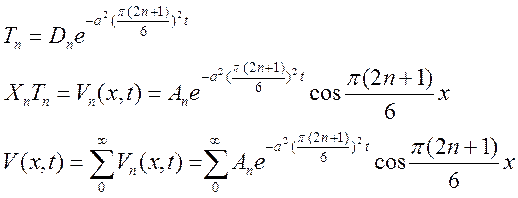
Для V(x,t) подставим начальные условия
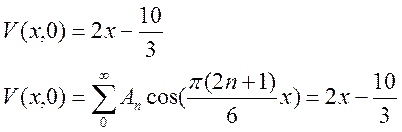
Это есть разложение функции 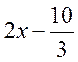 в ряд Фурье по косинусам,
следовательно:
в ряд Фурье по косинусам,
следовательно:
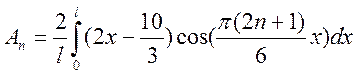
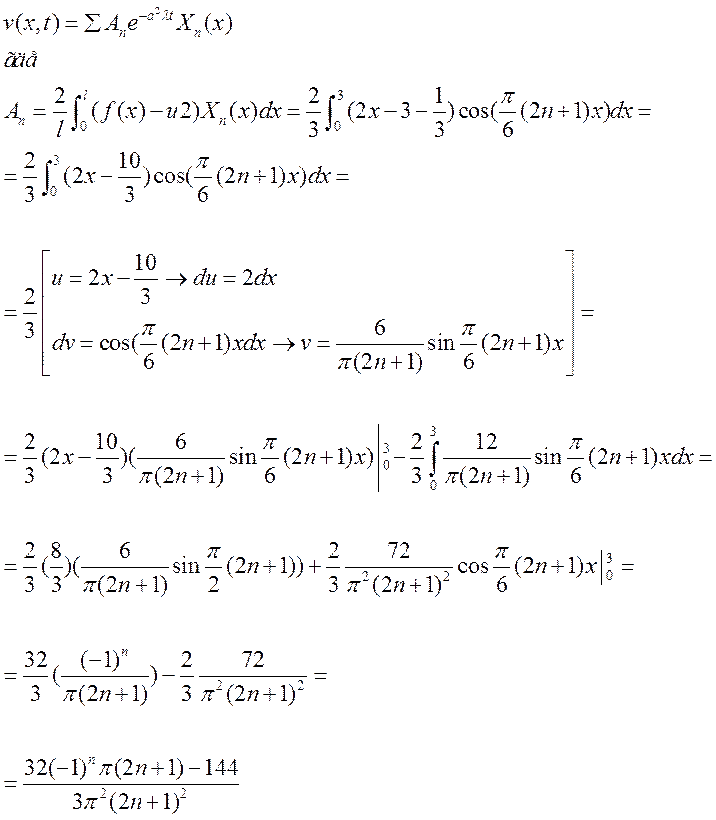
![]()
![]()
![]()
Искомая функция:
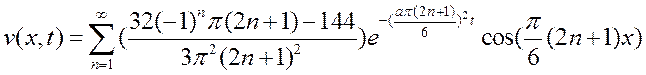
Решение, как сумма двух, выше найденных функций:
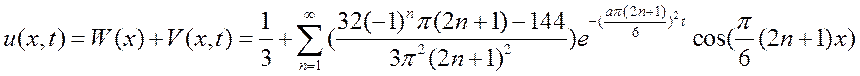
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.