ОПРЕДЕЛЕНИЕ ПРИВЕДЕННОГО МОМЕНТА ИНЕРЦИИ
ШАРНИРНО-РЫЧАЖНЫХ МЕХАНИЗМОВ
ЭКСПЕРИМЕНТАЛЬНЫМ МЕТОДОМ
Цель работы - ознакомиться с методикой экспериментального определения приведенного момента инерции шарнирно-рычажных механизмов.
Краткие теоретические сведения
Приведенный момент инерции плоского шарнирного механизма, имеющего сравнительно малые упругие деформации, зазоры и трещины в кинематических парах, можно определить экспериментальным способом без разборки.
Воздействуем на механизм силой F, которая меняется по периодическому закону. Частота возмущающей силы регулируется при помощи специального устройства. Механизм доводится до резонанса, когда частота собственных колебаний К механизма совпадает с частотой возмущающей силы. При резонансе можно определить период колебаний Т, а затем рассчитать приведенный момент инерции Jnp,
Динамическая модель механизма представляется в виде приведенной массы т„р, закрепленной на упругих элементах, жесткость которых
С = С\ +С2 (рис. 13.1).
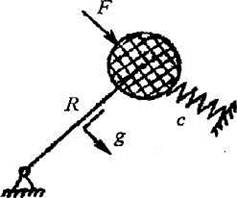 Дифференциальное уравнение вынужденных колебаний
рассматриваемой системы при отсутствии трения имеет вид [6]
Дифференциальное уравнение вынужденных колебаний
рассматриваемой системы при отсутствии трения имеет вид [6]
где q- обобщенная координата (перемещение) массы тпр; Asinωt -возмущающая сила амплитуды А и частоты ω.
|
Рис. 13.1 |
Преобразуем уравнение (13.1):
q + k2q= Bsinωt, (13.2)
где к = (ci+c2)/mnp-частота собственных колебаний механизма; В=А/ттр.
Решение уравнения (13.2) равно сумме (согласно теории дифференциальных уравнений) общего и частного решений. Ограничимся частным уравнением, описывающим вынужденные колебания [6]:
(13.3)
q = Hsinωt,
где Н - амплитуда вынужденных колебаний. Подставив (13.3) в (13.2), получим
Н = В/(к2-ω2).
Явление резонанса наступает при совпадении частот собственных и вынужденных колебаний, т. е. при к = ω. В этом случае Н —► ∞. Для режима резонанса имеем
(13.4)
л[(с1+с2)/тпр =ω = 2π / T
Здесь T- период вынужденных колебаний,
T=60/n ,
где п – резонансная частота, мин'1. Из уравнения (13.4) следует, кг,
mпр =T 2(c1 +c2)/(4π2)
Величина приведенного момента инерции Jnpзависит от радиуса Rмаятника, к которому приведена масса [1],кг-м2:
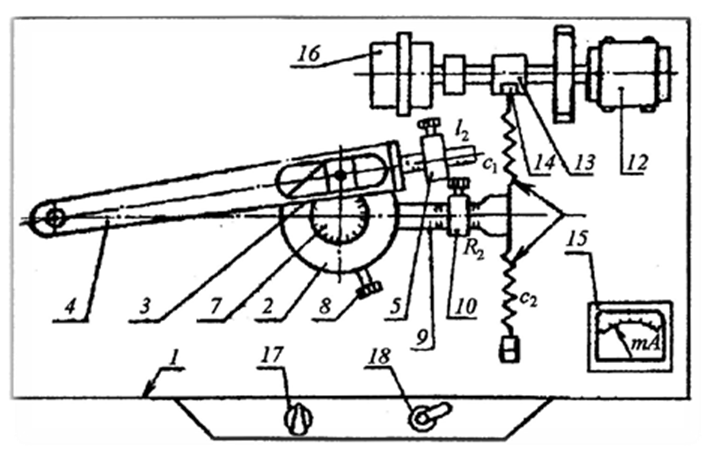
Практическая часть
|
Схема механизма |
|
|
n, мин-1 |
Показания прибора I, мА |
|
300 400 600 800 1000 200 |
6 12 29 47 69 93 |
С1 = 157; С2 = 158; l2 = 0,28м; R2 = 0,9м.
|
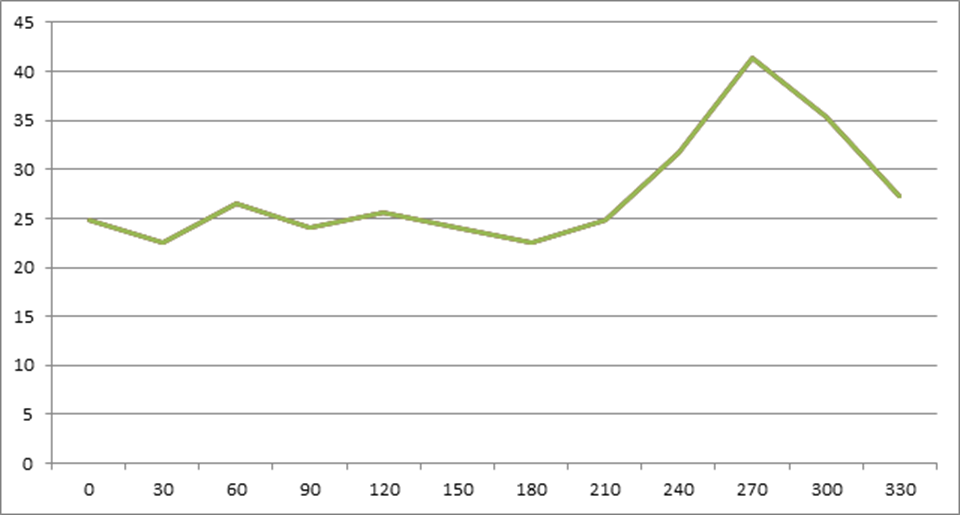
Угол поворота кривошипа |
Схема механизма |
||||
|
I, мА |
n, мин-1 |
Т, с *10-2 |
mпр, кг *10-2 |
Jпр, кг*м2 *10-3 |
|
|
0 |
67 |
971,0 |
6,18 |
3,07 |
24,81 |
|
30 |
70 |
1014,5 |
5,91 |
2,78 |
22,50 |
|
60 |
65 |
942,0 |
6,37 |
3,27 |
26,49 |
|
90 |
68 |
985,5 |
6,09 |
2,97 |
24,05 |
|
120 |
66 |
956,5 |
6,27 |
3,17 |
25,65 |
|
150 |
68 |
985,5 |
6,09 |
2,97 |
24,05 |
|
180 |
70 |
1014,5 |
5,91 |
2,78 |
22,50 |
|
210 |
67 |
971,0 |
6,18 |
3,07 |
24,81 |
|
240 |
59 |
855,1 |
7,01 |
3,91 |
31,70 |
|
270 |
52 |
753,6 |
7,96 |
5,11 |
41,37 |
|
300 |
54 |
782,6 |
7,67 |
4,73 |
35,40 |
|
330 |
64 |
927,5 |
6,47 |
3,37 |
27,31 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.