Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ
Кафедра «ТиКМС»
ЛАБОРАТОРНАЯ РАБОТА №7
ОПРЕДЕЛЕНИЕ ОСНОВНЫХ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ ЗУБЧАТЫХ КОЛЕС
Выполнили:
ст-ты гр. РФ06-02
Р.А. Матюшев
И.И. Костев
Проверил:
Е.Г. Синенко
Красноярск 2008
Цель работы: ознакомиться с практическими методами определения основных параметров зубчатых колес.
Краткие теоретические сведения
Основными параметрами зубчатого колеса с эвольвентным профилем зубьев являются: модуль m, число зубьев z, угол зацепления a, величина смещения инструментальной рейки при нарезании зубчатого колеса. Число зубьев, диаметры окружностей вершин и впадин зубьев можно измерить непосредственно, остальные параметры вычисляют в результате расчета.
Подсчитав число зубьев z, нетрудно определить модуль зацепления, используя свойство эвольвенты - нормаль в любой точке эвольвенты является касательной к основной окружности. Поэтому при охвате нескольких зубьев колеса губками штангенциркуля (размер АВ, рис. 1) линия АВ будет касательной к основной окружности и нормальной профилям зубьев.
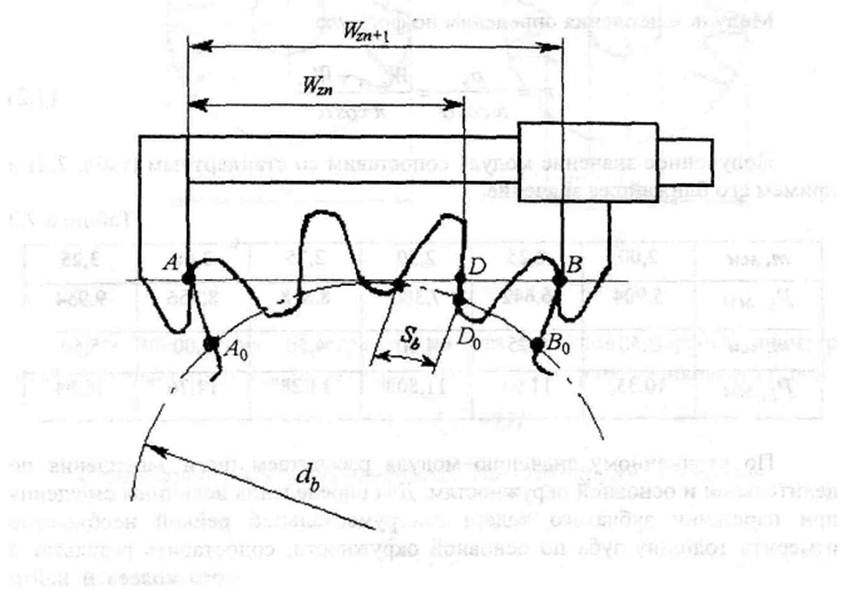
рис. 1
Если отрезок АВ катить по основной окружности, то по свойству эвольвенты точка А придет в точку Aо, тока В - в точку Во и точка D - в точку Dо. Тогда
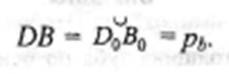
Таким образом, измерив вначале длину общей нормали Wzn,
соответствующей zn - зубьям, а затем размер Wzn+1, охватив губками
штангенциркуля на один зуб больше, шаг по основной окружности
определим как разность двух измерений:
pb = Wzn+1 - Wzn (1)
Это выражение действительно только в том случае, когда губки штангенциркуля касаются эвольвентной части профиля зуба.
Чтобы не возникло кромочного контакта, необходимо правильно выбрать zn (табл. 1).
Таблица 1
|
Число зубьев колеса |
12-18 |
19-27 |
28-36 |
37-45 |
46-54 |
55-63 |
64-72 |
73-81 |
|
zn |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Модуль зацепления определим по формуле
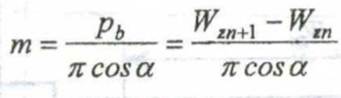 (2)
(2)
Полученное значение модуля сопоставим со стандартным
(табл. 2) и
примем его ближайшее значение.
Таблица 7.2
|
m, мм |
2,00 |
2,25 |
2,50 |
2,75 |
3,00 |
3,25 |
|
pb,мм |
5,904 |
6,642 |
7,380 |
8,818 |
8,856 |
9,954 |
|
m, мм |
3,50 |
3,75 |
4,00 |
4,50 |
5,00 |
5,50 |
|
pb, мм |
10,33, |
11,07 |
11,808 |
13,28 |
14,76 |
16,84 |
По уточненному значению модуля рассчитаем шаги зацепления по делительной и основной окружностям. Для определения величины смещения при нарезании зубчатого колеса инструментальной рейкой необходимо измерить толщину зуба по основной окружности, сопоставить результат с расчетным значением той же толщины зуба для нулевого колеса и найти коэффициент смещения инструментальной рейки:
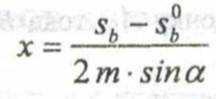 (3)
(3)
где Sb = Wzn+1 – zn*pb) - толщина зуба по основной окружности данного колеса;
Sb0 = m*(π + z*inva) соsа - толщина зуба по окружности зубчатого колеса, нарезанного при х = 0; а = 20°; inv 20° = 0,0149.
При проведении обмера зубчатых колес необходимо измерить также диаметры окружностей выступов da и впадин df.
Если число зубьев шестерни z четное, то оба диаметра могут быть непосредственно измерены штангенциркулем (рис. 2) При нечетном числе зубьев измерение проводится по схеме, изображенной на рис. 3.
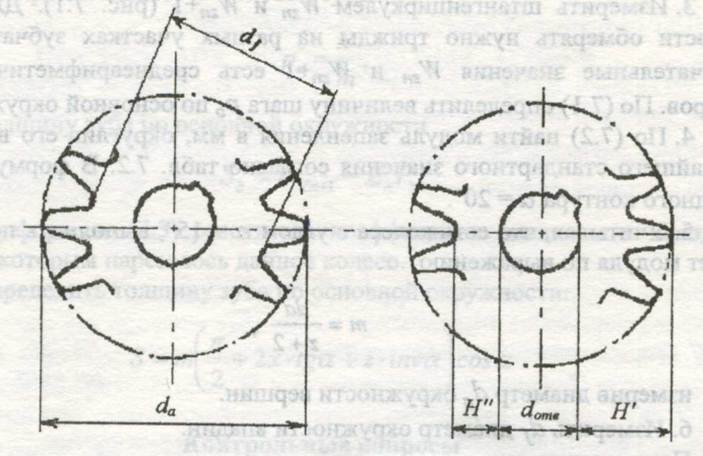
рис. 2 рис. 3
Для определения диаметра окружности выступов измеряется диаметр отверстия шестерни (dотв) и размер Н/. Тогда диаметр окружности выступов
da = dотв + 2 Н/
Совершенно аналогично измеряется диаметр окружности впадин:
df = dотв + 2 Н//
Зная диаметр окружности выступов, можно определить коэффициент высоты зуба нулевого колеса:
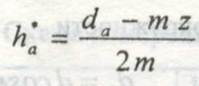
Для проведения этой работы необходимо иметь набор зубчатых колес разных модулей и с разным количеством зубьев и измерительный инструмент – штангенциркуль.
Экспериментальная часть:
1) Число зубьев z=49
2) Определение шага и модуля зацепления
|
№ измерения |
Wzn+1, мм |
Wzn, мм |
|
|
1 |
78 |
67 |
z*n = 6 |
|
2 |
78 |
67 |
|
|
3 |
78 |
67 |
|
|
Среднее |
78 |
67 |
Шаг зацепления по основной окружности: pb=Wzn+1-Wzn=78-67=11 мм
Модуль: m=pb/πcosα=11/2.95=3.72 мм
Уточненный модуль: m=3.75 мм
Шаг зацепления по делительной окружности: p=πm=11.706 мм
3) Диаметр делительной окружности: d=mz=182.58 мм
4) Диаметр основной окружности: db=dcosα=171.569 мм
5) Определение действительной толщины зуба по основной окружности:
Sb=Wzn+1-znpb=12 мм
6) Расчет толщины зуба по основной окружности нулевого колеса: S0b=m(π/2+z*invα)cosα=8.056 мм
7) Определение коэффициента смещения: x=(Sb-S0b)/2msinα=1.547
8) Определение толщины зуба по основной окружности: Sb=m(π/2+2xtgα+z*invα)cosα= 12 мм
9) Определение диаметров окружностей выступов da и впадин df колеса:
|
№ измерен. |
dотв, мм |
H’, мм |
da, мм |
H’’, мм |
df, мм |
Расчетные формулы при нечетном числе z |
|
1 |
36 |
84 |
204 |
74 |
184 |
da=dотв+2H’ |
|
2 |
36 |
84 |
74 |
|||
|
3 |
36 |
84 |
74 |
df=dотв+2H’’ |
||
|
Среднее |
36 |
84 |
74 |
10) Определение коэффициента головки зуба нулевого колеса:
h*a=(da-d)/2m=2.874
11) Определение высоты зуба:
H=H’-H’’=10 мм
Вывод: ознакомились с практическими методами определения основных параметров зубчатых колес.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.