

|
|
|
Исходные данные: |
|
|
|
- истинное значение измеряемой величины |
|
|
|
- дисперсия для нормального закона распределения |
|
|
|
- число итерационных циклов |
|
Формируем погрешность, вносимую в наши измерения, она складывается из суммы двух случайных величин, распределенных по равномерному и нормальному законам соответственно: |
|
|
|
где функция runif формирует 100 случайных чисел, распределенных по равномерному закону в интервале от -1 до 1; функция rnorm формирует 100 случайных чисел, распределенных по нормальному закону с нулевым средним и дисперсией s. |
|
В результате, получаем массив случайных чисел с матожиданием, равным x0, и определенной погрешностью, вносимой в наши измерения: |
|
|
|
Массив ста случайных чисел и погрешностей см. таблицы 1, 2 в приложении 1. |
|
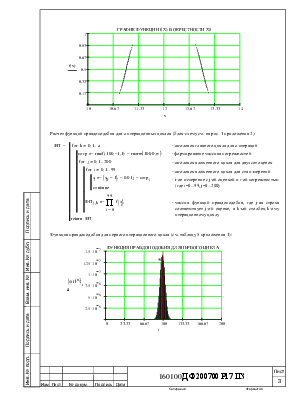
Плотность распределения суммарной погрешности определяется выражением: |
|
|
|
где erf() – предопределенная MathCAD-функция для вычисления интеграла вероятностей (функция ошибок, функция Крампа), в качестве своего аргумента она получает сгенерированное число x, а сама функция центрирована относительно x0. |
|
|
|
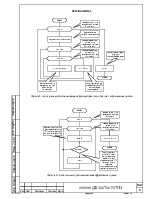
Расчет функций правдоподобия для z итерационных циклов (блок-схему см. на рис. 1 приложения 2): |
|
|
|
- заголовок главного цикла для z итераций |
|
- формирование массива погрешностей |
|
- заголовок вложенного цикла для двухсот оценок |
|
- заголовок вложенного цикла для ста измерений |
|
- i-ое измерение с j-ой оценкой и i-ой погрешностью (где i=0...99, j=0...200) |
|
- массив функций правдоподобия, где j-ая строка соответствует j-ой оценке, а k-ый столбец k-ому итерационному циклу |
|
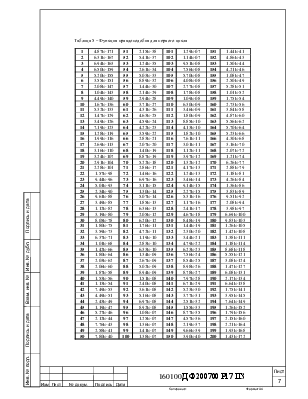
Функция правдоподобия для первого итерационного цикла (см. таблицу 5 приложения 1): |
|
|
|
Оценки, соответствующие максимумам функций правдоподобия (блок-схему см. на рис. 2 приложения 2): |
|
|
|
- заголовок главного цикла для z столбцов-итераций |
|
- заголовок вложенного цикла для i строк-оценок |
|
- элемент i,k массива функций правдоподобия приравнивается к вспомогательной переменной Fp |
|
- если Fp оказывается равной максимуму k-ого столбца FP, то номер этого максимума присваивается переменной est |
|
- возвращаются оценки, соответствующие est-ым элементам z столбцов массива FP |
|
|
|
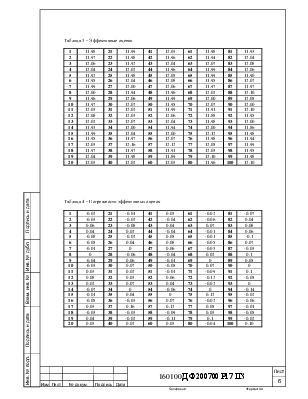
Массив эффективных оценок и погрешностей оценок см. таблицы 3, 4 в приложении: |
|
Среднеквадратичная и среднеарифметическая погрешности оценки: |
|
|
|
|
|
Погрешность оценки среднеарифметического значения: |
|
|
|
|
|
|
|
Погрешность центра рассеяния: |
|
|
|
|
|
|
|
Погрешность медианы оценки: |
|
|
|
|
|
|
|
Исходя из полученных данных, можно сделать вывод, что наиболее эффективной оценкой является та, которая получена методом максимума функций правдоподобия, так как среднеквадратичное отклонение погрешности этой оценки минимально. |
|
Разность между эффективной оценкой и истинным значением измеряемой величины есть погрешность оценки: |
ПРИЛОЖЕНИЕ 1
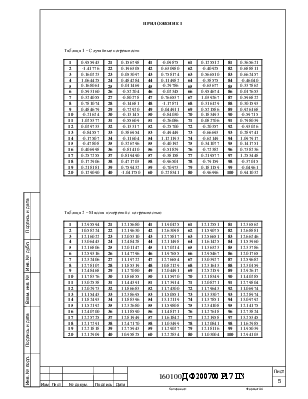
Таблица 1 – Случайные погрешности
|
1 |
0.955943 |
21 |
0.156798 |
41 |
-0.09875 |
61 |
0.125512 |
81 |
0.365621 |
|
2 |
-1.41776 |
22 |
0.196305 |
42 |
0.630980 |
62 |
-0.40925 |
82 |
0.688811 |
|
3 |
0.160223 |
23 |
0.053097 |
43 |
0.758174 |
63 |
0.566510 |
83 |
0.662457 |
|
4 |
1.064425 |
24 |
0.484284 |
44 |
0.114982 |
64 |
-0.38575 |
84 |
-0.46040 |
|
5 |
0.168061 |
25 |
0.011469 |
45 |
-0.29786 |
65 |
-0.63677 |
85 |
0.337862 |
|
6 |
0.593160 |
26 |
-0.52204 |
46 |
-0.02345 |
66 |
0.954674 |
86 |
0.017653 |
|
7 |
0.324055 |
27 |
-0.80278 |
47 |
0.766537 |
67 |
1.039267 |
87 |
0.596822 |
|
8 |
0.781074 |
28 |
-0.14681 |
48 |
-1.17871 |
68 |
0.316129 |
88 |
0.301593 |
|
9 |
0.484679 |
29 |
-0.72920 |
49 |
0.044911 |
69 |
0.521586 |
89 |
0.926168 |
|
10 |
-0.21624 |
30 |
-0.13145 |
50 |
-0.84030 |
70 |
0.183493 |
90 |
-0.59715 |
|
11 |
1.025377 |
31 |
-0.55609 |
51 |
-0.26086 |
71 |
0.082706 |
91 |
0.798039 |
|
12 |
0.029733 |
32 |
-0.13317 |
52 |
-0.25700 |
72 |
-0.20357 |
92 |
-0.93026 |
|
13 |
-0.84557 |
33 |
0.386954 |
53 |
-0.49449 |
73 |
-0.66693 |
93 |
0.289741 |
|
14 |
-0.17507 |
34 |
-0.11604 |
54 |
1.121193 |
74 |
-0.62149 |
94 |
1.097917 |
|
15 |
-0.47808 |
35 |
0.326796 |
55 |
-0.40192 |
75 |
0.341077 |
95 |
0.141751 |
|
16 |
0.406998 |
36 |
-0.81410 |
56 |
-0.51829 |
76 |
-0.72382 |
96 |
0.738236 |
|
17 |
0.257255 |
37 |
0.819490 |
57 |
-0.38158 |
77 |
0.219577 |
97 |
1.253448 |
|
18 |
0.172906 |
38 |
0.471703 |
58 |
-0.96501 |
78 |
-0.79159 |
98 |
-0.37015 |
|
19 |
0.218181 |
39 |
0.759432 |
59 |
-0.70973 |
79 |
0.181159 |
99 |
-0.04961 |
|
20 |
0.129090 |
40 |
-1.041750 |
60 |
0.228341 |
80 |
-0.96996 |
100 |
0.941032 |
Таблица 2 – Массив измерений с погрешностью
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.