Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
КРАСНОЯРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Институт радиоэлектроники
Кафедра: «Радиотехника»
Лабораторный практикум
по ОТиПРС
Выполнила: ст-ка гр. Р51–1М
Руденко Т. Н.
Проверил: Козлов А. В.
Красноярск 2005г.
Лабораторная работа №1
Моделирование и исследование согласованной фильтрации сигнала
![]()
Сформируем исходный импульс:
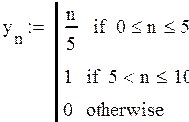
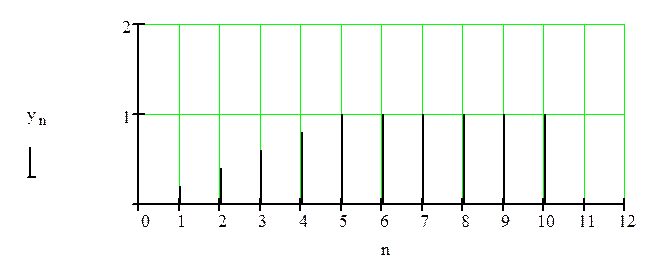
Рисунок 1.1 –Модель импульса заполнения
Код Баркера имеет следующую последовательность:
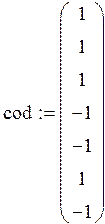
В соответствии с данным кодом составим программу реализации импульсной последовательности:
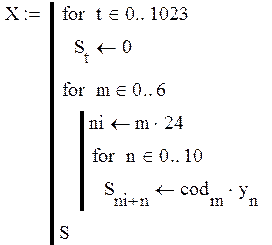
![]()
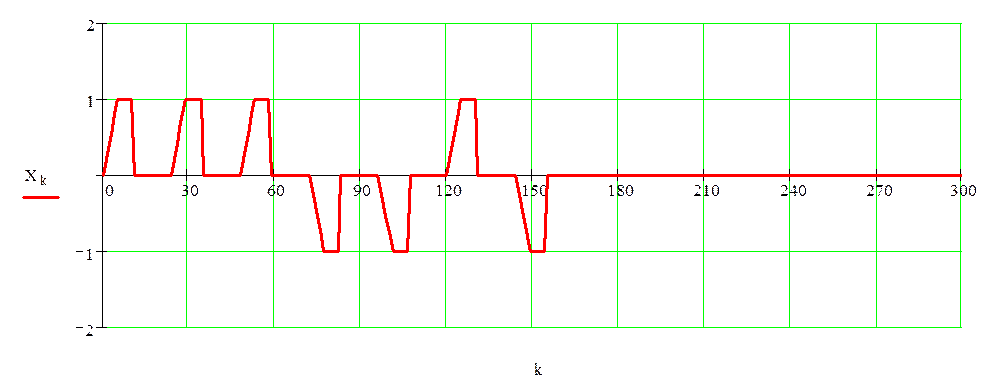
Рисунок 1.2 –Модель импульсной последовательности
Используем стандартную функцию программы Mathcad- FFT(быстрое преобразование Фурье):
|
|
|
|
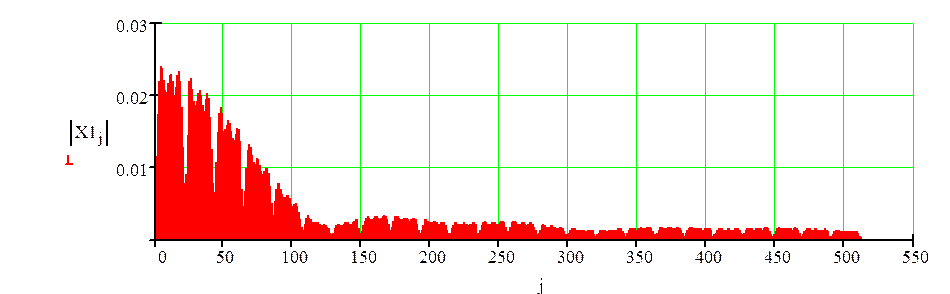
Рисунок 1.3 –Спектр входного сигнала
Сигнал на выходе записывается следующим образом:
|
|
|
|
|
|
|
|
-где IFFT-стандартная функция Mathcad обратного преобразования Фурье.
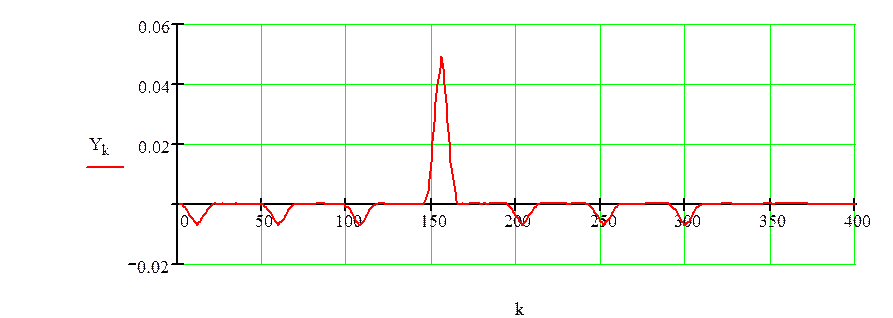
Рисунок 1.4 –Сигнал на выходе
Составим программу для вычисления импульсной характеристики:
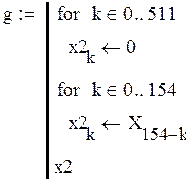
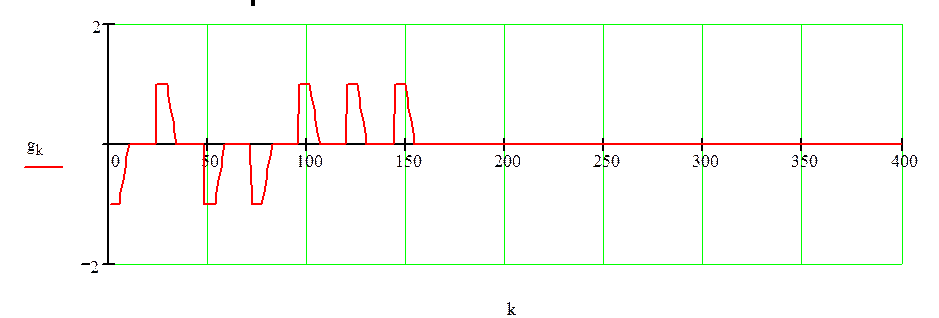
Рисунок 1.5 –Импульсная характеристика
Составим программу для вычисления сигнала на выходе:
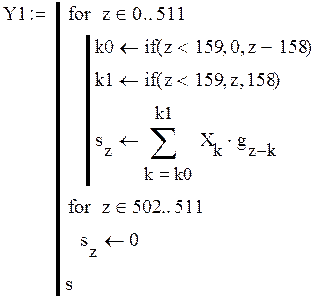
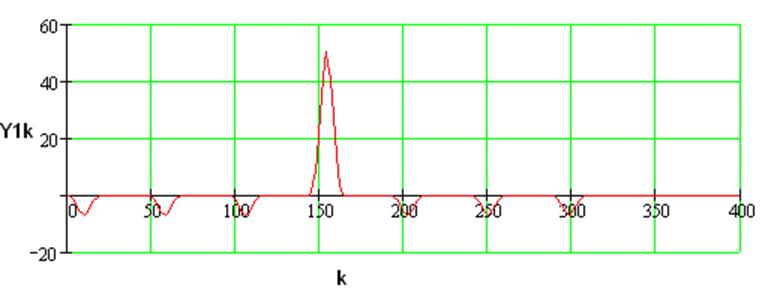
Рисунок 1.6 – Сигнал на выходе
Сопоставление результата FFT преобразования и преобразования с помощью свертки представлено следующим графиком:
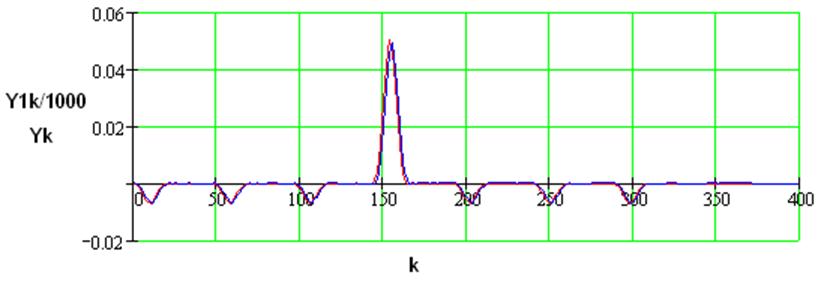
Рисунок 1.7 –Графическое сравнение результатов преобразования Фурье со сверткой
Лабораторная работа №2
Моделирование и исследование согласованной фильтрации зашумленного сигнала
![]()
Сформируем исходный импульс:
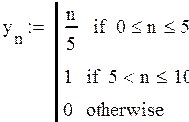
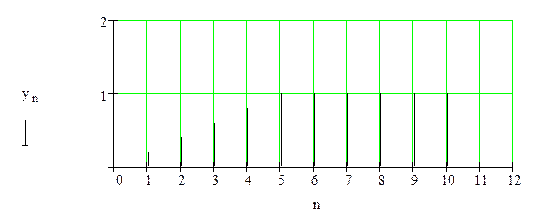
Рисунок 2.1 –Модель импульса заполнения
![]()
В соответствии с кодом Баркера составим программу реализации импульсной последовательности:
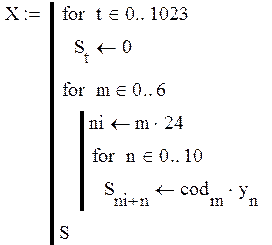
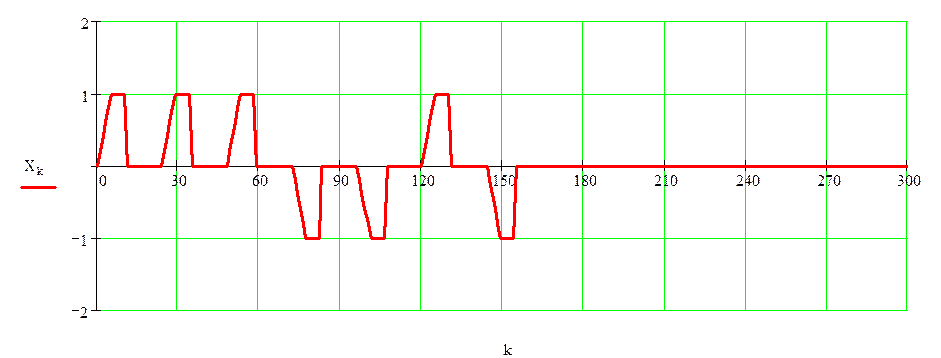
Рисунок 2.2 –Модель импульсной последовательности
Сформируем Гаусовский центрированный шум:
![]() ,
,
где norm - функция нормального распределения MathCad
Программа для формирования модели шума:
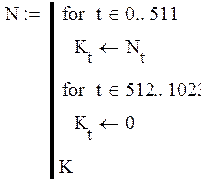
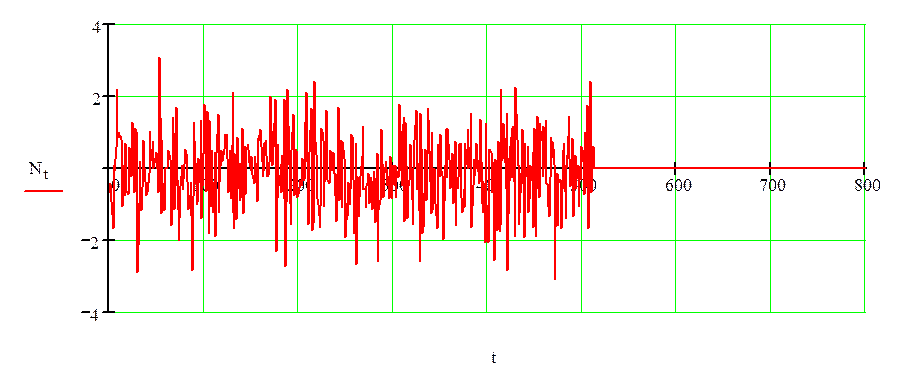
Рисунок 2.3 –Модель шума для вычисления выходного сигнала
Просуммируем сигнал с шумом:
![]()
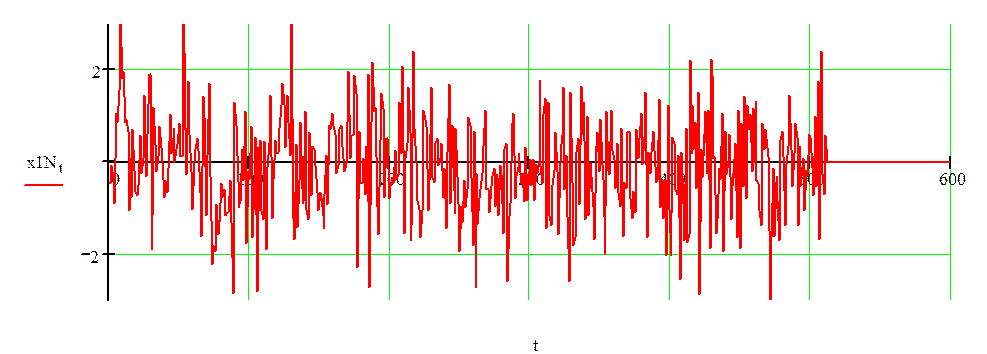
Рисунок 2.4 –Смесь сигнала с шумом
Определим спектр суммарного сигнала:
|
|
|
|
|
|
Спектр полученного сигнала выглядит следующим образом:
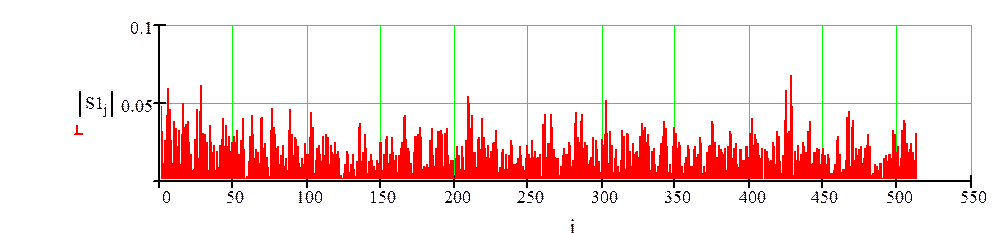
Рисунок 2.5–Спектр суммарного сигнала
Импульсная характеристика имеет следующий вид:
|
|
|
|
|
|
|
|
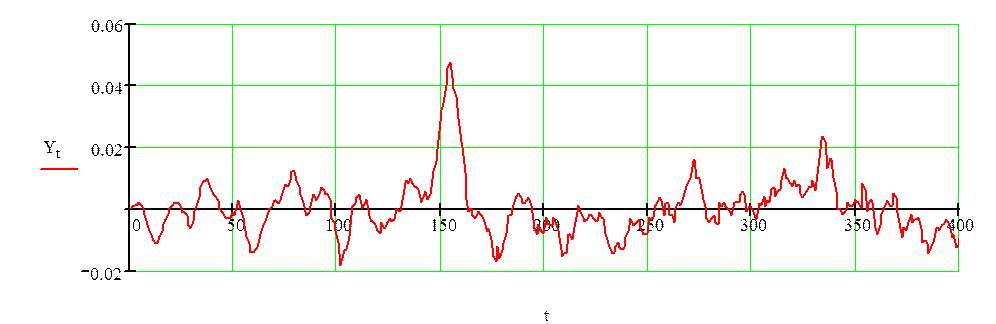
Рисунок 2.6–Сигнал на выходе, получаемый с помощью ОПФ
Составим программу для получения импульсной характеристики:
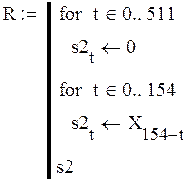
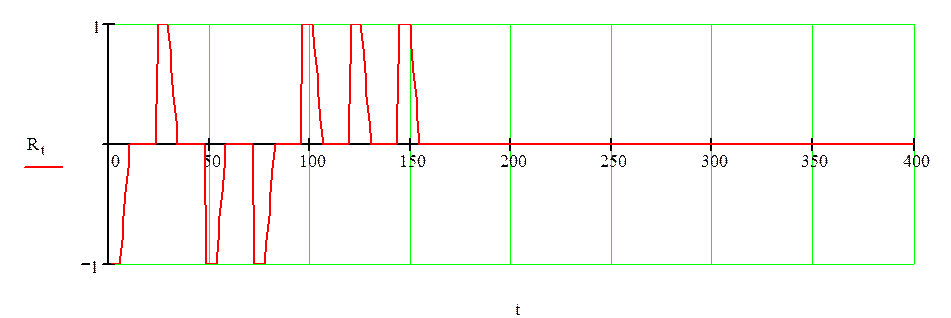
Рисунок 2.7–Импульсная характеристика
Напишем программу для получения выходной реализации с помощью свертки:
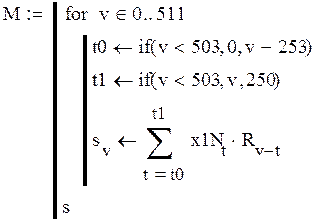
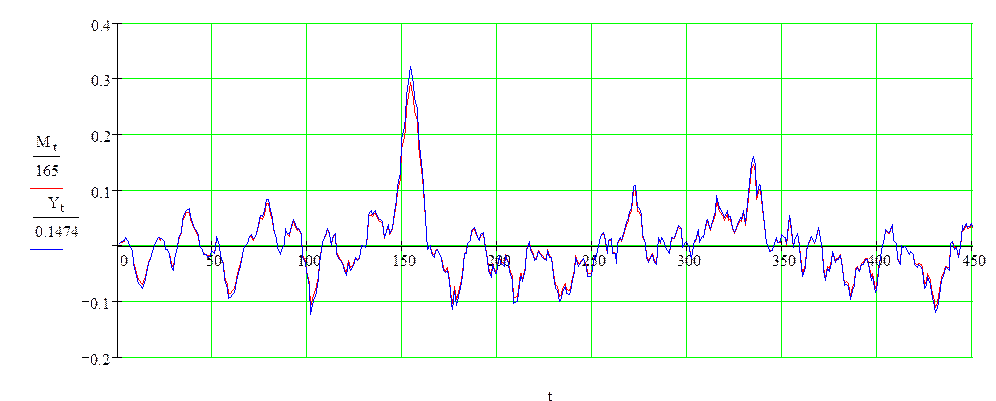
Рисунок 2.8 –Графическое сравнение результатов преобразования Фурье со сверткой зашумленного сигнала
Лабораторная работа №3
Определение статистических характеристик порогового приемника
Составим программу для получения выходного сигнала без шума с помощью свертки:
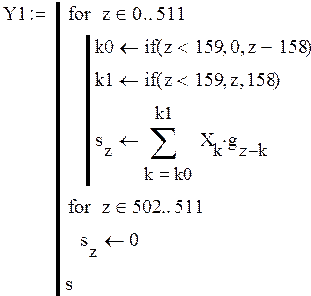
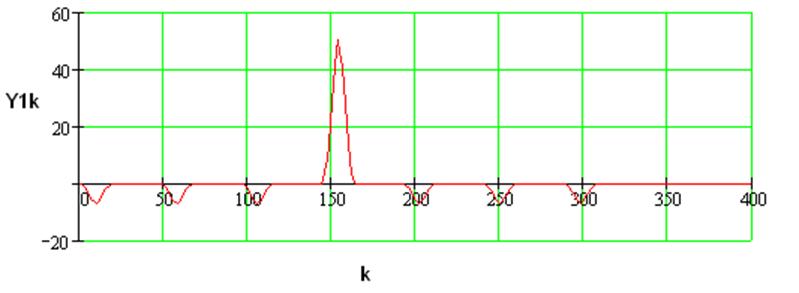
Рисунок 3.1–Выходной сигнал без шума
Определим максимальное значение выходного не зашумленного сигнала:
![]()
Зададимся следующими параметрами:
- Количество проводимых испытаний при одном значении порога
![]()
- Количество значений изменяемого порога
![]()
- Длительность сигнала (определяемое количеством выборок)
![]()
- Минимальное относительное значение порога
![]() .
.
Сформируем Гауссовский центрированный шум:
![]()
Составим программу для определения вероятности правильного обнаружения:
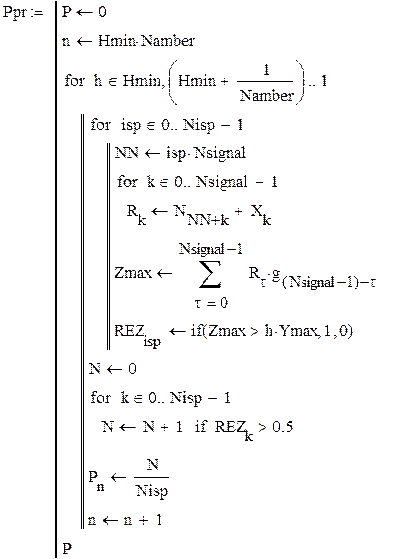
Вероятность пропуска сигнала:
![]()
Составим программу для определения вероятности ложной тревоги:
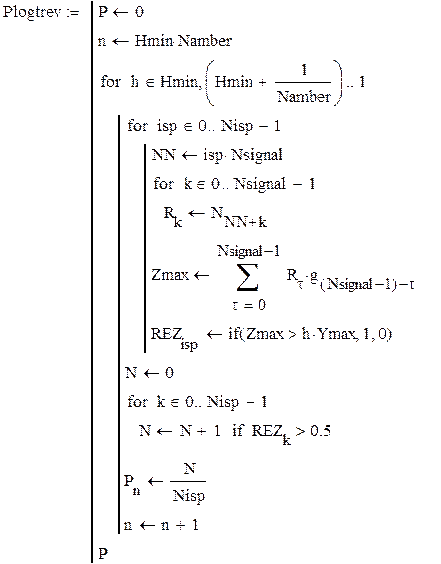
Вероятность правильного необнаружения:
![]()
Относительный порог:
![]()
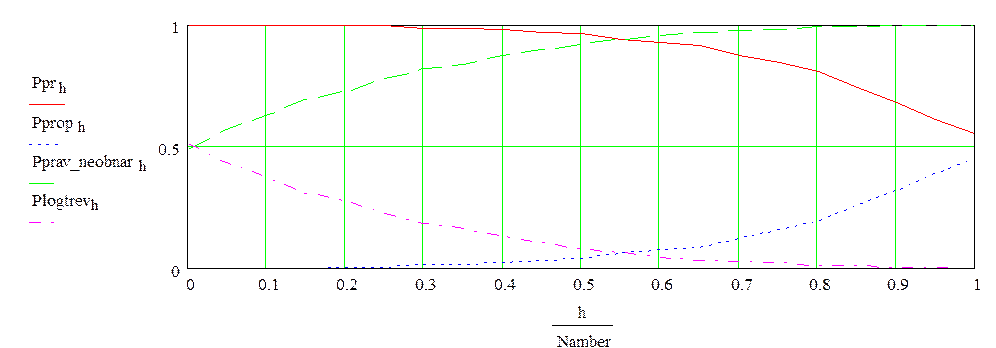
Рисунок 3.2–Вероятностные характеристики порогового приемника
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.