База сложных сигналов всегда много больше единицы. К таким сигналам относятся радиоимпульсы с модуляцией частоты заполнения. Наибольшее распространение получили линейная частотная модуляция (ЛЧМ) и фазовая манипуляция частоты заполнения. Использование сложных сигналов позволяет, значительно расширить дальность действия РЛС без увеличения энергетических показателей. С другой стороны, применение широкополосных сигналов позволяет повысить разрешающую способность по дальности и улучшить эффективность работы РЛС в условиях некоторых помех.
Обнаружение эхо-сигнала, отраженного от цели, состоит в принятии решения о наличии или отсутствии цели с минимальной вероятностью ошибки. Оптимальным обнаружителем является устройство, обеспечивающее наилучшее выделение сигнала из смеси сигнал + шум. Под шумом понимается стационарный случайный процесс с равномерной спектральной плотностью и нормальным распределением вероятностей возможных значений. В настоящее время хорошо разработаны и широко применяются следующие критерии оптимального обнаружения [3]:
· минимума среднего риска;
· минимальной "взвешенной" вероятности ошибки;
· минимума вероятности полной ошибки;
· Неймана-Пирсона.
Сущностью этих критериев является вычисление отношения правдоподобия и сравнение его с наперед заданным порогом.
Отношением правдоподобия называется величина
,
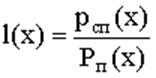где х - реализация принятой смеси сигнал + шум; Рсп(х) и Рп(х) - соответственно, вероятности, появления при условии наличия и отсутствия сигнала. Индекс “П” обозначает, что принимается только помеха, индекс “СП” - сигнал и помеха. На рис. П1 приведены графики условных плотностей вероятности Рсп(х) и Рп(х).
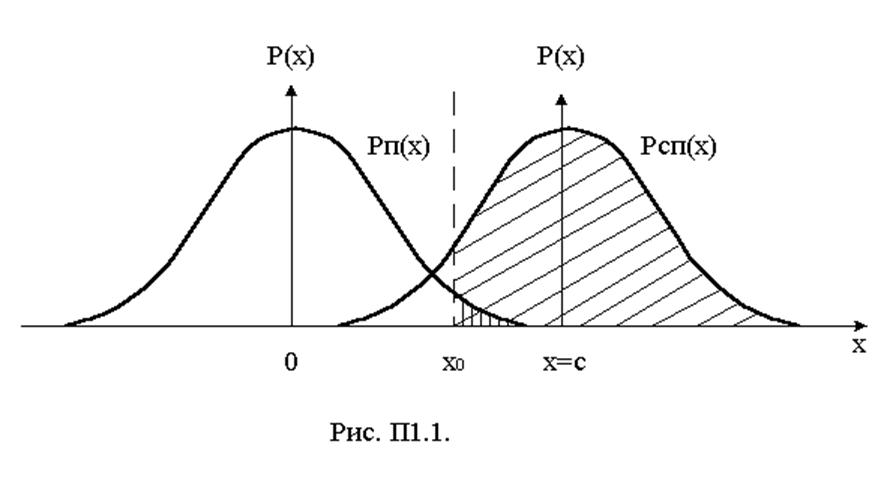
Превышение принимаемой реализацией порога считается фактом присутствия сигнала в смеси. Заштрихованная часть графика рис. П1.1 соответствует области принятия решения о том, что сигнал есть. Как видно, такое решение может быть принято (с достаточно малой вероятностью), когда принимается одна помеха (участок с двойной штриховкой), а принимается решение о наличии сигнала. Наперед задаваемым порогом здесь является X0.
Корреляционная теория оптимального обнаружения, основанная на определении отношения правдоподобия, реализуется устройствами, вычисляющими корреляционный интеграл вида
,
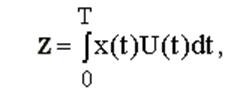где Х(t) – пр
инятая смесь сигнала с помехой; U(t)-опорное напряжение, т.е. "копия" сигнала.
В простейшем случае обнаружения сигнала с полностью известными параметрами такой коррелятор содержит перемножитель, интегратор и пороговое устройство. В [3 §2.4-2.8] подробно рассмотрено построение корреляторов для различных сигналов (со случайной начальной фазой, в виде пачки радиоимпульсов и т.д.). В любом варианте для работы коррелятора необходима копия сигнала, что создает дополнительные трудности, поскольку точное значение частоты и др. параметров сигнала на приемном конце может быть неизвестно. Кроме того, корреляционные измерители отличаются аппаратурной громоздкостью. Это объясняется тем, что для просмотра всей дальности (обнаружение целей на одном азимуте при различных удалениях) корреляторы должны быть многоканальными.
Задача оптимального обнаружения решается также с помощью согласованной фильтрации, причем при работе согласованного фильтра (СФ) копия сигнала не нужна. Для сигнала Uc(t) согласованным является фильтр с передаточной характеристикой, которая является комплексно-сопряженной со спектром принимаемого сигнала (с точностью до постоянного множителя и задержки во времени, вносимой фильтром). Если спектр сигнала
,
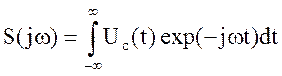то передаточная характеристика (комплексный коэффициент передачи)
.
Здесь k - - постоянный
множитель; 
- член, характеризующий постоянную
временную задержку сигнала в фильтре, 
-
функция, комплексно сопряженная спектру сигнала.
Отклик согласованного фильтра аналогичен отклику коррелятора. Поэтому применение СФ во многих случаях позволяет решить задачу обнаружения более эффективно и технически менее громоздко. Например, СФ для одиночного радиоимпульса с прямоугольной огибающей (без внутриимпульсной модуляции) состоит из арифметического устройства, которое вырабатывает разность задержанного и незадержанного импульсов и колебательный контур высокой добротности (рис. П1.2).
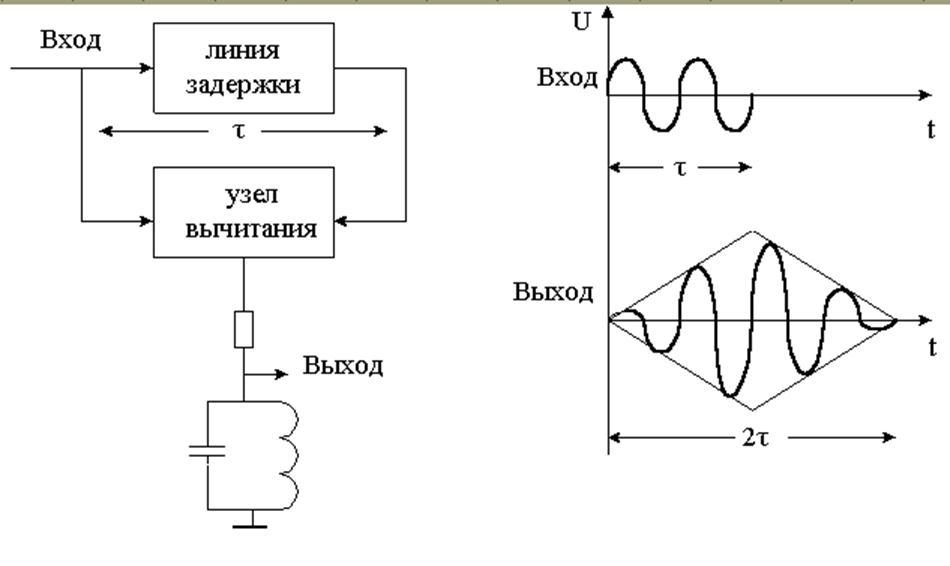
Рис. П1.2
На контуре высокой добротности происходит нарастание амплитуды напряжения в течение длительности импульса и медленный спад после его окончания. В результате вычитания двух переходных процессов и получается ромбовидный радиоимпульс. В [3, § 2.9-2.11] подробно рассмотрено построение СФ различных сигналов.
Весьма эффективным является использование согласованной фильтрации широкополосных сигналов. Проблема расширения дальности действия РЛС может быть решена увеличением энергии сигнала, что обеспечивается повышением выходной мощности передатчика. Однако такой метод на практике не применяется, поскольку лампы выходных каскадов и фидерные тракты имеют ограниченный запас электрической прочности. Другой способ состоит в увеличении длительности излучаемых импульсов, что резко снижает разрешающую способность по дальности, использование согласованной фильтрации широкополосных сигналов обеспечивает возможность разрешать сигналы от целей, ответные импульсы от которых даже перекрываются.
Рассмотрим принцип сжатия двух широкополосных сигналов с внутриимпульсной линейной модуляцией (ЛЧМ) и фазо-манипулированных импульсов (сигналы с ФМ).
Сигналы с ЛЧМ
Сигнал с ЛЧМ представляет собой радиоимпульс, частота которого линейно изменяется (увеличивается или уменьшается) от начала к концу импульса. Фильтр, оптимальный для ЛЧМ-радиоимпульса должен иметь импульсную характеристику в виде ЛЧМ-импульса, зеркально отображенного относительно сигнала. Если у исходного радиоимпульса сгущения были справа, а разрежения – слева (левый график на рис. П1.3),
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.