Эти законы приведены с целью проводить стохастические расчеты в решении поставленных задач.
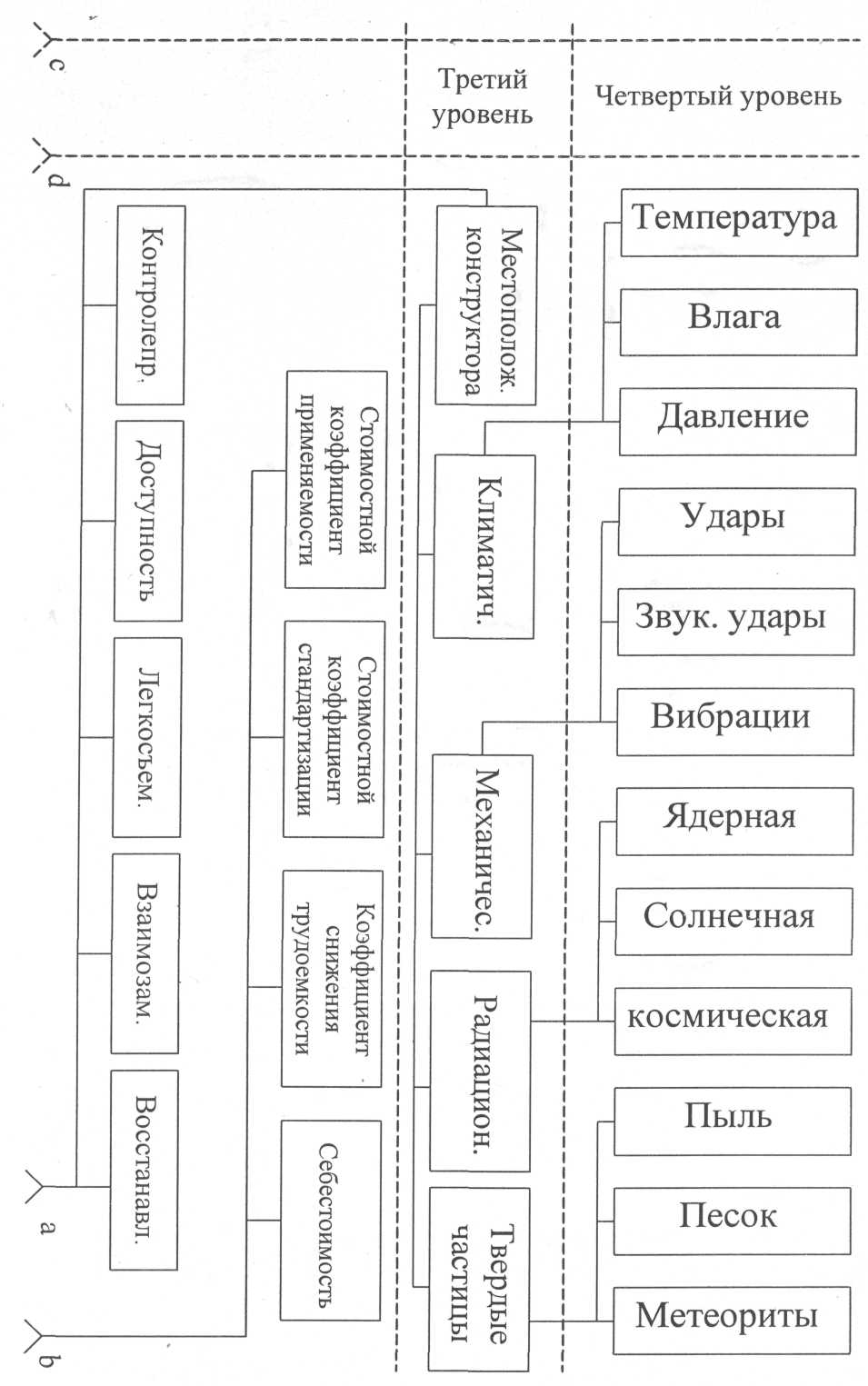
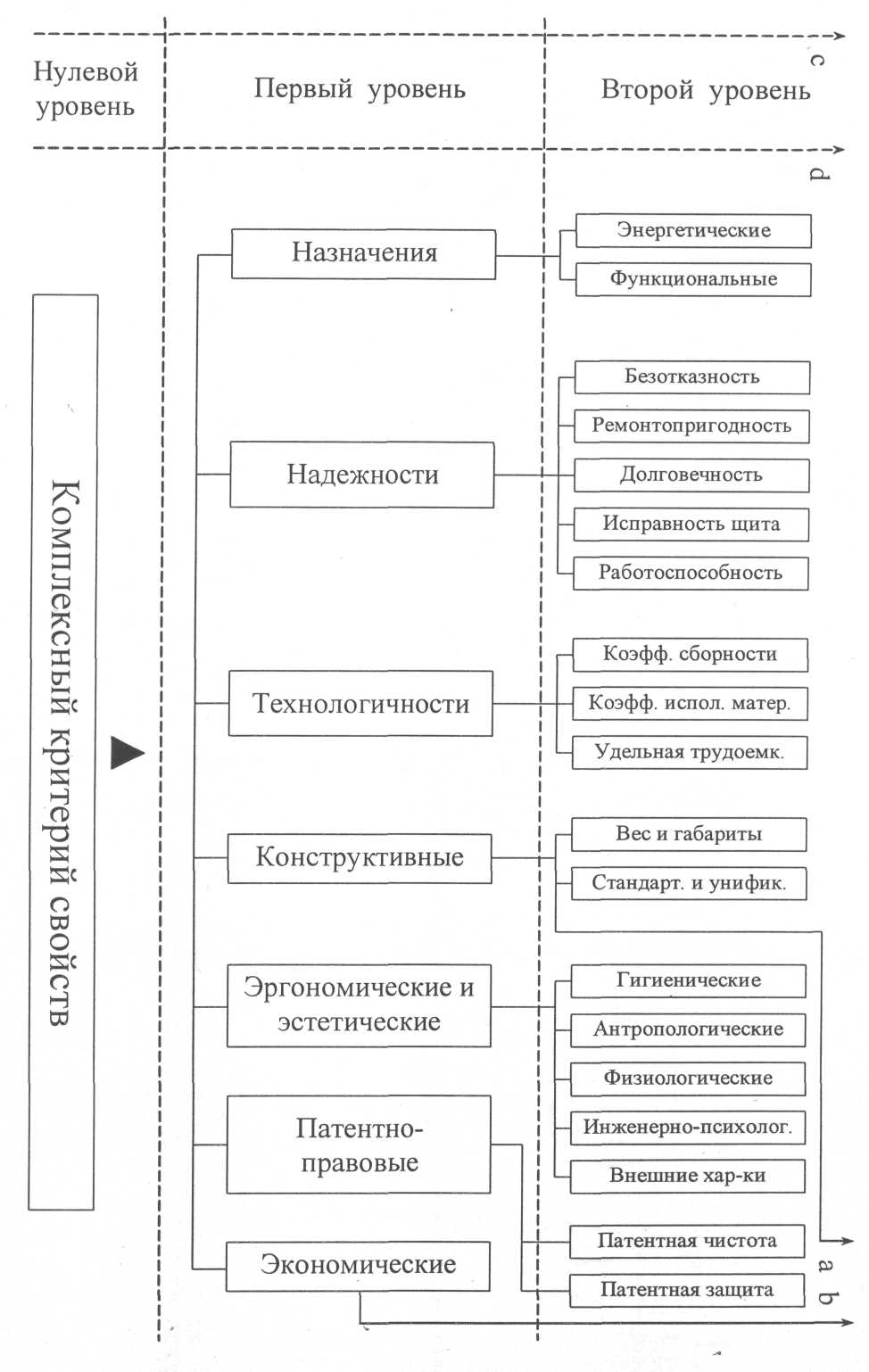
В реальных условиях законы распределения параметров часто оказываются неизвестными. В таких случаях для уменьшения ошибок решения задач можно использовать закон равной вероятности или нормальный закон распределения случайных величин.
Порождение нормального закона распределения параметра от композиции ряда его состояний можно показать на основе стохастического моделирования. При этом в качестве непрерывной модели состояний берется распределение случайных величин по закону равнобедренного треугольника (рис.2.7).
Если оценки состояний параметра f(Sj) представляются случайными величинами, то результаты моделирования также можно отнести к плотностям распределения параметра f(Xj), рис.2.7. Сам процесс моделирования основывается на генераторе случайных чисел и специальном подходе к их обработке. Результаты моделирования позволяют выявить следующие частные свойства плотностей распределения параметра (рис.2.7).
1. Композиция ряда состояний плотностей, распределенных по нормальному закону, в целом приводит к закону близкому к нормальному.
2. Часть плотности распределения параметров выходит за левую и правую границу поля допуска и в формировании плотности f(S) не участвует.
3.
У
кривой нормального распределения отсекаются те ее части, для
которых
плотности f(xj) выходят за границы поля допуска.
4. Плотность распределения параметра плотности f(x) размещается внутри поля допуска:
^-справа хы <[М*(хо)-За*, M*(xo) + 3a)<x2i
(2.22) <- слева хи <{м*{хо)-Ъ(т\ М*(хо) + 3а*х)<хы
Относительно номинального значения параметра
где М*(х0),3о*х - соответственно оценки математического ожидания и среднеквадратического отклонения параметра.
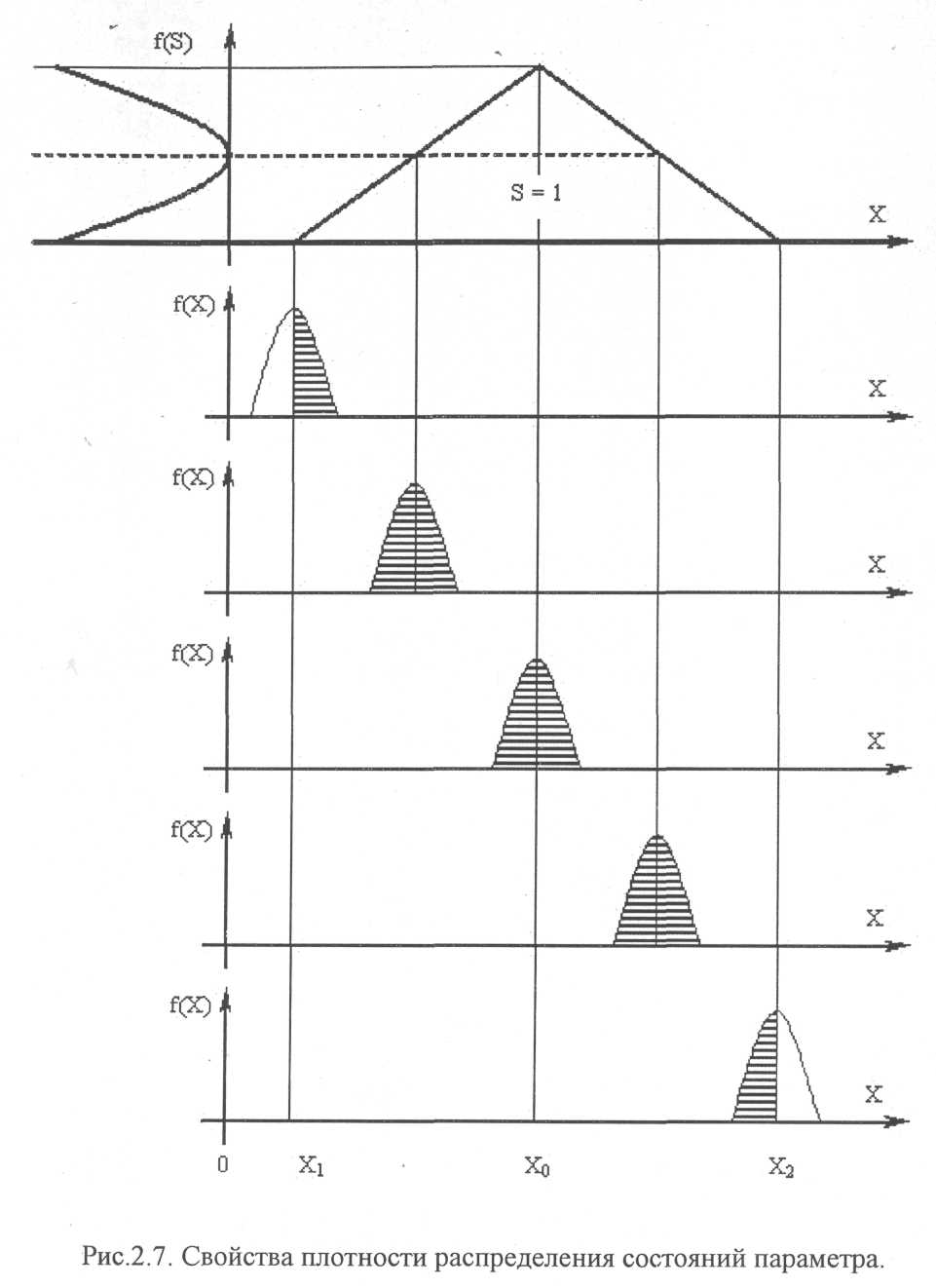
Законы распределения параметров в пределах установленных допусков встречаются самые разнообразные. Некоторые из них могут быть апроксимированны широко известными видами законов. Знание законов распределения параметров ЭС в значительной степени облегчает процесс их
разработки – уменьшает вероятность ошибок установленных норм на всех этапах и стадиях создания ЭС, сокращает время разработки за счет исключения процессов доработок и доводок.
Большое отличие от технических норм бывает у таких параметров устройств, контроль которых в производственных условиях затруднен. Например, величины интенсивности отказов многих устройств, даже одного и того же назначения имеет большой разброс. Иногда он достигает до двух и даже более порядков.
2.1.8. Общие понятия о допусках параметров ЭС
Известно, что требуемое качество и надежность ЭС обеспечивается высокой точностью их функционирования. При этом высокая точность работы аппаратуры обеспечивается подбором допусков на входные, промежуточные и выходные ее параметры, а также на параметры смежных и конструктивных элементов.
Заметим, что номинальные значения параметров определяются, как правило, разработчиками известными методами инженерных расчетов. Выше отмечалось, что отклонения параметров от номинальных значений носят случайный характер со случайными сочетаниями их погрешностей. Очевидно, что расчет допусков ЭС следует проводить, пользуясь правилами теории вероятностей. В этом случае одних числовых характеристик законов распределения случайных величин совершенно не достаточно для расчета допусков. Поэтому при их расчете по вероятностному методу необходимо пользоваться числовыми характеристиками законов распределения, связанными через определенные соотношения с характеристиками поля допуска. Совместно эти характеристики дают наиболее полную картину распределения отклонений параметров от их номинальных значений в пределах поля допуска. На рис.2.8 они показаны в относительных погрешностях
параметров. Где 5 — - половина поля допуска, Е\— - координата ее
VX ) \ X )
середины поля допуска, М\ — - математическое ожидание распределения
vXJ
отклонения (центр группирования случайной величины), а - коэффициент асимметрии.
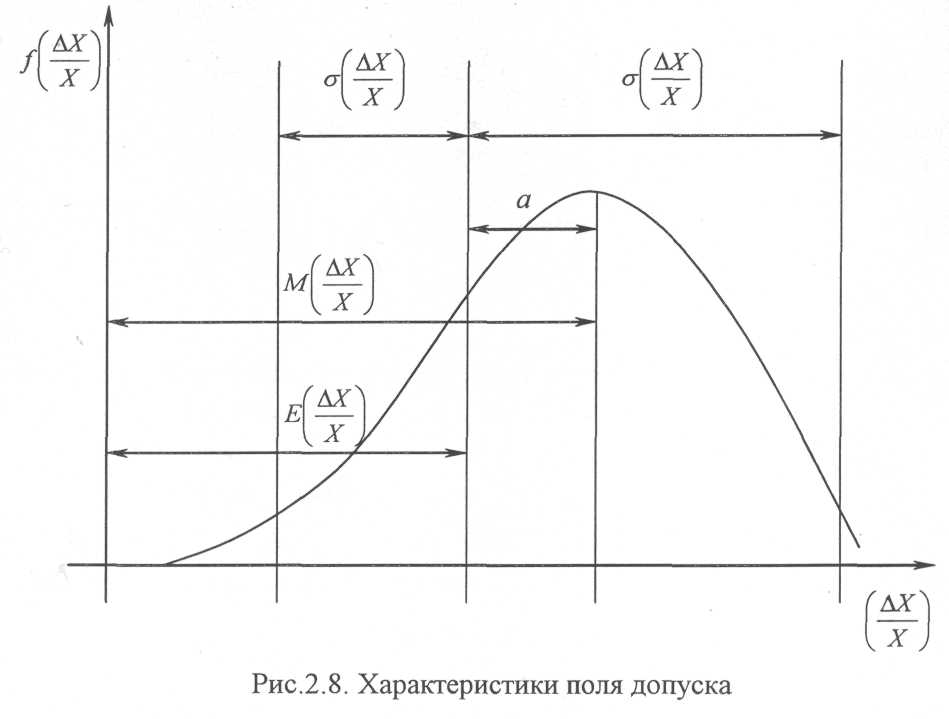 Учитывая
сказанное, нетрудно дать некоторые понятия о допусках параметров.
Учитывая
сказанное, нетрудно дать некоторые понятия о допусках параметров.
Допуски – граничные значения соответствующих параметров, внутри которых устройство выполняет функции, предназначенные для него.
Их можно классифицировать следующим образом.
По характеру:
механические – граничные значения параметров, устанавливаемые от механических погрешностей;
электрические – граничные значения параметров, устанавливаемые от электрических погрешностей.
По назначению:
производственные – ограничение поля рассеивания параметров, вызванное производственными погрешностями;
эксплуатационные – ограничение поля рассеивания параметров, вызванное эксплуатационными погрешностями;
ремонтные – ограничение поля рассеивания параметров, вызванное ремонтными погрешностями.
По местоположению:
двухсторонние – ограничение поля рассеивания параметров, установленное с двух их сторон;
одностороннее – ограничение поля рассеивания параметров, установленное с одной их стороны.
Двухсторонние допуски, это наиболее распространенная их группа. Однако у ряда устройств имеются параметры, для которых не имеет практического значения одна из границ допусков. Например, вероятность безотказной работы аппаратуру и др.
Подчеркнем, что только при правильном обеспечении рассмотренных допусков на параметры могут быть получены требуемые показатели ЭС, без него невозможна автоматизация производства аппаратуры. При этом процесс расчета и отработки допусков аппаратуры должен проводиться на всех этапах и стадиях жизненного ее цикла. Наиболее правильно было бы обеспечивать допуски аппаратуры, начиная с ее выходных параметров и заканчивая установлением допусков на ее элементы. Следует помнить, что выход хотя бы одного параметра за поле установленного допуска, считается отказом всего устройства.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.