Очевидно, что привлечение большого количества сечений в реализациях (рис.1) приведет к более полной информации о случайном процессе. Полной характеристикой процесса являются функции (2.5, 2.6) в многомерном пространстве данного параметра:
Интегральная функция
![]() (2.8)
(2.8)
Дифференциальное уравнение
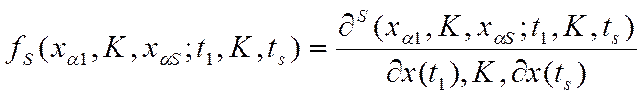 (2. 9)
(2. 9)
Значит интегральная и дифференциальная функции полностью характеризуют стохастические свойства случайного процесса параметров ЭС при их разработке.
2.1.7 Вероятностные функции состояний параметров ЭС
При решении задач оценки и управления ПЭ ЭС важно знать законы распределения параметров на этапах и стадиях их разработки. В
литературе обширно и глубоко рассматриваются различные законы распределения случайных величин.
Известно, что к случайным величинам относятся как значения параметров, так и величины их допусков [ ]. Однако отсутствуют конкретные рекомендации о соответствующем законе распределения того или иного параметра ЭС.
Заметим,
что в пределах заданного допуска величины параметра распределяются случайным
образом, то соответствие его распределения конкретному
закону должно проводится по правилам теории вероятностей. На рис.2.3
показано равномерное распределение плотности вероятности параметра ![]() .
.

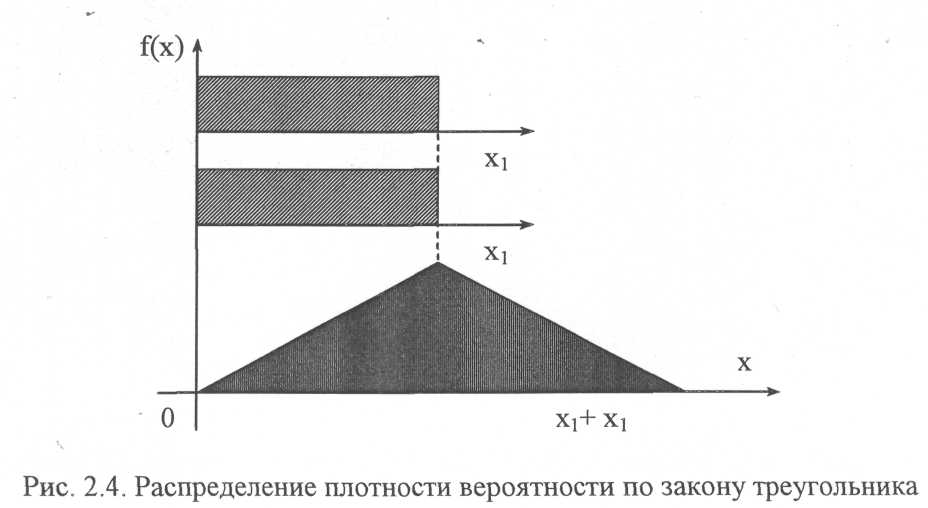
Пусть имеется композиция двух параметров с равномерным их распределением. В результате суммирования двух случайных величин данного распределения с одинаковыми областями рассеивания получаем закон распределения равнобедренного треугольника (рис.2.4).
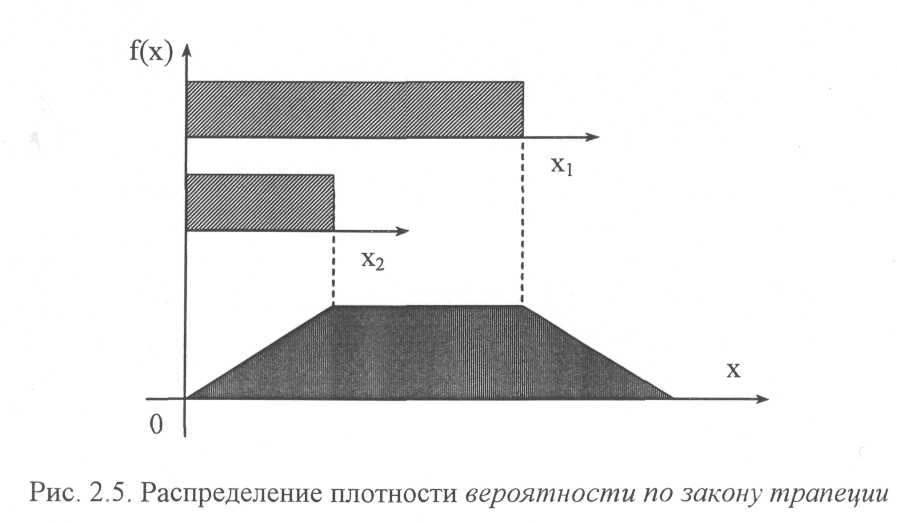
Если же области рассеивания двух случайных величин различны при равномерном законе их распределения, то суммирование их приводит к трапециидальной форме закона. При этом, чем больше разность областей рассеивания, тем длиннее верхняя линия трапеции (рис.2.5).
 Характерно,
что композиция двух случайных величин, подчиняющихся закону равнобедренного
треугольника, соответствует нормальному закону (рис.2.6).
Характерно,
что композиция двух случайных величин, подчиняющихся закону равнобедренного
треугольника, соответствует нормальному закону (рис.2.6).
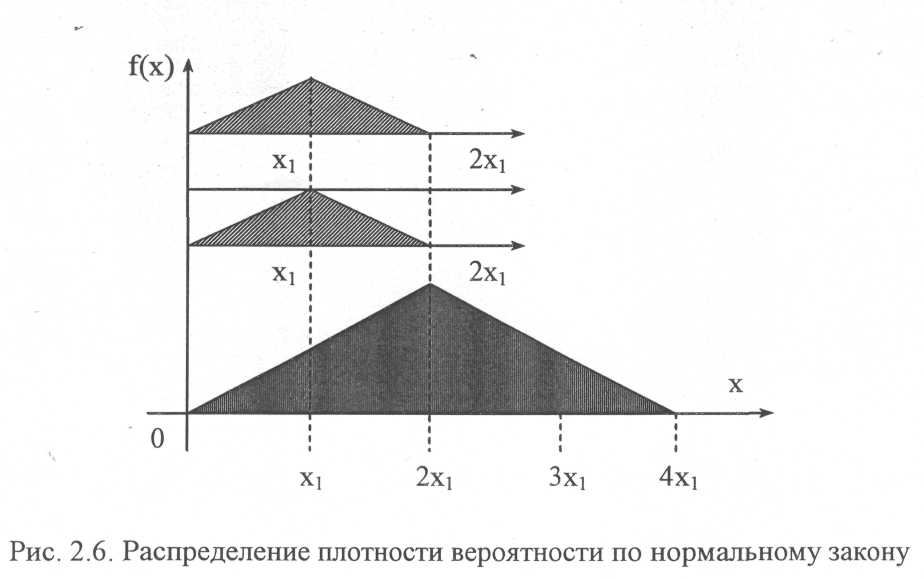
Очевидно, что сумма четырех случайных величин с равновероятностным распределением и одинаковыми областями рассеивания аккумулирует распределение, близкое к нормальному. Это важное обстоятельство для практики свидетельствует о том, что нормальным законом аппроксимируется распределение выходного параметра устройства, если он зависит от определенного числа параметров, хотя бы более четырех. Если выходной параметр устройства описывается двумя или тремя показателями, случайная величина каждого из которых имеет распределение отличное от нормального, то аппроксимацией пользоваться крайне некорректно. Этим обстоятельством и объясняется то, что практически большинство выходных параметров устройств подчиняются закону нормального распределения. Выходные параметры устройств имеют некоторые средние величины и определенные их разбросы, которые регламентируются определенными отклонениями –допусками. Характерно, что разброс параметров устройств в сложных эксплуатационных условиях может оказаться значительно больше, чем указываемые в ТЗ.
Очередным обоснованием возможности использования нормального закона распределения значений параметра при разработке ЭС является следующий важный аспект. На величины соответствующего параметра в процессе достижения его соответствующего уровня качества влияет множество факторов, в том числе такие как:
· неточности технологических режимов;
· погрешности технологической оснастки;
· ошибки на уровне человеческих факторов;
· необходимость учета реальных условий эксплуатации ЭС, т. е.
влияние как внешних, так и внутренних дестабилизирующих факторов и т. д.
В целом это соприкасается с центральной предельной теоремой вероятности, как множество факторов, влияющих на величину соответствующего параметра в процессе производства ЭС.
Очевидно, что изменение параметра в пределах его граничных значений будет подчиняться ближе всего к закону нормального распределения.
С практических позиций для решения поставленных задач наибольший интерес представляют такие законы распределения случайных величин как равномерный, треугольный и нормальный.
Для равномерного закона распределения справедливы следующие количественные характеристики [ ]:
Среднее значение параметра
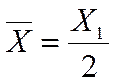 (2.10)
(2.10)
Плотность распределения вероятности
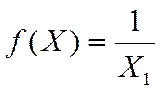 (2.11)
(2.11)
Дисперсия распределения параметра
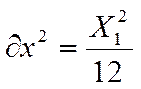 (2.12)
(2.12)
Для распределения по закону равнобедренного треугольника имеем [ ]:
Среднее значение параметра
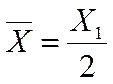 (2.13)
(2.13)
Плотность
вероятности для области 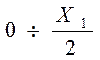
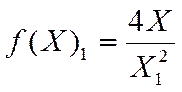 (2.14)
(2.14)
для области
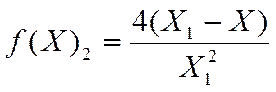 (2.15)
(2.15)
Дисперсия распределения параметра
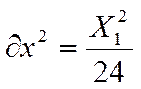 (2.16)
(2.16)
Для нормального закона распределения характерно: среднее значение в начале отсчета, совпадающим с центром группирования равно
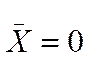
плотность вероятности записывается так
![]() /(*)= * е ^2
/(*)= * е ^2
5 л/Л
х
А функция распределения, как вероятность того, что случайная величина лежит в соответствующих пределах, равна
![]() P{a<x<b) = -^]e25*2с1х(2Л8)
P{a<x<b) = -^]e25*2с1х(2Л8)
л:
Пользоваться приведенными формулами гораздо удобнее, если вводится нормированная величина
х
Z=T
х. Тогда функция распределения имеет вид
F{x)=-^JT^dz(2-19)
V2I1 -со
Интеграл (2.19) не выражается элементарными функциями. Поэтому для вычисления искомых интегралов водится табулированная функция
_^
O(*)=-*=Je 2dz (2.20)
л/2По
При законе нормального распределения область возможных значений случайной величины находится в пределах ±оо. Однако в практике принято считать предельным отклонением
Ах = ±3их « бих
![]()
![]() 6 ■* 36
6 ■* 36
Характерно, что для рассмотренных законов распределения случайных величин, площадь, заключенная между линиями и осью абсцисс, равна единице.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.