









11. КИНЕМАТИЧЕСКИЕ И СИЛОВЫЕ
ХАРАКТЕРИСТИКИ
ПЛАНЕТАРНого РЕДУКТОРа
(лабораторная работа № 11)
Цель работы: изучить кинематическую схему и конструкцию планетарного редуктора, определить его кинематические параметры и КПД при различных режимах работы.
Краткие теоретические сведения
Механизмы зубчатых передач с подвижными осями
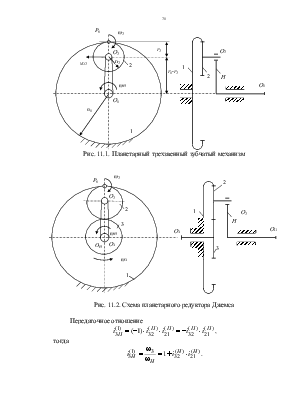
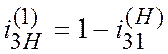
В трехзвенном зубчатом механизме (рис. 11.1)
зубчатое колесо 1 неподвижно, зубчатое колесо 2 имеет подвижную ось О2.
Звено Н входит во вращательные пары О1 со стойкой О2
с зубчатым колесом 2. При вращении звена Н с угловой скоростью ![]() колесо 2 обегает неподвижное колесо
1, вращаясь с угловой скоростью
колесо 2 обегает неподвижное колесо
1, вращаясь с угловой скоростью ![]() вокруг
мгновенного центра вращения Р0. Колесо 1 называется
центральным колесом, колесо 2 — сателлитом, звено Н — водилом. Связь
между угловыми скоростями
вокруг
мгновенного центра вращения Р0. Колесо 1 называется
центральным колесом, колесо 2 — сателлитом, звено Н — водилом. Связь
между угловыми скоростями ![]() и
и ![]() устанавливается следующим образом:
для скорости
устанавливается следующим образом:
для скорости ![]() точки О2,
являющейся общей для колеса 2 и водила Н, имеем:
точки О2,
являющейся общей для колеса 2 и водила Н, имеем:
![]() . (11.1)
. (11.1)
Следовательно, передаточное отношение
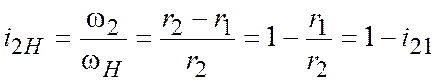 . (11.2)
. (11.2)
Из этих равенств видно, что ![]() — есть передаточное отношение при
неподвижном колесе 1, а
— есть передаточное отношение при
неподвижном колесе 1, а ![]() — передаточное
отношение трехзвенного зубчатого механизма с колесами, имеющими неподвижные
оси, т.е. при неподвижном водиле Н. В дальнейшем, чтобы знать, у какого
неподвижного звена определять то или иное передаточное отношение, будем в
скобках ставить индекс того звена которое неподвижно:
— передаточное
отношение трехзвенного зубчатого механизма с колесами, имеющими неподвижные
оси, т.е. при неподвижном водиле Н. В дальнейшем, чтобы знать, у какого
неподвижного звена определять то или иное передаточное отношение, будем в
скобках ставить индекс того звена которое неподвижно:
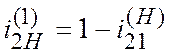 . (11.3)
. (11.3)
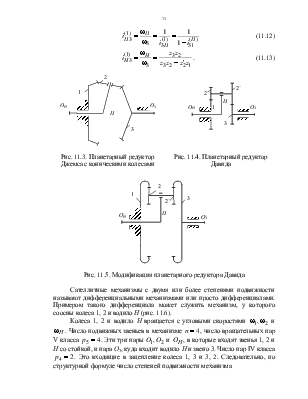
Простейший планетарный редуктор, состоящий из четырех звеньев, можно получить из планетарного механизма, если в него ввести еще одно зубчатое колесо 3 с осью О3, входящее в зацепление с сателлитом 2 (рис. 11.2).
Передаточное отношение ![]() от вала О3 к валу ОН
определяют по формуле
от вала О3 к валу ОН
определяют по формуле
 . (11.4)
. (11.4)
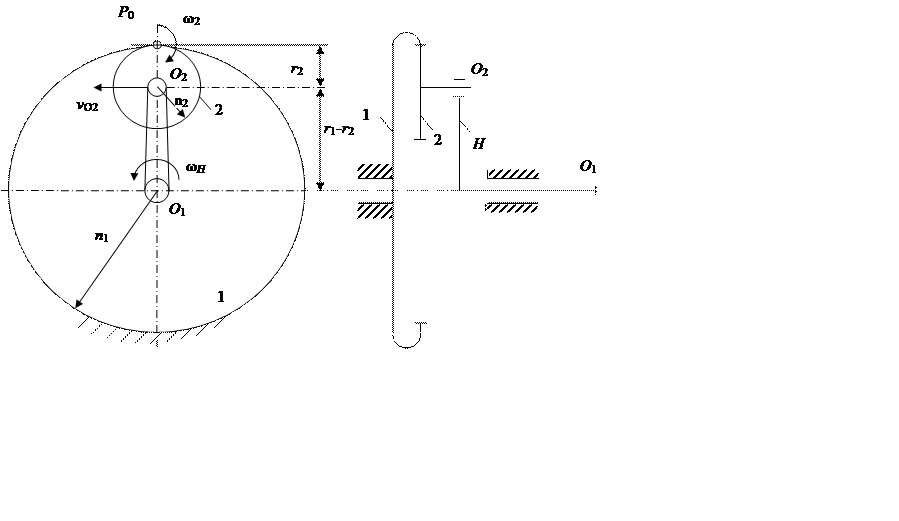 |
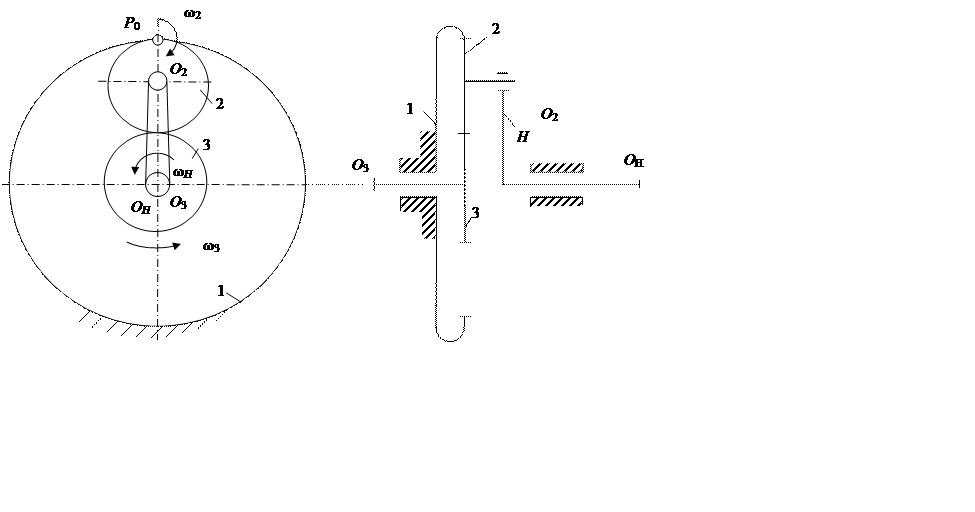
Рис. 11.2. Схема планетарного редуктора Джемса
Передаточное отношение
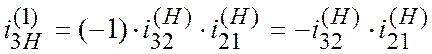 ,
,
тогда
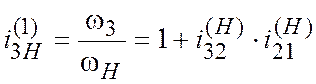 .
.
Если ввести в это уравнение радиусы
начальных окружностей ![]() или числа зубьев
или числа зубьев ![]() , то формула примет вид
, то формула примет вид
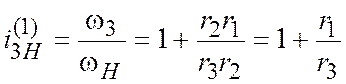 (11.5)
(11.5)
или
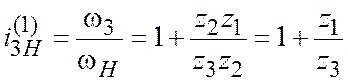 (11.6)
(11.6)
Передаточное отношение ![]() от водила Н к колесу 3 редуктора находят
из выражения
от водила Н к колесу 3 редуктора находят
из выражения
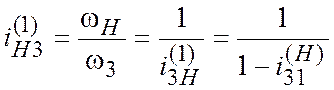 (11.7)
(11.7)
или
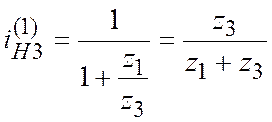 . (11.8)
. (11.8)
По-прежнему
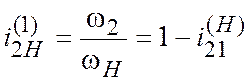 , (11.9)
, (11.9)
отсюда
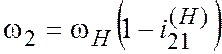 . (11.10)
. (11.10)
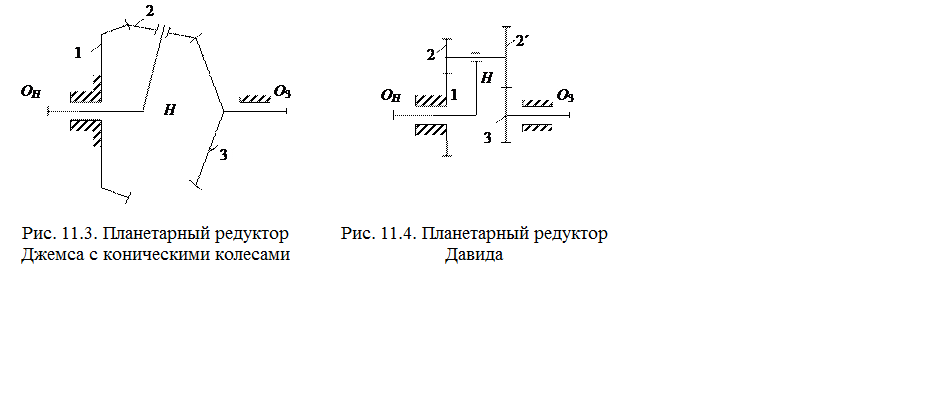
Рассмотренный нами планетарный редуктор называется редуктором Джемса (рис. 11.2). Планетарный редуктор такого типа можно составить также из круглых конических колес (рис. 11.3).
Передаточное отношение редуктора с коническими колесами (рис. 11.3) определяют по (11.5) — (11.8). Планетарный редуктор, выполненный по схеме, показанной на рис.2.4, называют редуктором Давида. Передаточное отношение от вала О3 к валу ОН находят по формуле
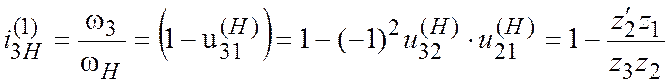 . (2.11)
. (2.11)
Из этого равенства следует, что если
подобрать числа зубьев ![]() колес 1, 2, 2´, 3
так, чтобы второй член в уравнении был близок к единице, то передаточное
отношение может быть весьма мало. Возможна модификация редуктора Давида (рис.
11.5) с сателлитом, входящим в два внутренних зацепления. Обычно в этой
модификации ведущим является водило Н, и передаточное отношение
колес 1, 2, 2´, 3
так, чтобы второй член в уравнении был близок к единице, то передаточное
отношение может быть весьма мало. Возможна модификация редуктора Давида (рис.
11.5) с сателлитом, входящим в два внутренних зацепления. Обычно в этой
модификации ведущим является водило Н, и передаточное отношение ![]() от вала ОН к валу О3
определяют по формуле
от вала ОН к валу О3
определяют по формуле
 (11.12)
(11.12)
 |
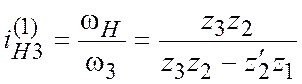 . (11.13)
. (11.13)
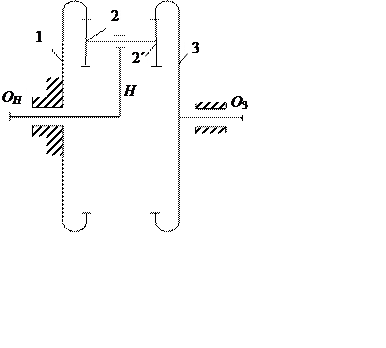
Рис. 11.5. Модификация планетарного редуктора Давида
Сателлитные механизмы с двумя или более степенями подвижности называют дифференциальными механизмами или просто дифференциалами. Примером такого дифференциала может служить механизм, у которого соосны колеса 1, 2 и водило Н (рис. 11.6).
Колеса 1, 2 и водило Н вращается с
угловыми скоростями ![]() и
и ![]() .
Число подвижных звеньев в механизме
.
Число подвижных звеньев в механизме ![]() , число
вращательных пар V класса
, число
вращательных пар V класса ![]() . Эти три пары
. Эти три пары ![]() и
и ![]() ,
в которые входят звенья 1, 2 и Н со стойкой, и пара О3,
куда входит водило Н и звено 3. Число пар IV класса
,
в которые входят звенья 1, 2 и Н со стойкой, и пара О3,
куда входит водило Н и звено 3. Число пар IV класса ![]() . Это входящие в зацепление колеса 1,
3 и 3, 2. Следовательно, по структурной формуле число степеней подвижности
механизма
. Это входящие в зацепление колеса 1,
3 и 3, 2. Следовательно, по структурной формуле число степеней подвижности
механизма
![]() . (11.14)
. (11.14)
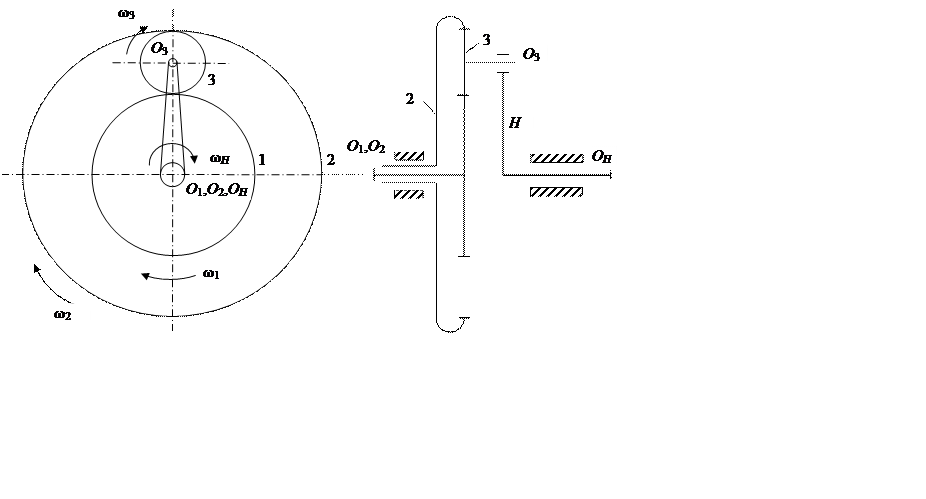
Рис. 11.6. Простейший дифференциальный механизм
Таким образом, для определенности
движения механизма необходимы законы движения двух звеньев. Выбор последних
может быть произвольным. Например, можно задаться законом движения звеньев 2 и Н,
т.е. законами изменения углов поворота ![]() и
и
![]() Н звеньев 2 и Н.
Тогда угол поворота звена 1
Н звеньев 2 и Н.
Тогда угол поворота звена 1
![]() .
.
По правилу дифференцирования сложных функций с несколькими переменными получаем
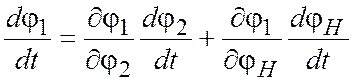 ,
,
где
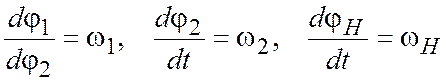 .
.
Из вышеописанного получим
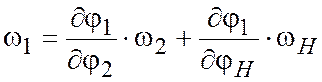 . (11.15)
. (11.15)
Уравнение (11.15) связывает угловые скорости звеньев
1, 2 и Н. Угловая скорость ![]() колеса 3 не
входит в это уравнение, так как колесо 3 является паразитным (паразитным
называется зубчатое колесо, которое не влияет на величину передаточного отношения
механизма). Частные производные от угла
колеса 3 не
входит в это уравнение, так как колесо 3 является паразитным (паразитным
называется зубчатое колесо, которое не влияет на величину передаточного отношения
механизма). Частные производные от угла ![]() по
углам
по
углам ![]() и
и ![]() (см.
формулу 11.15) являются соответствующими передаточными отношениями при
неподвижных звеньях 2 и Н:
(см.
формулу 11.15) являются соответствующими передаточными отношениями при
неподвижных звеньях 2 и Н:
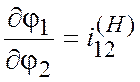 ,
, 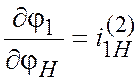 .
.
Теперь уравнение (11.15), связывающее угловые скорости звеньев 1, 2 и Н можно переписать в виде
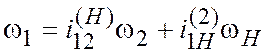 .
.
Передаточное отношение представляют в виде
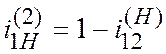 .
.
Тогда
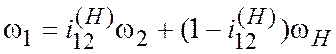 .
.
После преобразования 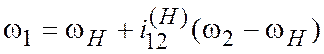 или
или
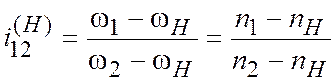 , (2.16)
, (2.16)
где ![]() и
и ![]() — соответственно количество оборотов
в минуту звеньев 1, 2 и Н.
— соответственно количество оборотов
в минуту звеньев 1, 2 и Н.
Эта формула является формулой Виллиса для дифференциалов.
Коэффициент полезного действия
В планетарных передачах КПД зависит от величины потерь во всех зацеплениях, а также от величины и знака передаточного отношения. Значение коэффициента потерь в каждом из зацеплений планетарного редуктора рассчитывают по формуле
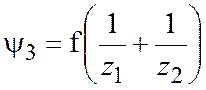 , (11.17)
, (11.17)
где ![]() и
и ![]() — числа зубьев первого и второго
зубчатых колес;
— числа зубьев первого и второго
зубчатых колес; ![]() — коэффициент трения в
зубчатом зацеплении.
— коэффициент трения в
зубчатом зацеплении.
При консистентной смазке для открытых
зубчатых передах ![]() = 0,1…0,16. В формуле
(11.17) знак (+) означает внешнее зацепление, (+) — внутреннее.
= 0,1…0,16. В формуле
(11.17) знак (+) означает внешнее зацепление, (+) — внутреннее.
Полный коэффициент потерь во всех зацеплениях передачи
![]() . (11.18)
. (11.18)
КПД исследуемой планетарной передачи рассчитывают по формуле
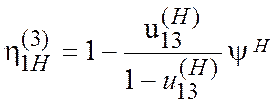 . (11.19)
. (11.19)
Практическая часть
Приборы и принадлежности: прибор типа ДП5А для изучения работы планетарного редуктора, секундомер.
Устройство и работа установки
Прибор ДП5А, изображен на рис. 11.7. Все узлы смонтированы на литом основании 16, внутри которого расположены блоки управления прибором.

Узел электродвигателя смонтирован на литом кронштейне 17. Статор электродвигателя 3 установлен в двух шарикоподшипниковых спорах 2 и 6 (балансирный электродвигатель). Ротор электродвигателя упругой муфтой 7 соединяют с входным валом редуктора.
К левой стороне кронштейна 17 закреплен цилиндрический корпус 1, в котором установлен тахометр, измеряющий частоту вращения ротора электродвигателя.
В передней части кронштейна смонтировано измерительное устройство, состоящее из тензоболочки 5, индикатора 4 и державки индикатора. Этим устройством воспринимается и измеряется реактивный момент электродвигателя.
Испытуемый планетарный редуктор 9 представлен
шестью зубчатыми колесами (рис. 11.8). Ведущее зубчатое колесо (![]() ) вращается вокруг своей оси, а
центральное колесо 3 (
) вращается вокруг своей оси, а
центральное колесо 3 (![]() ) жестко связано с корпусом
редуктора. Водило Н с двумя парами сателлитов (
) жестко связано с корпусом
редуктора. Водило Н с двумя парами сателлитов (![]() )
и (
)
и (![]() ), находящимися в зацеплении с
центральными колесами, выполнено совместно с валиком, который муфтой 10
соединен с нагрузочным устройством.
), находящимися в зацеплении с
центральными колесами, выполнено совместно с валиком, который муфтой 10
соединен с нагрузочным устройством.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.