Возможно также вычисление ДПФ по числу точек N < N1 (N = N1/2, N = N1/3 и т. д., т. е. с прореживанием спектра).
Число усредняемых окон (секций) сигнала L, большее
1, используется при гармоническом анализе (режим СПЕКТР) для повышения точности
оценки параметров зашумленных сигналов. При этом ДПФ вычисляется для
усредненной по L секциям реализации сигнала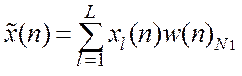 
.
Увеличить число усредняемых окон (секций) при заданном времени анализа можно
путем их перекрытия во времени с заданным коэффициентом перекрытия окон.
Отсутствию перекрытия соответствует коэффициент перекрытия, равный 1.
Начало первого окна анализа Nн, отличное от нуля, устанавливается при спектральном анализе выходных сигналов цифровых фильтров и выбирается не менее длины их импульсной характеристики.
Анализ энергетических спектров сигналов – спектральной плотности мощности(СПМ)и взаимнойспектральной плотности мощности (ВСПМ) выполняется методами периодограмм и коррелограмм.
В исследуемом методе периодограмм СПМ вычисляется как
,
.
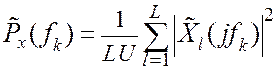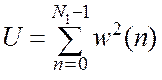Число секций L, по
которому вычисляется усредненная периодограмма 
,
и способ секционирования (разбиения на секции) – с перекрытием или без –
определяют дисперсию или точность получаемых оценок СПМ (ВСПМ) случайных
сигналов. Тип весовой функции и ее длина N1 определяют частотную характеристику канала анализатора
спектра – ширину ее главного лепестка, затухание, эквивалентную шумовую полосу,
от которых зависят частотное разрешение и точность спектрального анализа. Более
подробно с методами спектрального анализа сигналов на основе ДПФ можно
познакомиться в [1, 5, 7].
Если частоты составляющих сигнала априорно известны, то дляих разрешения и оценки параметров нужно выбрать N1 таким образом, чтобы частоты всех составляющих были кратны значению шага анализа по частоте Df= fд/N = fд/N1 при N = N1, т. е. совпадали с частотами анализа или бинами ДПФ. При этом соседние частотные составляющие отстояли бы друг от друга не менее чем на 2Df для прямоугольной весовой функции и 4Df – для весовой функции Хэмминга. От величины N1 зависит также случайная погрешность спектрального анализа зашумленных сигналов.
Задание на подготовку к работе
1. Ознакомиться с целями, задачами и содержанием лабораторной работы.
2. Изучить теоретические сведения к работе.
3. Подготовить исходные данные к лабораторной работе в соответствии с индивидуальным вариантом.
4. Подготовить дополнительные исходные данные к конкретным лабораторным заданиям.
5. Ознакомиться с описанием программного обеспечения к лабораторной работе.
6. Пройти входное тестирование или опрос для допуска к лабораторной работе.
Указания по подготовке исходных данных к лабораторной работе
Исходными данными к лабораторной работе являются значения центральной частоты и граничных частот по уровням –ап, –аз каналов соответствующей многоканальной системы ЦОС. Они определяются центральной частотой foi и частотами среза-задерживания fc1, fc2, fз1, fз2 полосно-пропускающих фильтров, синтезируемых и исследуемых в лабораторных работах №2, 3. Значения этих частот, а также частоты дискретизации fд и допусков на погрешности аппроксимации полосно-пропускающего фильтра ап, аз находятся из таблиц 4–6 в соответствии с индивидуальным вариантом. В данной лабораторной работе они используются при синтезе тестовых сигналов и формирующего нерекурсивного фильтра.
В качестве дополнительных исходных данных ко всем лабораторным заданиям необходимо найти базовое (номинальное) значение ширины окна анализа спектра N1ном, обеспечивающее однозначное разрешение составляющих тестового полигармонического сигнала с частотами foi, fc1, fc2, fз1, fз2. Для этого определяется максимальный шаг анализа по частоте Dfmax, являющийся наибольшим общим делителем для анализируемых частот foi, fc1, fc2, fз1, fз2 и частоты дискретизацииfд. При этом частоты всех составляющих сигнала и дискретизации оказываются кратными шагу анализа Dfmax и совпадают с частотами анализа анализатора спектра на основе ДПФ fk = kDfmax, k = 0, 1, …N1min/2 (с бинами ДПФ). Шагу анализа Dfmax соответствует минимально необходимая ширина окна анализа N1min = fд/Dfmax. В качестве базового (номинального) значения N1ном принимается значение N1ном = N1min, когда частоты соседних составляющих ПГС отстоят друг от друга не менее чем на 2Dfmax и N1ном = 2N1min в случае, когда частоты соседних составляющих ПГС отстоят друг от друга менее чем на 2Dfmax, чтобы обеспечить их однозначное разрешение. Найденному значению N1ном соответствует номинальное значение шага анализ по частоте Dfном= fд/N1ном. Если для заданного набора частот не удается найти шага анализа Dfmax, удовлетворяющего указанным выше условиям, то значения некоторых из частот можно изменить в небольших пределах, при которых такой шаг существует. В процессе исследования значение ширины окна N1 может быть изменено относительно N1ном, в частности, для изучения зависимости результатов анализа от значения N1 или с целью повышения точности и разрешающей способности спектрального анализа.
Пример 1. Значениям частот foi = 55 Гц, fc1 = 52,5 Гц, fc2 = 57,5 Гц, fз1 = = 50 Гц, fз2 = 60 Гц, fд = 500 Гц из условия совпадения их с бинами ДПФ соответствуют Dfmax = 2,5 Гц, N1min = 200; из условия разрешения соседних частотных составляющих им соответствуют Dfном = 1,25 Гц, N1ном = 400 (цифровая обработка сигналов ЭКГ).
Пример 2. Значениям частот foi = 7800 Гц, fc1 = 7000 Гц, fc2 = 8600 Гц, fз1 = 6200 Гц, fз2 = 9400 Гц, fд = 32000 Гц соответствуют Dfном = Dfmax = 200 Гц, N1ном = 160, которые удовлетворяют как условиям совпадения их с бинами ДПФ, так и разрешения соседних частотных составляющих (цифровая обработка аудиосигналов).
Лабораторное задание №1. Исследование амплитудно-фазовых
спектров сигналов с помощью программы SCANA
(гармонический анализ сигналов)
Согласно лабораторному заданию необходимо:
Синтезировать тестовый полигармонический сигнал (ПГС) с наложенным на него шумом или без наложения шума.
Синтезировать полосовой нерекурсивный цифровой фильтр (НЦФ), центральная частота и частоты среза-задерживания которого определяются частотами составляющих ПГС.
Выполнить спектральный (гармонический) анализ тестового сигнала и выходного сигнала фильтра при различных значениях параметров анализатора спектра (ширины окна анализа, начала окна анализа, вида весовой функции, числа усредняемых окон).
Обосновать получающиеся результаты.
Порядок выполнения лабораторного задания
1.1. В программе SCANA установить значение частоты дискретизации сигнала fд и общую длину реализации сигнала Np³ 32×N1ном + N1ном, где N1ном - определенная выше номинальная ширина окна анализа.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.