Исследование преобразований аддитивной смеси сигнала и шума в типовых каскадах радиоканала. Вариант 3, страница 3

;

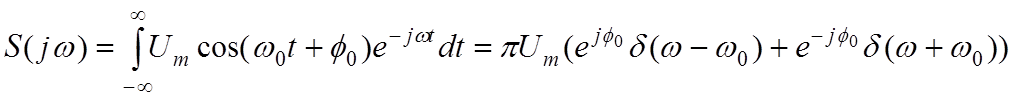
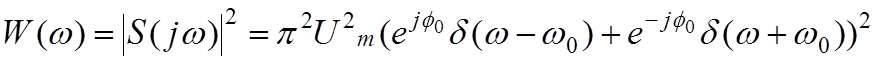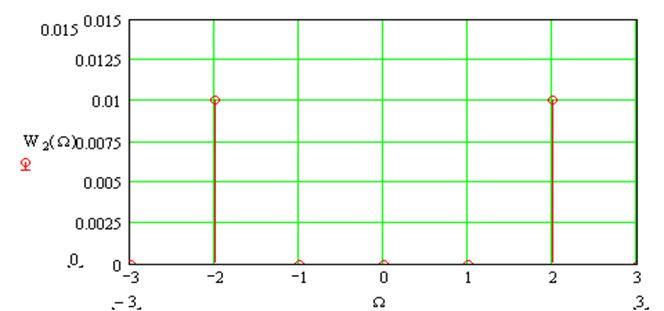
Рис.14.  Энергетический спектр cигнала на выходе ЧД.

Б) Спектр суммарного процесса: W_x2 (W) = W_ξ2 (W) + W₂ (W);

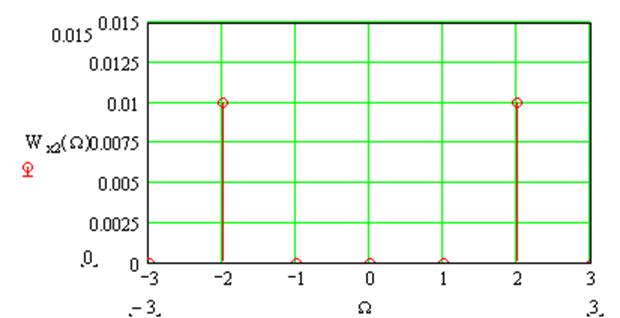Рис.15. Энергетический спектр суммарного процесса на выходе ЧД.

В) Корреляционная функция сигнала на выходе ЧД :

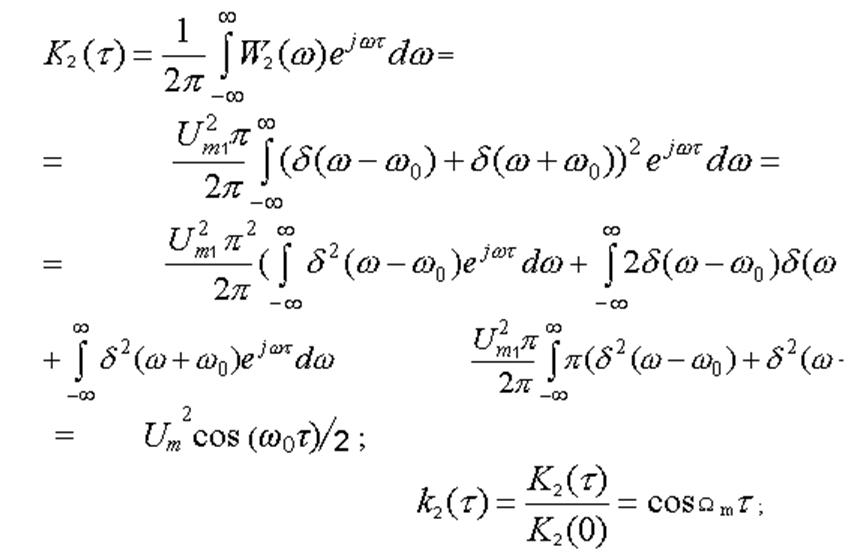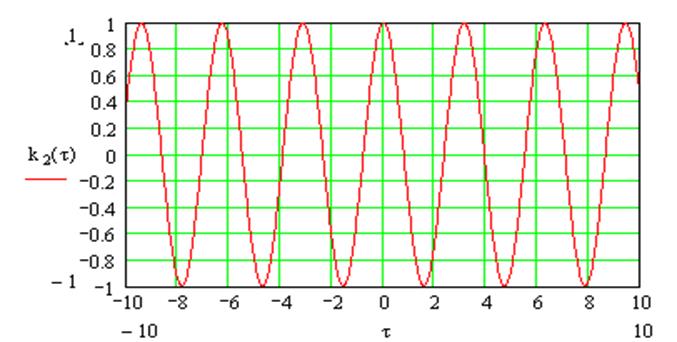Рис.16. Нормированная корреляционная функция сигнала на выходе ЧД.

Г) Нормированная корреляционная функция суммарного процесса:

K_x2(τ) = K₂(τ) + R_x2(t ),  k_x2(τ) = K_x2(τ)/K_x2(0);

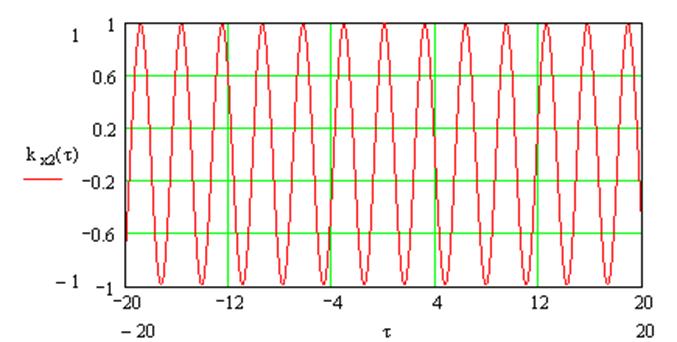Рис.17. Нормированная корреляционная функция суммарного процесса на выходе ЧД.

Д) Дисперсия на выходе ЧД:

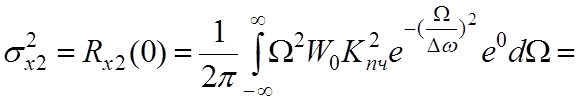 6.347*10^-5  Вт.

4.2.Отношение сигнал/шум на выходе ЧД.

 При U_m²/σ_x2² >> 1, отношение сигнал/шум имеет вид: 

          q₂ = 3(ω_д/W)²q₁,

где q₁– отношение несущая/шум на выходе УПЧ (формула (3.13))

           q₂ = 300*1.77*10³ = 5.31*10⁴;

    – по амплитуде:

a₂ = √2q₂ = 325.57 .

4.3Значение времени корреляции и ширины энергетического спектра процесса на выходе ЧД.

 А) интервал корреляции ( рис.17. ):

τ_к2 = 0.8 с;

 Б) Эффективная ширина спектра ( рис.15. ):

            Δω_эф2= 2*ω_д = 4 рад/с,  Δf_эф= Δω_эф/2π=0.64 Гц.

5. Анализ прохождения  процесса через УНЧ.

    АЧХ УНЧ: |K_нч(jΩ)|² =   K²_нчΔΩ⁴/(ΔΩ² + Ω²)²;                                     (5.1)                                       

1. Для шума.

А) Энергетический спектр шума на выходе УНЧ будет иметь вид:

W_ξ3 (W) = W_ξ2 (W)|K_нч(jΩ)|² =

                       = S_чд²W₀K²_пчW²exp[-(W/Δω)²]K²_нчΔΩ⁴/(ΔΩ² +Ω²)²;      (5.2)

Рис. 18. Энергетический спектр шума на выходе УНЧ.

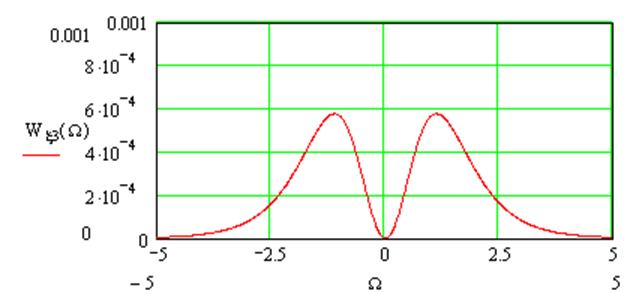Б) Корреляционная функция шума на выходе УНЧ:

                        ΔΩ                                                ΔΩ                                      

R_ξ3(t ) = 1/2π∫W_ξ3 (W)е jWtdΩ = 1/πU_m²∫Ω²W_ξ1(ω₀ + W)е jWtdΩ =

-ΔΩ                                               -ΔΩ

                            ΔΩ                   -(W/Δω)²                                    jWt

     = 1/2πU_m²∫(Ω²W₀K²_пчe     *K²_нчΔΩ⁴/(ΔΩ² +Ω²)²)е  dΩ;                                   (5.3)                                                                                                

-ΔΩ

Этот интеграл возьмем численно, с использованием ЭВМ и пакета MATHCAD.

                      

Рис. 19. Корреляционная функция шума на выходе УНЧ.

2. Для сигнала.

А) Энергетический спектр сигнала на выходе УНЧ будет иметь вид:

W₃ (W) = W₂ (W)|K_нч(jΩ)|²

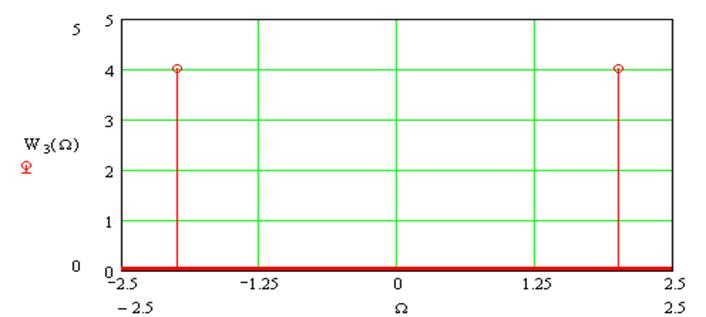Рис. 20. Энергетический спектр сигнала на выходе УНЧ.

Б) Нормированная корреляционная функция сигнала на выходе УНЧ:

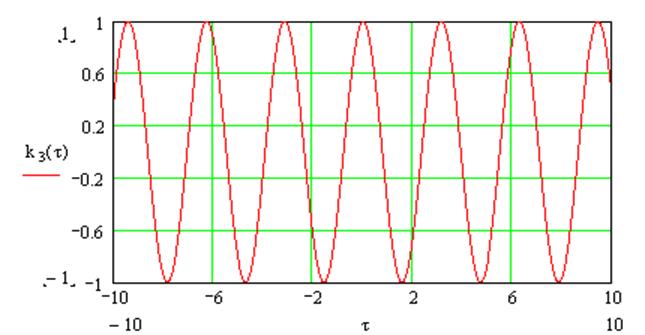Рис. 21. Корреляционная функция сигнала на выходе УНЧ.

3. Для суммарного процесса.

А) Спектр суммарного процесса: W_x3 (W) = W_ξ3 (W) + W₃ (W);

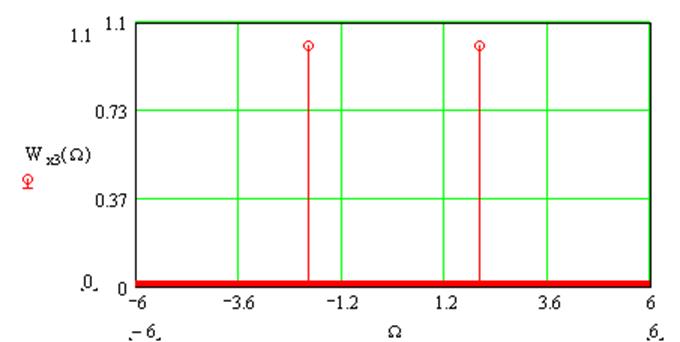Рис.22. Энергетический спектр суммарного процесса на выходе УНЧ.

                               ΔΩ

Б) R₃(t ) = 1/2π∫W₃ (W)е jWtdΩ;

-ΔΩ

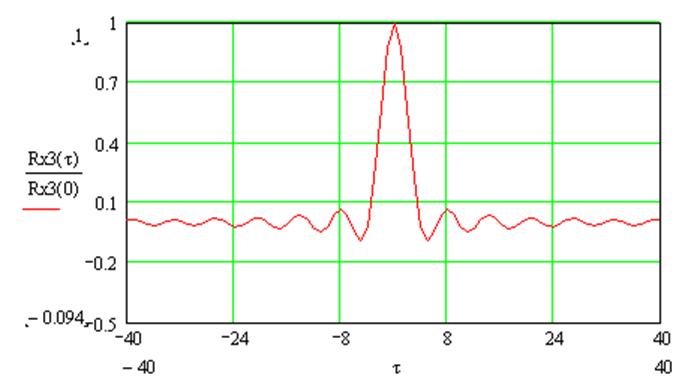
            Рис.23. Нормированная корреляционная функция суммарного процесса на выходе УНЧ.

5.2. Отношение сигнал/шум на выходе УНЧ.

Амплитуда напряжения на выходе УНЧ:

U_m3 = U_m2*K_нч = 2 В;                        

Отношение сигнал/шум по мощности:

q₃ = (½)*U_m3²/σ_x3² = 2²/2*1.141*10^-4= 1.75*10⁴ ;

 -по амплитуде:

a₃ = √2q₃ = 132.45 .      

5.3Значение времени корреляции и ширины энергетического спектра процесса на выходе УНЧ.

А) интервал корреляции ( рис.23. ):

τ_к3 = 2.4 с;

 Б) Эффективная ширина спектра ( рис.22. ):

            Δω_эф3= 2*ω_д = 4 рад/с,  Δf_эф= Δω_эф/2π=0.64 Гц.

Оценка погрешности измеряемого параметра.

Погрешность измеряемого параметра на выходе УНЧ характеризуются мощностью шума на выходе устройства.

 Дисперсия  ( средняя мощность помехи ) на выходе УНЧ:

       σ_x3²= R_x3(0) =

ΔΩ

                 = 1/2πU_m²∫(Ω²W₀K²_пчexp[-(W/Δω)²]K²_нчΔΩ⁴/(ΔΩ² +Ω²)²)dΩ; 

-ΔΩ

 σ_x3²= 1.14*10^-4 Вт;

Погрешность измеряемого параметра не превышает среднеквадратического отклонения помехи:

         σ_x3 = 1.07*10^-2 В . 

Заключение.

 Обобщим результаты исследований:

1. После усилителя и фильтра промежуточной частоты процесс имеет следующие параметры:

амплитуда несущей: U_m1 = 0.6 В;

дисперсия шума составила: σ_x1² = 5.078*10^-6 Вт;

отношение несущая/шум по мощности: q₁ = 3.54*10³;

отношение несущая/шум по амплитуде: а₁ = 59.50;

эффективная ширина спектра: Δf_эф1= 0.64 Гц;

время корреляции: τ_к1 = 6.8*10^-3 с;

2.  Параметры процесса после прохождения через частотный детектор:

амплитуда полезного сигнала: U_m2 = 0.1 В;

дисперсия шума составила: σ_x2² = 6.347*10^-5  Вт;

отношение сигнал/шум по мощности: q₂ = 5.31*10⁴;

отношение сигнал/шум по амплитуде: а₂ = 325.57;

эффективная ширина спектра: Δf_эф2= 0.64 Гц;

время корреляции: τ_к2 = 0.8 с;

3. Параметры процесса после прохождения через усилитель и фильтр нижних частот:

амплитуда полезного сигнала: U_m3 = 1 В;

        дисперсия шума составила: σ_x3²= 1.14*10^-4 Вт;

отношение сигнал/шум по мощности: q₃ = 1.75*10⁴ ;

отношение сигнал/шум по амплитуде: а₃ = 132.45;

эффективная ширина спектра: Δf_эф3= 0.64 Гц;

время корреляции: τ_к = 2.4 с;

Из проведенного анализа можно вывести следующее важное свойство системы с частотным детектором: при заданном спектре помехи на входе устройства, мощность помехи на выходе уменьшается с возрастанием сигнала, т.е. наблюдается подавление помехи сигналом. Подавление помехи сигналом сохраняется, пока обеспечивается полное ограничение амплитуды сигнала на входе детектора и когда помеха слабее сигнала. В противном случае наблюдается подавление слабого сигнала помехой.

Для повышения помехоустойчивости целесообразно применение оптимальной линейной фильтрации, которая заключается в выделении узкой полосы частот соответствующей полезному сигналу.

Литература

1.  Патюков В.Г., Громыко А.И. ”Исследование преобразований аддитивной смеси сигнала и шума в типовых каскадах радиоканала “. Методические указания по курсовому    проектированию. КрПИ, 1992.  № 768.

2.  Гоноровский И.С.  “Радиотехнические цепи и сигналы”.  М.:  Радио и связь, 1986.

3.   Баскаков С.И.  “Радиотехнические цепи и сигналы”.  М.:  Высш. шк., 1988.