Курсовая работа
по РТЦиС
Выполнил студент гр. Р 29-1
Киселев И.И.
Проверил преподаватель
Кашкин В.Б.
Красноярск 2001
1. Постановка задачи ……………………………………………………3
2. Исходные данные ……………………………………………………..3
3. Определение статистических характеристик суммарного процесса
на выходе УПЧ ……………………….…………………………….4
4. Анализ прохождения случайного процесса через ЧД ………………10
5. Анализ прохождения случайного процесса через УНЧ……………..14
6. Заключение...…………………………………………………………....16
7. Литература …………………………………………………………….17
 |
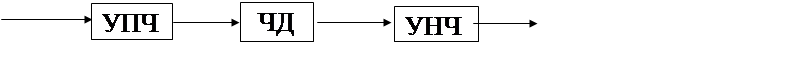Cхема содержит последовательно соединенные первый безинерционный усилитель, узкополосный фильтр, нелинейную цепь, в данном случае частотный детектор, второй безинерционный усилитель и фильтр низкой частоты. Совокупность первого безинерционного усилителя и узкополосного фильтра представляет собой резонансный усилитель промежуточной частоты (УПЧ), который предназначен для выделения полезного сигнала из шумов. Выделение информационного сообщения, заложенного в частоту сигнала, выделяется с помощью нелинейной цепи, т.е. частотного детектора. Второй усилитель и ФНЧ предназначены для выделения полезного сигнала из шумов.
На вход анализируемого устройства (рис. 1)
воздействует аддитивная смесь шума с энергетическим спектром W0: 
, (1.1)
и сигнала c гармонической ЧМ:
S(t)= А1cos[ω0t + (ωд/Ω)cos(Ωt)] = А1cos[ω0t + θ1(t)] = А1cosψ1(t) (1.2)
суммарное колебание можно записать в виде:
s(t)+x(t)=U(t)cos[ω0t +ξ(t)], (1.3)
где огибающая U(t) и фаза ξ(t) определяются выражениями:
Задача сводится к оценки помехоустойчивости.
2. Исходные данные.
Тип детектора: частотный.
-(ω-ωо)2 -(ω+ωо)2
АЧХ УПЧ: 
|Kпч(jω)|2 = (½)*K2пч{ е Δω2
+ е Δω2 }; (2.1)
АЧХ УНЧ: |Kнч(jΩ)|2 = K2нчΔΩ4/(ΔΩ2 + Ω2)2; (2.2)
Кпч=20000; Δω = 5 рад/с; W0=0.009 мкВ2с/рад;
Кнч= 20; ΔΩ = 4 рад/с; Um= 30 мкВ;
ωд = 2 рад/с; Ωm = 0.2 рад/с;
Все найденные характеристики, на выходе УПЧ обозначать индексом 1, на выходе ЧД индексом 2, на выходе УНЧ индексом 3.
3. Определение статических характеристик суммарного
процесса на выходе УПЧ.
3.1. Энергетические характеристики на выходе УПЧ.
А) Найдем энергетический спектр сигнала (1.2) на выходе УПЧ: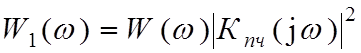 
,
(3.1)
где 
-энергетический спектр сигнала на входе УПЧ.
Выражение (1.2) преобразуем к виду
S(t) = Umcos(θ1(t))cos(ω0t) –Umsin(θ1(t))sin(ω0t); (3.2)
В данном случае θ1(t) = msin(Ωt), тогда
S(t) = Umcos(msin(Ωt))cos(ω0t) – Umsin(msin(Ωt))sin(ω0t); (3.3)
В теории бесселевых функций доказываются соотношения:
sin(msin(Ωt)) = 2J1(m)sin(Ωt) + 2J3(m)sin(3Ωt) + …,
cos(msin(Ωt)) = J0(m) + 2J2(m)cos(2Ωt) + …,
Здесь Jn(m) – бесселева функция первого рода n-го порядка от аргумента m.
С помощью этих соотношений получим в (3.3)
S(t) = Um{J0(m)cos(ω0t) +J1(m)[cos(ω0 + Ω)t) – cos(ω0 – Ω)t)] + J2(m)[cos(ω0 + 2Ω)t) + cos(ω0 – 2Ω)t)] + J3(m)[cos(ω0 + 3Ω)t) – cos(ω0 – 3Ω)t)] + …}
Таким образом, спектр колебания состоит из бесконечного числа боковых частот, расположенных симметрично относительно несущей частотыω0, амплитуда n-ой
составляющей равна Аn =Um*│Jn(m)│. А спектр сигнала запишем в виде:
∞
S(ω) = ∑ Аn ; (3.4)
n=0
 |
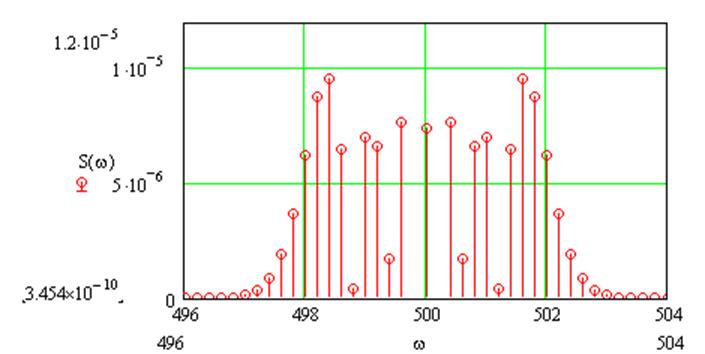Рис.2. Cпектр сигнала в области положительных частот.
Теперь найдем энергетический спектр сигнала на входе УПЧ
 |
= S2(ω), c учетом (3.4) получаем:
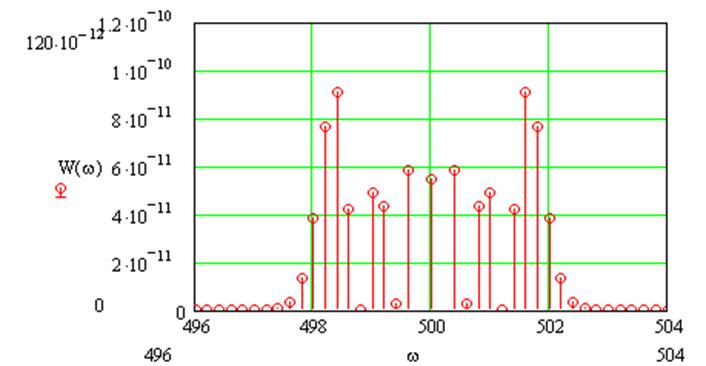Рис.3. Энергетический спектр сигнала .
И энергетический спектр сигнала на выходе УПЧ:
 |
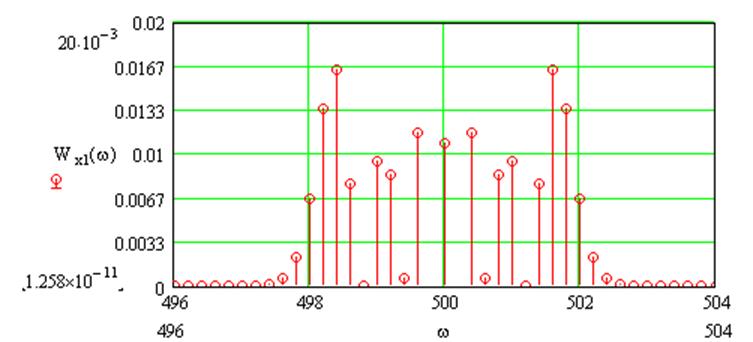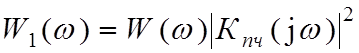= S2(ω)*(½)*K2пч{ е Δω2 + е
Δω2 }; (3.5)
Рис.4. Энергетический спектр сигнала на выходе УПЧ.
Б) Энергетический спектр шума на выходе УПЧ:
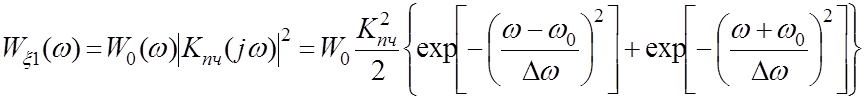
(3.6)
 |
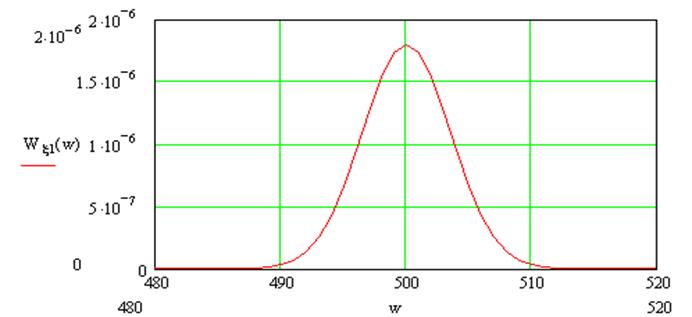Рис.5. Энергетический спектр шума на выходе УПЧ.
В) Энергетический спектр суммарного сигнала на выходе УПЧ.
Т.к. УПЧ - линейный элемент, то для него справедлив принцип суперпозиций:
Wx1(ω) = W1(ω) + Wξ1(ω), тогда с учетом (3.5) и (3.6) находим:
Wx1(ω) = |Kпч(jω)|2*{W (ω)+ W0(ω)} =
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
