-(ω-ωо)2 -(ω+ωо)2
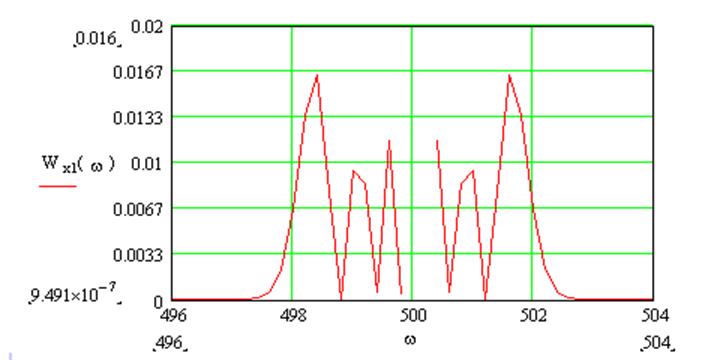 |
Рис.6. Энергетический спектр суммарного процесса на выходе УПЧ.
3.2. Корреляционные функции на выходе УПЧ.
А) Для сигнала, по теореме Винера-Хинчина:
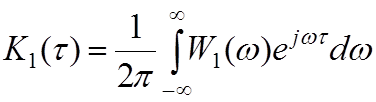 , c
учетом (3.5) получаем:
, c
учетом (3.5) получаем:
K1(τ) = K2пчUm2cos (ω0τ)/4;
нормированная корреляционная функция:
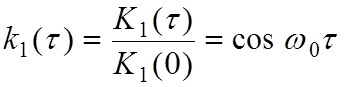 ; (3.8)
; (3.8)
Средняя мощность сигнала на выходе УПЧ:
Pср1 = K1(0) = 0.018 Вт ;
|
Рис.7. Нормированная АКФ сигнала на выходе УПЧ.
Б) Корреляционная функция шума на выходе УПЧ.
Используя преобразование Винера-Хинчина, для шума получим из (3.6):
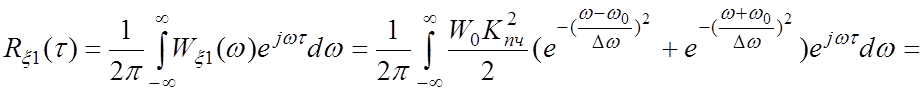
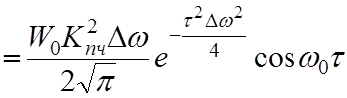 ;
;
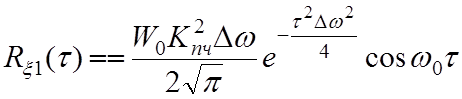 ;
(3.9)
;
(3.9)
нормированная АКФ шума на выходе УПЧ:
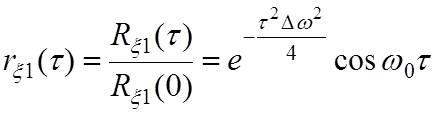 ;
(3.10)
;
(3.10)
Дисперсия шума на выходе УПЧ: σx12= Rξ1(0) = 5.078*10-6 Вт ;
её график приведен на рис.8.
|
Рис.8. Нормированая АКФ шума на выходе УПЧ.
В) Суммарная АКФ на выходе УПЧ.
Используя принцип суперпозиции, справедливый для УПЧ с учетом (3.9) можно записать :
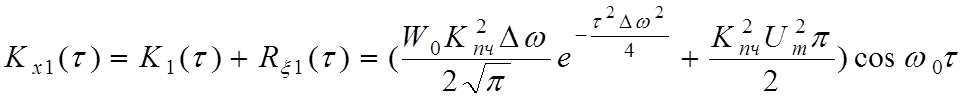 ;
;
Нормированная АКФ суммарного процесса на выходе УПЧ имеет вид:
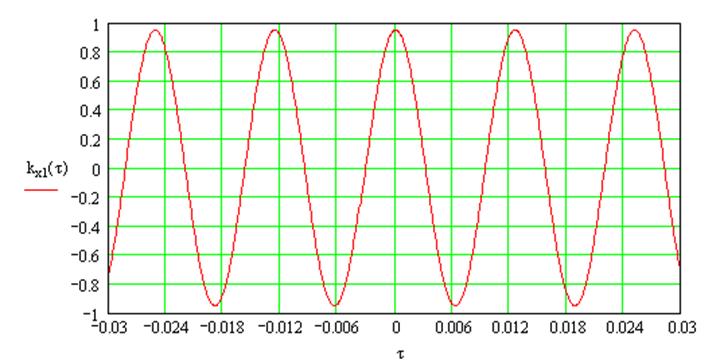 |
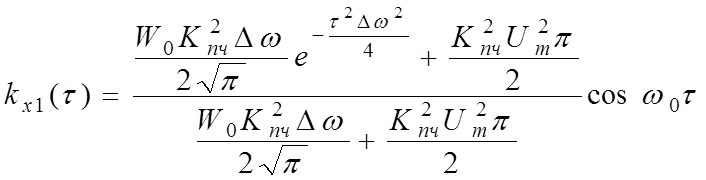 ; (3.11)
; (3.11)
Рис.9. Нормированная АКФ суммарного процесса на выходе УПЧ.
выражение для огибающей АКФ суммарного процесса на выходе УПЧ:
N1(τ)
= 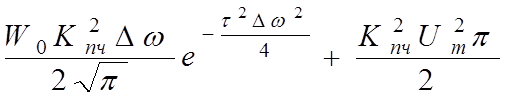 ;
;
8
нормированная огибающая АКФ суммарного процесса на выходе УПЧ:
n1(τ)
= 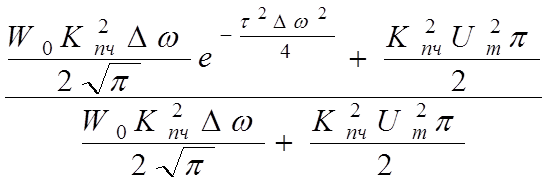 ;
(3.12)
;
(3.12)
график нормированной огибающей АКФ суммарного процесса на выходе УПЧ приведен на рис.10.
|
Рис.10. Нормированная огибающая АКФ суммарного процесса на выходе УПЧ.
3.3Значение времени корреляции и ширины энергетического спектра процесса на выходе УПЧ.
А) интервал корреляции.
Интервал корреляции определим по первому переходу АКФ через ось абсцисс
( рис.9. ):
τк1 = 6.8*10-3 с.
Б) Эффективная ширина спектра .
Ширину энергетического спектра суммарного процесса на выходе УПЧ определим по снижению значений в 1,4 раза от максимального:
Δωэф1= 4 рад/с, Δfэф= Δωэф/2π=0.64 Гц;
3.4. Отношение несущая/шум на выходе УПЧ.
По мощности:
q1 = Pср1/σx12 = 0.018/5.078*10-6= 3.54*103; (3.13)
– по амплитуде:
a1 = √2q1 = 59.50 .
–амплитуда несущей на выходе УПЧ:
Um1 = Um*Кпч = 0.6 В.
4. Анализ прохождения процесса через ЧД.
1. Каждая из реализаций случайного узкополосного процесса имеет вид почти гармонического колебания и может быть записана в виде (1.1) :
![]() ,
,
где А(t)
огибающая, ![]() -фаза,
-фаза, ![]() -частота, случайные функции.
Представим колебание x(t) через квадратичные составляющие:
-частота, случайные функции.
Представим колебание x(t) через квадратичные составляющие:
![]()
![]() ,
,
где ![]() ;
;
![]() ;
;
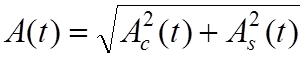 ;
;
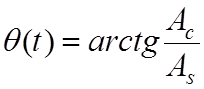 ;
;
А) Закон распределения мгновенной частоты шума на выходе частотного детектора определяется распределением производной фазы :
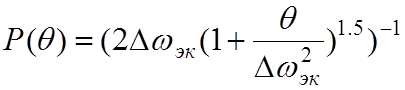 ,
(4.1)
,
(4.1)
величину Δωэк можно определить из уравнения:
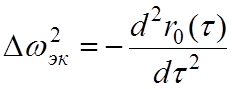 ,
(4.2)
,
(4.2)
где ![]() -огибающая нормированной корреляционной функции rξ1(τ) шума, обладающего спектром
-огибающая нормированной корреляционной функции rξ1(τ) шума, обладающего спектром 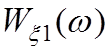 , с учетом (3.10):
, с учетом (3.10): 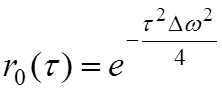 ;
;
Далее определяем вторую производную в левой части уравнения (4.2):
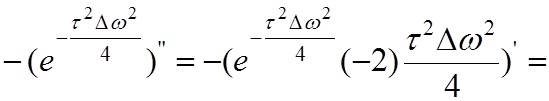
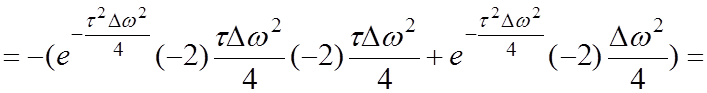
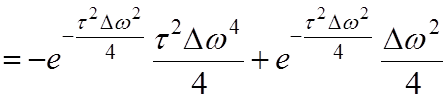 ,
,
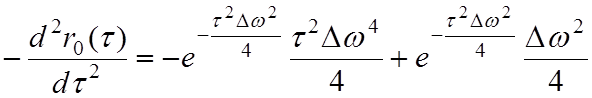 ;
;
получим:
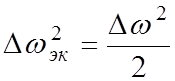 ;
;
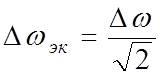 = 3.536 рад/с;
= 3.536 рад/с;
Теперь из (4.1) находим распределение производной фазы и закон распределения частоты шума на выходе ЧД:
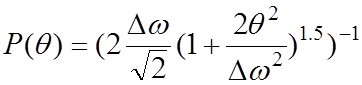 ;
(4.3)
;
(4.3)
|
Рис.11. Закон распределения производной фазы на выходе ЧД.
Б) Энергетический спектр шума на выходе ЧД.
В случае, когда Um2/σx22 >> 1, выражение для фазы можно упростить:
ξ(t) ≈ arctg[A(t)*Sin![]() /As(t)] ≈ A(t)*Sin
/As(t)] ≈ A(t)*Sin![]() /As(t); (4.4)
/As(t); (4.4)
Функция A(t)*Sin![]() обладает нормальным законом
распределения и энергетическим спектром 2Wξ1(ω0 + W) [ 2, §11.6 ]. Таким образом,
энергетический спектр фазы процесса на выходе ЧД:
обладает нормальным законом
распределения и энергетическим спектром 2Wξ1(ω0 + W) [ 2, §11.6 ]. Таким образом,
энергетический спектр фазы процесса на выходе ЧД:
Wq (W) = 2Wξ1(ω0 + W)/Um12 ;
Энергетический спектр производной θ´(t) можно найти, используя правило дифференцирования сигнала [ 2, §.7 ]:
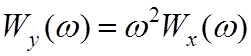 ,
таким образом:
,
таким образом:
Wq´(W) = W2Wq (W) = 2W2Wξ1(ω0 + W)/Um12;
т.к.Xx2(t) = Sчд θ´(t), а также обращаясь к (3.6) можем записать:
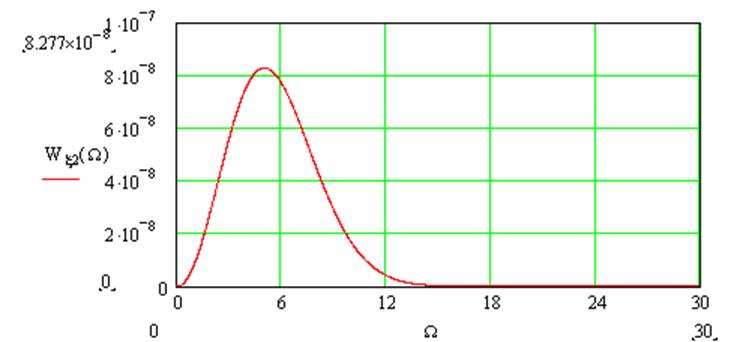
Wξ2 (W) = Sчд2Wq´(W) = 2Sчд2W2Wξ1(ω0 + W)/Um2= Sчд2W0K2пчW2exp[-(W/Δω)2];(4.5)
Учитывая то, что после прохождения детектора сигнал проходит через усилитель и фильтр нижних частот (УНЧ), выберем Sчд равным 0,05 (В*с)/рад, чтобы на выходе УНЧ амплитуда сигнала аходилась в рабочем диапазоне.
 |
В) Дисперсия случайной фазы на выходе ЧД:
σx12= Δω2экσx12/2 = 6.348*10-5 Вт ; (4.6)
Г) Корреляционная функция шума на выходе ЧД:
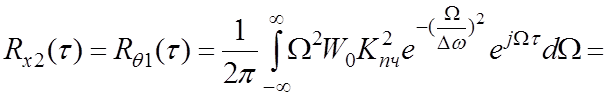
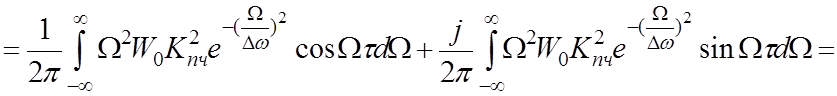
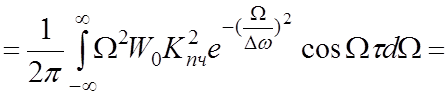
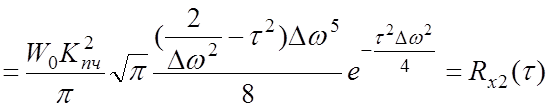 ;
(4.7)
;
(4.7)
Нормированная корреляционная функция шума на выходе ЧД:
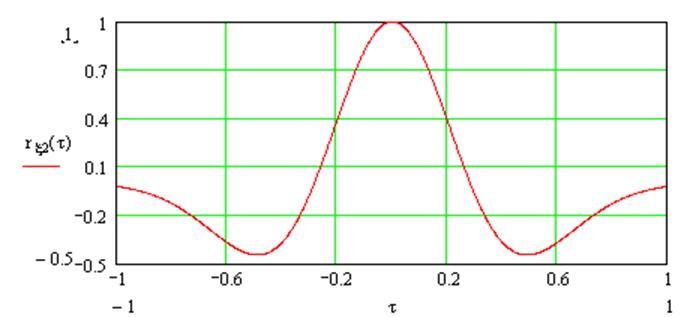 |
Рис.13. Нормированная корреляционная функция шума на выходе ЧД.
2. Для сигнала:
А) Энергетический спектр сигнала на выходе ЧД представляет собой спектр гармонического колебания S2(t) =Um1cos(Ωmt) :
W2(ω)-энергетический спектр сигнала на входе УПЧ. Для его нахождения
применим прямое преобразование Фурье:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.