Алгоритм формирования структурной матрицы цепи. Алгоритм получения матрицы главных сечений. Передаточная функция электронной цепи. Алгоритм получения АЧХ и ФЧХ электронной цепи, страница 3

3.  Проверить правильность ММС, сопоставив размерность матриц  и векторов ,  и .

Лабораторное задание

1.  Ввести схему в ЭВМ.

2.  Получить с помощью ЭВМ матричные коэффициенты  и сравнить их с полученными вручную.

Контрольные вопросы

1.  Что такое компонентные и топологические уравнения?

2.  Какова общая форма ММС по методу переменных состояния?

3.  Какова размерность матричных коэффициентов ?

ЛАБОРАТОРНАЯ РАБОТА 5

Передаточная функция электронной цепи

Цель работы: изучение алгоритмов формирования передаточной функции цепи с одним входом и одним выходом.

Расчет характеристик передачи цепи

Часто I и U в ветвях не находят. Рассматривают лишь отношения I и U в различных точках, находя характеристики передачи цепи. Для этого в исследуемой схеме выделяют точки, называемые входом и выходом. Ко входу подключается источник воздействия  и находится отклик , вызванный им на выходе. Как правило, в схеме оставляют только один источник входного воздействия, закорачивая или размыкая остальные источники.

Передаточная функция RLC-цепи

Под передаточной функцией понимается отношение

,

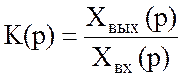где  и  - изображения в р- области  и .

Передаточная функция может быть представлена в дробно-рациональной форме, т. е. в виде дроби, числителем и знаменателем которой являются полиномы p:

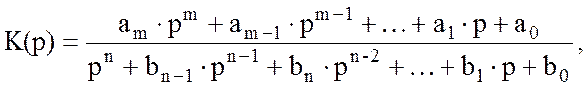
где n – порядок анализируемой схемы.

Для нахождения передаточной функции RLC-цепи используется выражение

Коэффициенты  и  можно найти, используя уравнение отклика цепи:

Обратная матрица  находится с помощью алгоритма Леверрье-Фадеева [2, с. 63-67]

Подготовка к работе

1.  Получить коэффициенты  и , входящие в уравнение отклика цепи.

2.  Используя алгоритм Леверрье-Фадеева, определить коэффициенты a и b для дробно-рациональной формы представления передаточной функции цепи.

3.  Получить передаточную функцию цепи.

Лабораторное задание

1.  Ввести схему в ЭВМ.

2.  Получить коэффициенты a и b, входящие в выражение для передаточной функции цепи.

Контрольные вопросы

1.  Как находятся коэффициенты  и  уравнения отклика цепи для резистивной выходной ветви?

2.  Коэффициенты  и  для реактивной выходной ветви.

3.  Коэффициенты  и  для выходной цепи, состоящей из нескольких ветвей произвольного типа.

4.  Для чего используется алгоритм Леверрье-Фадеева?

ЛАБОРАТОРНАЯ РАБОТА 6

Алгоритм получения АЧХ и ФЧХ электронной цепи

Цель работы: изучение алгоритмов получения АЧХ и ФЧХ схемы.

Алгоритм расчета частотных характеристик с использованием передаточной функции цепи

Комплексный коэффициент передачи, зависящий от частоты воздействия ω, может быть получен по уже известной передаточной функции, представленной в дробно-рациональной форме, простой заменой в ней p на jω:

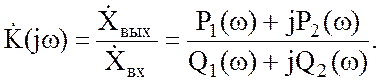
где

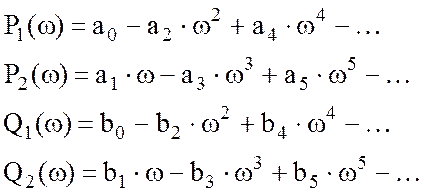
Представим  в показательной форме:

Функция частоты  – амплитудно-частотная характеристика (АЧХ).

Функция частоты  – фазо-частотная характеристика (ФЧХ).

Преобразовывая  можно получить выражения для получения АЧХ и ФЧХ с использованием передаточной функции:

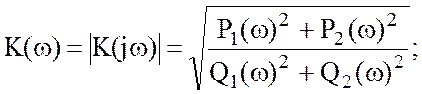
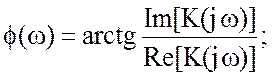
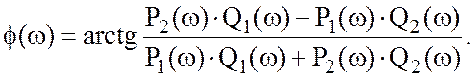
Для построения АЧХ и ФЧХ задаются последовательно значениями частоты ω и при каждой ω рассчитывают P₁, P₂, Q₁, Q₂. Далее можно найти значения АЧХ и ФЧХ. Квадрант, в котором находится угол , определяется по сочетанию знаков значений числителя и знаменателя в выражении для ФЧХ.

Данный метод получения частотных характеристик не требует больших затрат машинного времени и может быть использована особенно в том случае, когда ранее найдена переходная характеристика.

Расчет ЧХ с использованием уравнений состояния

В этом методе для получения рабочих выражений используются уравнения состояния и отклика цепи:

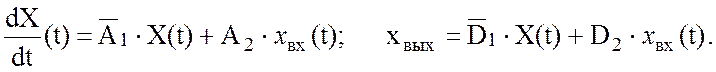
В том случае, если входное воздействие гармоническое, то и все переменные в этих уравнениях являются гармоническими. Представим эти переменные в комплексной форме [3, с. 48-54]:

Для нахождения комплексного коэффициента передачи 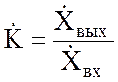 положим, что X_вх =1. Тогда , и уравнения могут быть переписаны в виде:

                                    (8)

Представим вектор состояния  и комплексный коэффициент передачи цепи , входящие в качестве переменных в эти уравнения, в виде:

Приравнивая действительные и мнимые части в (8), получаем систему уравнений:

(9)

(10)

(11)

(12)

Решая систему уравнений (9), (10) на каждой новой частоте, для которой надо определить значение искомой характеристики, находим  и . Далее из (11) и (12) определяем значения  и . Теперь можно найти значения АЧХ и ФЧХ:

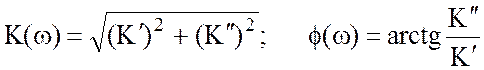
Использование этого метода требует значительных затрат машинного времени, так как требуется решать систему уравнений (9) и (10) на каждой частоте, для которой находятся значения АЧХ и ФЧХ. Целесообразно применять этот метод в том случае, когда постоянные времени анализируемой цепи имеют большой разброс. Это может привести к тому, что нахождение передаточной характеристики будет затруднено или

невозможно. Метод можно использовать и в том случае, когда ЧХ находится для небольшого количества значений частоты, а переходная характеристика ранее не находилась.

Подготовка к работе

Используя какой-либо алгоритм, получить значение АЧХ и ФЧХ для одного номинала частоты. Обосновать выбор этого номинала и используемого алгоритма получения АЧХ и ФЧХ.

Лабораторное задание

Получить АЧХ и ФЧХ анализируемой схемы с помощью ЭВМ.

Контрольные вопросы

1.  Алгоритм расчета АЧХ и ФЧХ, использующий уравнения состояния цепи.

2.  Алгоритм, использующий передаточную функцию цепи.

3.  В каких случаях используется тот или иной алгоритм получения частотных характеристик цепи?

4.  Расчет коэффициентов  и  в алгоритме, использующем уравнения состояния цепи.

ЛИТЕРАТУРА

1.  Автоматизация схемотехнического проектирования. Метод. указания по контрольной работе для студентов заочного факультета специальности 23.01 / Сост. С. И. Дингес; КрПИ.- Красноярск, 1990. -23 с.

2.  Методы автоматизированного расчета электронных схем в технике связи: Учеб. пособие для вузов / Б. А. Калабеков, В. Ю. Лапидус,
В. М. Малафеев. -М.: Радио и Связь. 1990. -272 с.

3.  Атабеков Г. И. Основы теории цепей. Учебник для вузов. -М.:Энергия, 1969. -424 с.