Информатика и выч. техника \ Основы комплексного проектирования и моделирования радиоэлектронных систем

Алгоритм формирования структурной матрицы цепи. Алгоритм получения матрицы главных сечений. Передаточная функция электронной цепи. Алгоритм получения АЧХ и ФЧХ электронной цепи, страница 2

Математическая модель схемы (ММС) представляет собой в общем случае систему интегро-дифференциальных уравнений, описывающих с достаточной степенью точности процессы, происходящие в схеме и ее свойства. Методики формирования ММС в явной (метод переменных состояния) и неявной (метод узловых потенциалов) форме приведены в [1, с.12-17].

Подготовка к работе

Сформировать математические модели RLC-цепи в явной и неявной форме

Контрольные вопросы

1.  Каково количество уравнений в ММС, формируемой в явной форме и неявной?

2.  Преимущества и недостатки обеих форм ММС.


ЛАБОРАТОРНАЯ РАБОТА 3

Алгоритм получения матрицы главных сечений

Цель работы: изучение алгоритмов формирования матрицы главных сечений и ее свойств.

Алгоритм формирования в ЭВМ матрицы главных сечений

Формирование матрицы главных сечений производится в два этапа:

1.  Формируется структурная матрица .

2.  Путем преобразования матрицы  получаем .

В соответствии с законом Кирхгофа для токов . Для получения  надо данную систему уравнений разрешить относительно токов ребер. Это может быть выполнено с помощью метода исключения переменных: из всех уравнений, кроме первого, исключается ток i1. Затем из всех уравнений, кроме второго, исключается ток i2 и т. д. Полученная система уравнений разрешается относительно токов ребер. Таким образом, происходит переход от системы уравнений  к системе .

Применительно к матрицам эта операция исключения переменных преобразует матрицу  так, что в левой ее части образуется единичная матрица, а правая ее часть представляет искомую матрицу . Используются операции перестановки строк и столбцов, суммирование и вычитание строк. Эти операции допустимы. Таким образом, осуществляем преобразование:

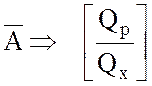 или

Полученную матрицу  можно разбить на подматрицы , сгруппировав элементы матрицы  в соответствии с типами элементов схемы (E, C, R, L, I), к которым они относятся:

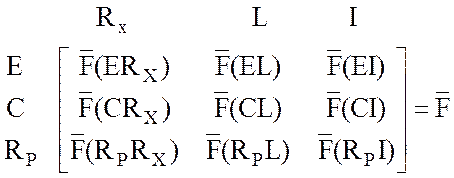
В результате получим общий вид матрицы главных сечений для цепей без особенностей.

Подготовка к работе

1.  Получить матрицу главных сечений анализируемой цепи.

2.  Проверить правильность матрицы, используя два ее основных свойства.

Лабораторное задание

1.  Ввести схему в ЭВМ.

2.  Получить с помощью ЭВМ матрицу главных сечений.


Контрольные вопросы

1.  Какова размерность матрицы главных сечений?

2.  Какие существуют алгоритмы для получения матрицы главных сечений?

3.  Что такое дерево, граф схемы, главное сечение?

4.  Какова общая структура матрицы главных сечений для цепи без особенностей?

5.  Что такое особенности цепи и как влияет их наличие на структуру матрицы главных сечений?

6.  Свойства матрицы главных сечений.

ЛАБОРАТОРНАЯ РАБОТА 4

Алгоритм формирования математической модели схемы по методу переменных состояния. Матричные коэффициенты
.

Цель работы: изучение ММС, получаемой с помощью метода ПС, способа формирования матричных коэффициентов.

Для того чтобы определить поведение RLC-цепи, необходимо знание начальных условий: напряжений на конденсаторах и токов в индуктивностях в начальный момент времени t0. Эти начальные условия и определяют токи в резистивных элементах схемы. Для схем с постоянными параметрами начальное время отсчета t0 может быть взято произвольно, поэтому можно предсказать поведение схемы, зная значения U(C) и I(L) в любой момент времени t0. Следовательно, напряжения на конденсаторах и ток через индуктивности определяют состояние схемы в любой момент времени и называются поэтому переменными состояния. В момент времени t > t0 на резистивные элементы начинают воздействовать еще и источники тока и напряжения. Таким образом, на резистивные элементы RLC-цепи воздействуют источники двух типов:

источники воздействия, которые можно объединить в вектор, называемый вектором источников воздействия: ;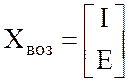

источники замещения реактивных элементов (токи в индуктивных элементах и напряжения на емкостных), входящие в вектор, называемый вектором состояния: .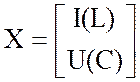

В математическую модель схемы, сформированную по методу переменных состояния, входят два матричных уравнения:


(1)

 


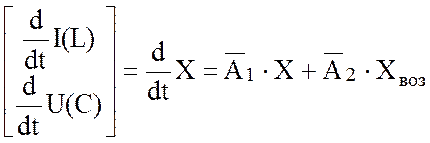(2)

Первое уравнение называется уравнением токов резистивных элементов, второе – уравнением состояния.

Значительную практическую ценность имеет вспомогательное уравнение, в котором определена структура матриц :

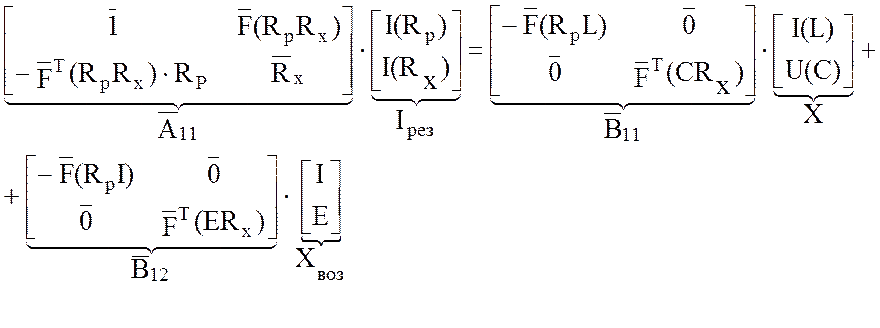
Используя введенные обозначения, получаем:

(4)

Сравнивая (1) и (4), получаем выражения, позволяющие находить значения матричных коэффициентов  и :

При получении этих выражений учтено, что деление на матрицу  равносильно умножению на обратную матрицу :

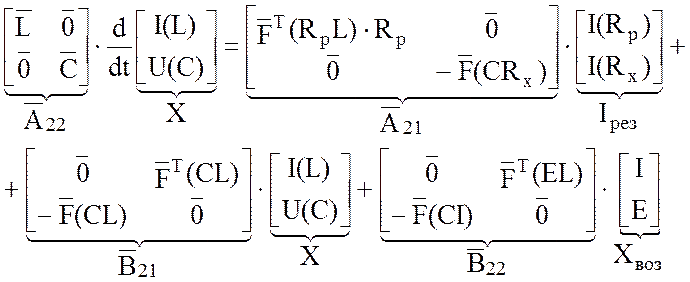
С учетом введенных обозначений

 


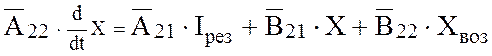(5)


Для нахождения  и :

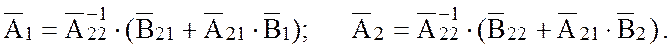
Анализ цепей с большим разбросом параметров элементов

Если анализируемая схема содержит реактивные элементы, величины параметров которых различаются по величине на несколько порядков, нахождение ряда характеристик (АЧХ, ФЧХ, временные характеристики) может быть сильно затруднено. Для устранения этого явления следует учесть диапазон частот, в котором будет производиться анализ цепи. Данный подход приводит к тому, что для каждой цепи могут быть сформированы различные эквивалентные схемы для диапазонов высоких (ВЧ), средних (СЧ), и низких (НЧ) частот. Это позволит снизить порядок анализируемых схем и, следовательно, упростить процесс анализа. Количество диапазонов и их границы выбираются не произвольно, а исходя из конкретных номиналов реактивных элементов.

Преобразование исходной цепи удобно осуществлять пользуясь табл. 1, в которой символ "х" соответствует размыканию, а символ "-" – замыканию соответствующей ветви.

Таблица 1

Lб

Lcp

Lм

Сб

Сср

См

ВЧ

х

х

-

-

СЧ

х

-

-

х

НЧ

-

-

х

х

Подготовка к работе

1.  Получить матричные коэффициенты .

2.  Записать ММС по методу ПС.

Скачать файл