Составление передаточной функции автоматической системы регулирования

Вариант 005

ЗАДАНИЕ НА КОНТРОЛЬНУЮ РАБОТУ

            Исследуемая автоматическая система регулирования режимов работы одного из тепловых объектов задана в виде структурной схемы, передаточных функций звеньев, входящих в систему, а также цифровых данных, характеризующих параметры каждого звена.

          Необходимо составить передаточную функцию автоматической системы регулирования: исследовать систему на устойчивость с помощью критерия Михайлова; пользуясь методом частотных характеристик, рассчитать и построить кривую переходного процесса замкнутой системы регулирования при единичном ступенчатом входном воздействии; сделать выводы о качестве процесса регулирования системы.

W1(p)

W4(p)

W3(p)

х_вх.                                                                                                                                                             f(x)                      x_вых.

 

W2(p)

(-)                     

W2(p)

(-)

 

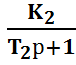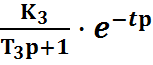W₁(p)= K_1;  W₂(p)= ;  W₃ = ; W₄(p) = .

К₁ = 2,5;      К₂ = 4,0;     К₃ = 5,0;       К₄ = 1,0;

Т₁ = 15,0 с; Т₂ = 10,0 с; Т₃ = 30,0 с;  Т₄ = 40,0 с;

τ = 20,0с.                 = 1

1.  В структурной схеме  АСР обрабатываем внутренние связи и определяем передаточные функции эквивалентных связей.

1.1 Встречно-параллельное соединение или соединение с обратной связью (звенья с передаточными функциями W₂(p) и W₄(p) ).

W1(p)

х_вх.                                                                  х_вых.

                                                                                                           

 

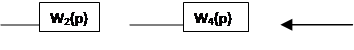В этом случае на вход звена одновременно с входной величиной через звенья обратной связи  W₂ (p), W₄ (p) подается его выходная величина.

W_1,2,4(p) =  =  =  

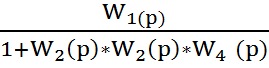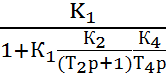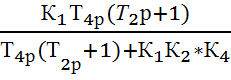
Подставим числовые значения:

W_1,2,4(p) =  =  =

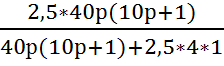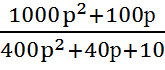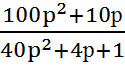
1.2  Последовательное соединение звеньев (звенья с передаточными функциями   W_1,2.4(p), W₃(p)):

W_экв. = W_1,2,4(p) _* W₃(p) =  =

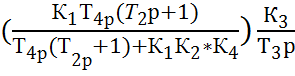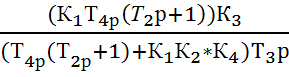
Подставим числовые значения:

W_экв. = =  =

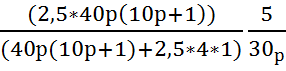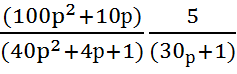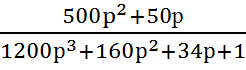
2.  Находим передаточную функцию разомкнутой АСР:

W_р(p) = W_экв.(р) =

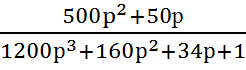
3.    Находим передаточную функцию замкнутой АСР:

W_р(p) =  =  =

.

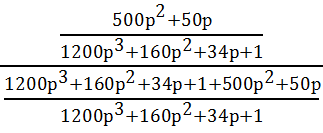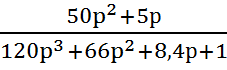4.  Определяем устойчивость АСР по критерию Михайлова.

Передаточная функция замкнутой АСР имеет вид:

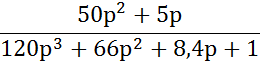
Запишем характеристическое уравнение

Произведем замену в характеристическом уравнении оператора (р) комплексным числом (jω):

W(jω) = 120(jω)³ + 66(jω)² + 8,4(jω) + 1

-120jω³-66ω²+8,4 jω+1=0

Выделим из этого выражения мнимую и вещественную части:

          вещественная часть U(ω) = 1-66ω²;

          мнимая часть   V(ω) =8,4jω-120jω³= j(8,4 ω-120 ω³)

Определяем значения мнимой и вещественной частей выражения при различных значениях ω (от 0до ∞).

Данные расчетов занесем  в таблицу 1.

Таблица 1.

ω	0	0,1	0,2	0,3	0,4	0,5
U(ω)	1	0,34	-1,64	-4,94	-9,56	-15,5
V(ω)	0	0,72	0,72	-0,72	-4,32	-10,8

U(ω):V(ω):

1-66ω² = 1-66*0² =1;                             8,4 ω-120 ω³=8,4*0-  120*0³=0;

1-66ω² = 1-66*0,1² =0,34;                     8,4 ω-120 ω³=8,4*0,1-120*0,1³=0,72;

1-66ω² = 1-66*0,2² = -1,64;                   8,4 ω-120 ω³=8,4*0,2-120*0,2³=0,72;

1-66ω² = 1-66*0,3² = -4,94;                   8,4 ω-120 ω³=8,4*0,3-120*0,3³= -0,72;

1-66ω² = 1-66*0,4² = -9,56;                   8,4 ω-120 ω³=8,4*0,4-120*0,4³= -4,32;

1-66ω²= 1-66*0,5² = -15,5;                 8,4 ω-120 ω³=8,4*0,5-120*0,5³= -10,8.

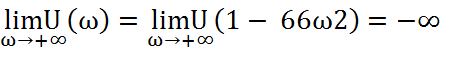
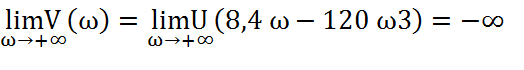
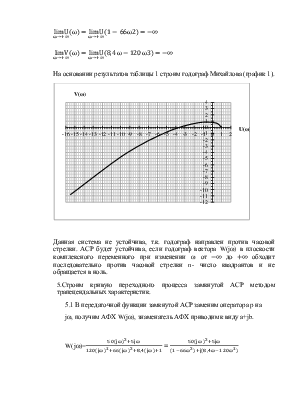
На основании результатов таблицы 1 строим годограф Михайлова (график 1).

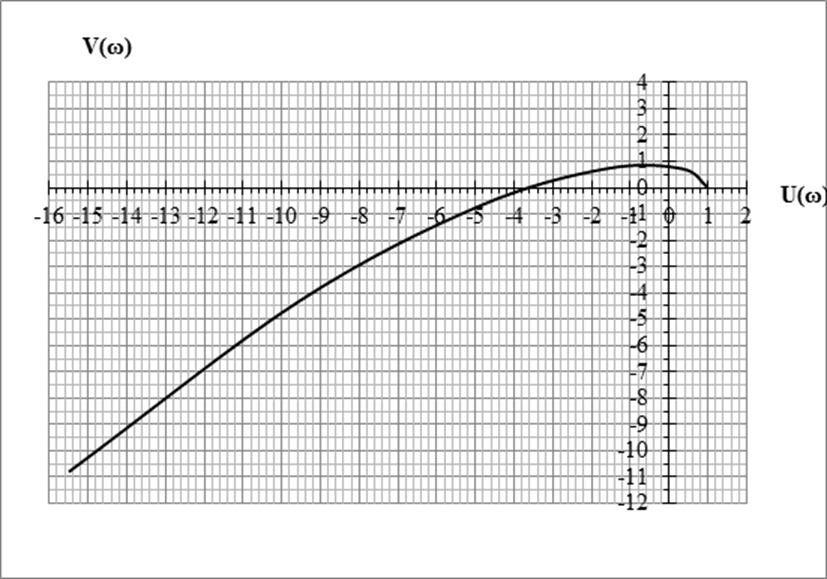
Данная система не устойчива, т.к. годограф направлен против часовой стрелки. АСР будет устойчива, если годограф вектора W(jω) в плоскости комплексного переменного при изменении ω от  до  обходит последовательно против часовой стрелки n- число квадрантов и не обращается в ноль.

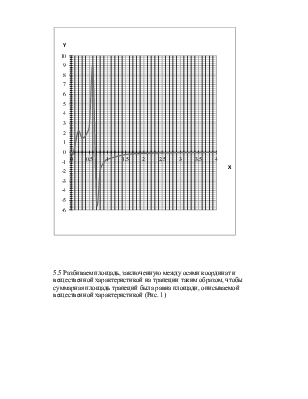
5.Строим кривую переходного процесса замкнутой АСР методом трапецеидальных характеристик.

5.1 В передаточной функции замкнутой АСР заменим оператора р на

jω, получим АФХ W(jω), знаменатель АФХ приводим к виду а+jb.

W(jω)= =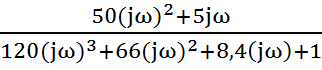

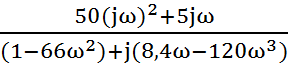
5.2Умножаем числитель и знаменатель на сопряженное комплексное число вида а- jb.

W(jω) =  =

=

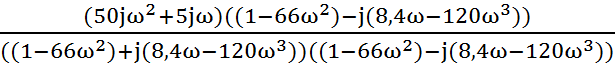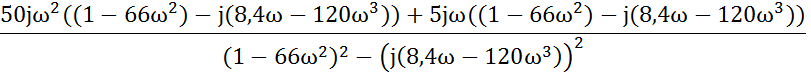
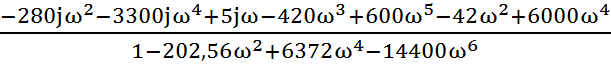
5.3Сгруппируем вещественные и мнимые члены АФХ так, чтобы W(jω)=U(ω)+jV(ω):

W(jω)=+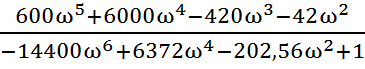

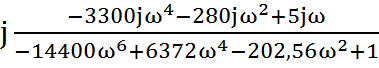
5.4   Выписываем вещественную часть U(ω)=f(ω) и строим график этой зависимости:

U(ω)=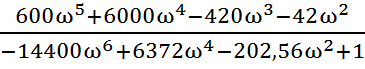

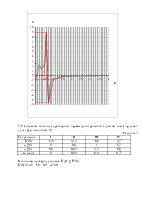
Таблица 2.

ω	0	0,05	0,1	0,2	0,3	0,4	0,5	0,6
U(ω)	1	-0,2247	0,5809	2,1886	1,4627	1,7343	2,6757	8,7565

ω	0,7	0,8	0,9	1	1,5	2	2,5	3
U(ω)	-5,2453	-1,8648	-1,0868	-0,7458	-0,2527	-0,1361	-0,0875	-0,0621