








1 МОДЕЛИРОВАНИЕ НА МИКРО УРОВНЕ
1.1 Струнный датчик натяжения: принцип работы и конструкция
Струнные датчики в настоящее время используются в океанографических исследованиях, а также для измерения напряжений в стали и бетоне, углов поворта и моментов вращения, дилатометрических измерений температуры. Разработанный нами датчик натяжения на основе вибрирующей струны применялся в качестве измерителя силы в термовесах а также при изучении взаимодействия образца с магнитным полем.
Внешний вид датчика показан на рисунке 1, конструкция схематически изображена на рисунке 2.

Рисунок 1 – Внешний вид струнного датчика натяжения
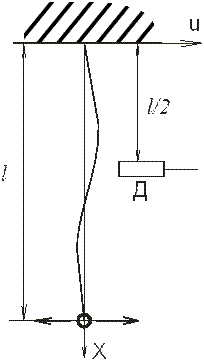
Рисунок 2 – Конструкция струнного датчика
Основной элемент струнного датчика – колеблющаяся струна длиной l, один конец которой закреплен, на другой действуют колебания с частотой n и амплитудой А. На расстоянии l/2 от конца струны находится датчик перемещений (Д) в перпендикулярном направлении.
1.2 Выбор уравнения и его идентификация
Система с распределенными параметрами (СРП) – это система, в которой практически все сигналы (особенно входной и выходной) зависят от пространственных координат и времени.
Есть среды, которые не могут быть описаны в сосредоточенных параметрах (электромагнитное поле, электростатическое поле, течение потока, гравитационное поле, температура и т.д.).
Система с сосредоточенными параметрами является частным случаем СРП и вводится для упрощения и решения задач на первом (нулевом) этапе.
Функция состояния Q(x,t) объекта СРП
(ОРП), определяемая по пространственной переменной ![]() замкнутой
области
замкнутой
области ![]() удовлетворяет уравнению:
удовлетворяет уравнению:
![]()
![]()
![]() (1)
(1)
где ![]() - открытая часть области D, не
содержащая границы;
- открытая часть области D, не
содержащая границы;
L – некоторый заданный оператор (линейная функция Q, в частных производных Q(x,t) различных порядков, интегральный оператор от Q(x,t) и/или x, t).
Конечной задачей решения уравнения СРП является нахождение величины переменной состояния ОРП Q(x,t) в любой момент времени (t>0) в точке X.
Механические колебания струны описываются волновым уравнением, моделирующим процессы распространения свободных колебаний:
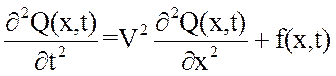 ;
; ![]() ;
;
![]() ;
; ![]() ,
(2)
,
(2)
где x – единственная координата, измеряемая вдоль перемещения колебаний, м;
Q(x,t) – отклонение струны от установившегося состояния, м;
V – скорость распространения волны, м/с;
f(x,t) – удельная сила, действующая на струну в процессе колебаний, Н/кг;
x0 и x1 – начальная и конечная координаты струны, м.
Примем координату верхнего конца x0=0, и будем считать, что в процессе колебаний на струну не действуют силы: f(x,t)=0.
Скорость распространения волны определяется выражением:
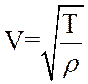 , (3)
, (3)
где T – сила натяжения струны, Н (примем T=1H);
![]() - линейная плотность массы, то есть масса,
приходящаяся на единицу длины струны, кг/м.
- линейная плотность массы, то есть масса,
приходящаяся на единицу длины струны, кг/м.
Будем считать струну цилиндром, тогда линейная плотность рассчитывается по формуле:
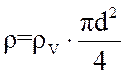 , (4)
, (4)
где ![]() - объемная плотность вольфрама,
кг/м3 (
- объемная плотность вольфрама,
кг/м3 (![]() =19*103
кг/м3);
=19*103
кг/м3);
d – диаметр струны, м (d=10-4м);
Подставив значения, получаем значение скорости: V=81.861м/с.
Для того, чтобы Q(x,t) было однозначно определено в любой точке струны и в любой момент времени, необходимо задать граничные условия на концах струны и начальные условия в момент времени t=0.
Определим граничные условия на концах струны длиной l=0.05м. Один конец жестко закреплен, а другой колеблется по заданному закону входного воздействия:
![]() =
=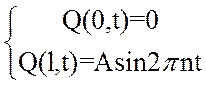 , t>0 (5)
, t>0 (5)
Начальные условия нулевые – в начальный момент времени струна покоится:
N[Q(x,t)]=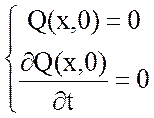 ,
, ![]() (6)
(6)
1.3 Расчет статической характеристики
Уравнение вида (1) с начальными и граничными условиями практически не разрешимо. Для его решения вводится в рассмотрение так называемая стандартная форма записи. Она подразумевает нулевые граничные и начальные условия.
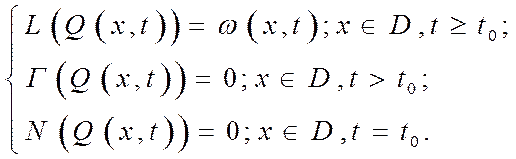 (7)
(7)
где w(x, t) – стандартизующая функция.
Функцией, описывающей реакцию самой
системы, является функция Грина ![]() . Функцией Грина
называется функция источника, которая равна выходному сигналу:
. Функцией Грина
называется функция источника, которая равна выходному сигналу:
![]() ,
при
,
при ![]() , (8)
, (8)
где ![]() - пространственная d - функция.
- пространственная d - функция.
![]() - d - функция по времени;
- d - функция по времени;
x – координаты входного возмущения;
x - координаты точки отклика от удара.
Зная стандартизирующую функцию и функцию Грина, можно найти выходную функцию по следующему выражению:
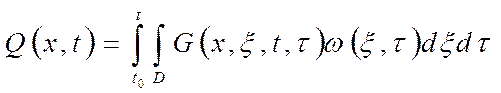 (9)
(9)
Запишем стандартизирующую функцию ![]() и функцию Грина G(
и функцию Грина G(![]() )
на основании выбранного уравнения, начальных условий и входного воздействия по
справочным материалам [1]:
)
на основании выбранного уравнения, начальных условий и входного воздействия по
справочным материалам [1]:
![]() ,
, ![]() , t>0 (10)
, t>0 (10)
G(![]() )=
)=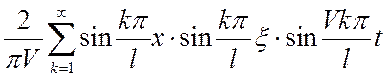 (11)
(11)
Выходная величина Q(x,t) находится как
пространственно временная композиция от произведения функции Грина G(![]() )
на стандартизирующую функцию
)
на стандартизирующую функцию ![]() :
:
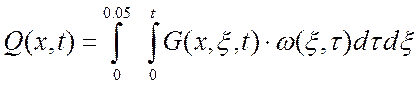 (12)
(12)
Подставим функцию Грина и вынесем сумму из-под интегралов:
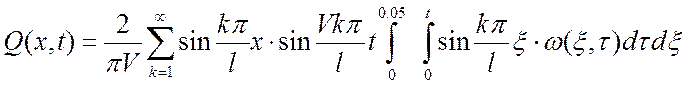 (13)
(13)
Подставим стандартизирующую функцию ![]() :
:
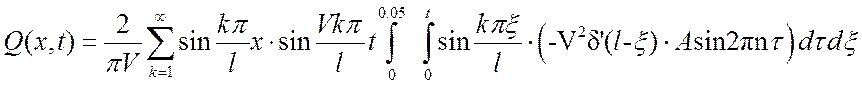 (14)
(14)
Вынесем из-под пространственного
интеграла члены, не зависящие от ![]() :
:
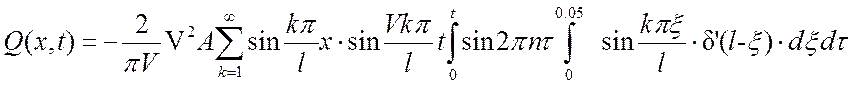 (15)
(15)
Используя свойство ![]() -функции
-функции 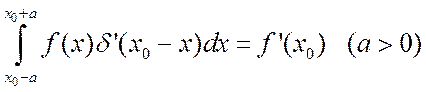 ,
запишем:
,
запишем:
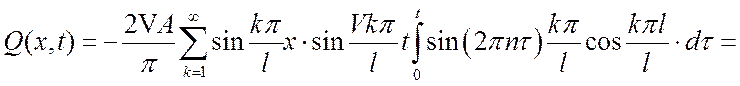
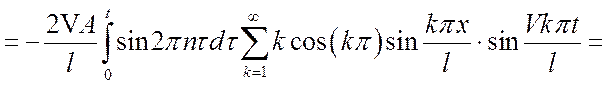
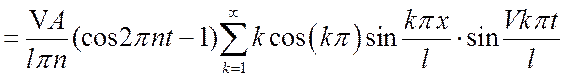 (16)
(16)
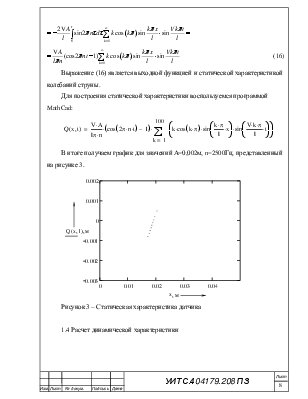
Выражение (16) является выходной функцией и статической характеристикой колебаний струны.
Для построения статической характеристики воспользуемся программой MathCad:
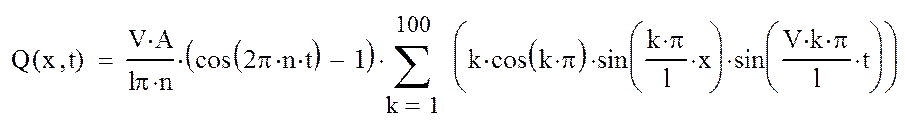
В итоге получаем график для значений А=0,002м, n=2500Гц, представленный на рисунке 3.
![]()
![]()
|
|
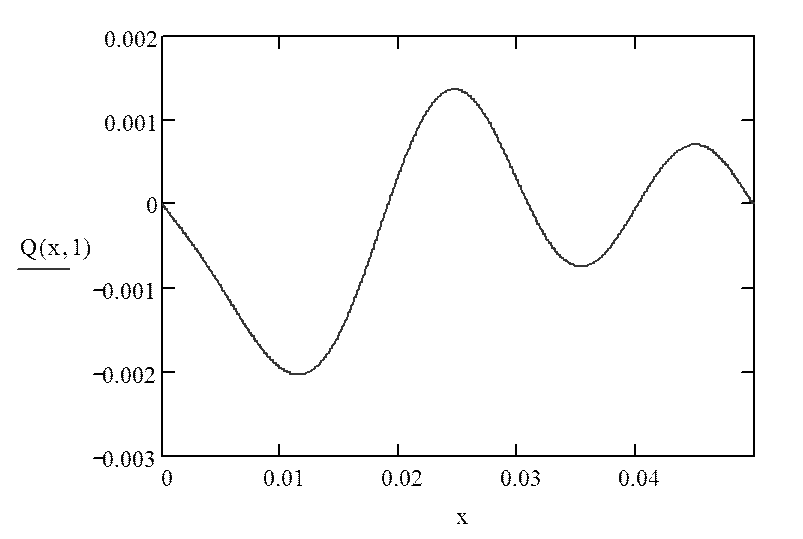
Рисунок 3 – Статическая характеристика датчика
1.4 Расчет динамической характеристики
Динамическая характеристика находится
по интегральной передаточной функции, которая рассчитывается как
пространственная композиция от произведения континуальной передаточной функции ![]() и от преобразованной по Лапласу
стандартизирующей функции
и от преобразованной по Лапласу
стандартизирующей функции 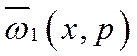 с выделенным из нее входным воздействием:
с выделенным из нее входным воздействием:
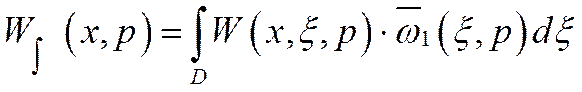 (17)
(17)
Из нормирующей функции ![]() можно выделить в явном виде через компоненту
входной координаты
можно выделить в явном виде через компоненту
входной координаты ![]() требуемую
требуемую 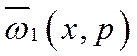 :
:
![]() (18)
(18)
Поскольку
в нашем случае нет возмущающих воздействий, примем ![]() , тогда
, тогда ![]() .
.
Континуальную передаточную функцию находим по справочным материалам [1]:
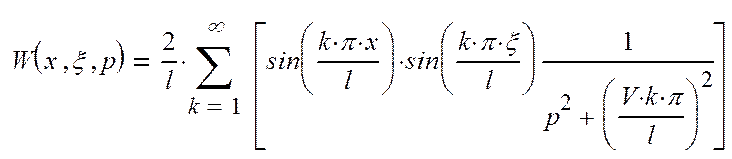 (19)
(19)
Найдем изображение стандартизирующей функции по Лапласу:
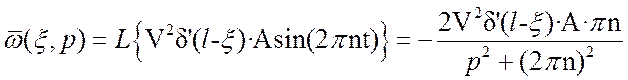 (20)
(20)
В соответствии с выражениями (18)-(20) запишем:
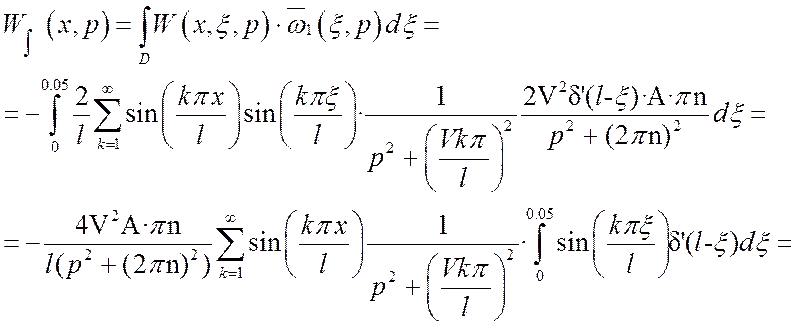
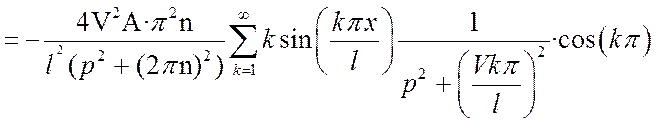 (21)
(21)
Найдем характеристику полученной функции в точке x=l/2:
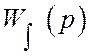 =
= 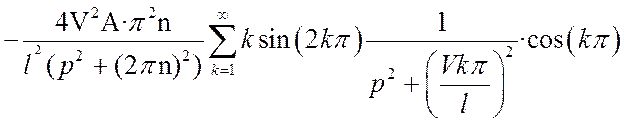
Для выбранной выходной переменной построим ЛАЧХ. При этом необходимо получить частотную форму записи передаточной функции, для этого произведем замену р=jw, и найти ЛАЧХ по выражению:
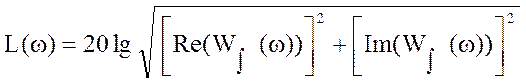 (22)
(22)
Для построения характеристики используем программу MathCad:
|
|
|
|
|
|
Полученная
ЛАЧХ представлена на рисунке 4. Аппроксимируем ее стандартными типовыми
наклонами. Получили наклон -40дБ/дек, что соответствует колебательному звену с
резонансной частотой ![]() Гц. В общем случае
колебательное звено имеет вид:
Гц. В общем случае
колебательное звено имеет вид:
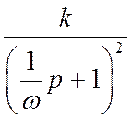 (23)
(23)
Из ЛАЧХ можно сделать вывод, что усиление равно:
![]() (24)
(24)
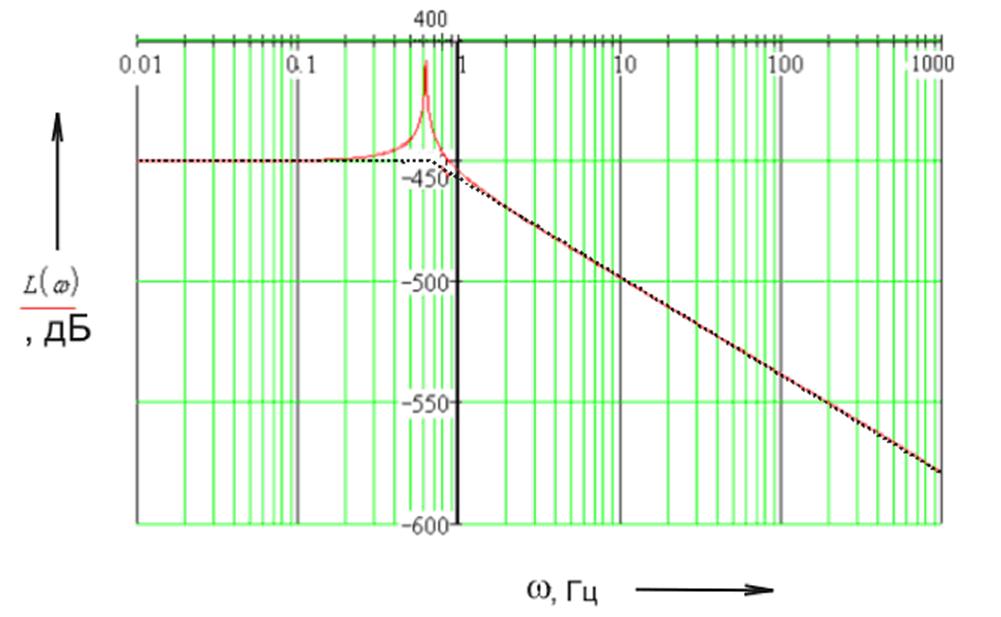
Рисунок 4 – ЛАЧХ струнного датчика натяжения.
С помощью аппроксимации передаточная функция запишется в виде:
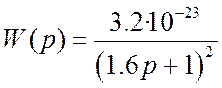
1.5. Моделирование струны в среде ELCUT 5.2
С помощью программы ELCUT можно моделировать задачи магнито- и электростатики, электрических и магнитных полей, задачи теплопередачи и упругих деформаций.
Смоделируем
поведение струны при максимальном отклонении незакрепленного конца струны (![]() ). Для этого создадим задачу ELCUT упругих напряжений и деформаций,
единицы измерения координат - микрометры. Затем построим плоскую модель струны
– прямоугольник с размерами 100х50000 (0.1мм х 50мм). Затем
зададим материал блока в свойствах: для вольфрама модуль Юнга равен 3,5·105МПа=3,5·1011
Н/м2 (3.5e+11). Для левого ребра перемещения равны нулю, для правого
задаются как постоянное значение
). Для этого создадим задачу ELCUT упругих напряжений и деформаций,
единицы измерения координат - микрометры. Затем построим плоскую модель струны
– прямоугольник с размерами 100х50000 (0.1мм х 50мм). Затем
зададим материал блока в свойствах: для вольфрама модуль Юнга равен 3,5·105МПа=3,5·1011
Н/м2 (3.5e+11). Для левого ребра перемещения равны нулю, для правого
задаются как постоянное значение ![]() (2мм). Затем
выполняем команду «Решить задачу», результат решения показан на рисунке 5. Для
наглядного анализа результатов воспользуемся цветовой картой. Критерием выберем
главное напряжение
(2мм). Затем
выполняем команду «Решить задачу», результат решения показан на рисунке 5. Для
наглядного анализа результатов воспользуемся цветовой картой. Критерием выберем
главное напряжение ![]() - это максимальное
напряжение, которое испытывает струна в данной точке. Как видно из цветовой
картины (рисунок 6), максимальные напряжения струна испытывает на ее концах, с
помощью просмотра локальных значений поля получим максимальное напряжение в
струне: 2,14·105 Н/м2. Аналогично можно судить и о
значениях других величин (деформации, перемещений, различных напряжений и
критериев прочности), которые можно также сохранять в отдельный файл.
- это максимальное
напряжение, которое испытывает струна в данной точке. Как видно из цветовой
картины (рисунок 6), максимальные напряжения струна испытывает на ее концах, с
помощью просмотра локальных значений поля получим максимальное напряжение в
струне: 2,14·105 Н/м2. Аналогично можно судить и о
значениях других величин (деформации, перемещений, различных напряжений и
критериев прочности), которые можно также сохранять в отдельный файл.

Рисунок 5 – Моделирование смещений струны от начального положения.
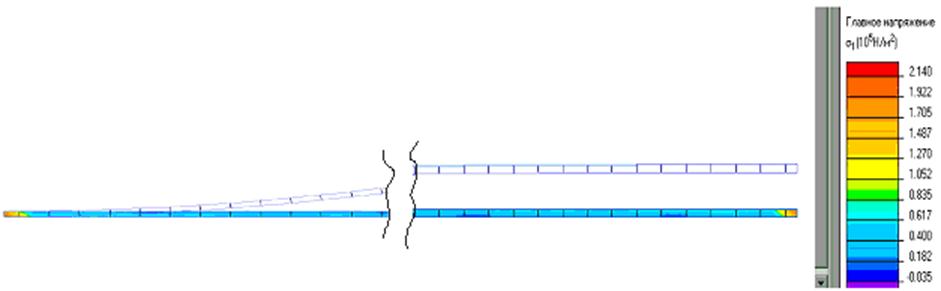
Рисунок 6 – Графическое представление напряжений в струне
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.