Величины относительных нормальных ускорений определяем по формулам:
![]()
Где ![]() - длины векторов на плане
скоростей, мм; АВ - размер звена, м.
- длины векторов на плане
скоростей, мм; АВ - размер звена, м.
Нормальные составляющие ускорения направлены вдоль осей соответствующих звеньев к той точке, движение которой уже известно.
Решение первого уравнения системы: из конца вектора ![]() проводим параллельно звену АВ,
в сторону от точки В к точке А, вектор
проводим параллельно звену АВ,
в сторону от точки В к точке А, вектор ![]() , Через конец вектора проводим
прямую, перпендикулярную к оси звена АВ. Эта прямая будет линией действия касательной составляющей ускорения
, Через конец вектора проводим
прямую, перпендикулярную к оси звена АВ. Эта прямая будет линией действия касательной составляющей ускорения
![]() .
.
Для решения второго уравнения системы из
полюса ![]() параллельно звену ВО
параллельно звену ВО![]() в сторону от точки В к точке О
в сторону от точки В к точке О![]() строим вектор нормального ускорения
строим вектор нормального ускорения ![]() . Линию действия
касательной составляющей ускорении
. Линию действия
касательной составляющей ускорении ![]() . проводим через конец вектора
. проводим через конец вектора ![]() . перпендикулярно
звену ВО
. перпендикулярно
звену ВО![]() . Точка
. Точка
![]() пересечения
пересечения ![]() и
и ![]() . определит конец
вектора
. определит конец
вектора ![]() , изображающего абсолютное ускорение
точки В.
, изображающего абсолютное ускорение
точки В.
Соединив точки а и в плана ускорений, получим вектор полного относительного ускорения:
![]()
Находим ускорения
центров масс ![]() ,
,![]() и
и
![]() :
:
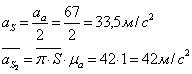 |
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.