Кривошипно-ползунный механизм, кинематический анализ, страница 3

Из произвольно выбранного полюса плана скоростей р откладываем отрезок ра, изображающий скорость точки А, перпендикулярно звену ОА в сторону его вращения.

Переходим к построению плана скоростей структурной группы 2-3, имеющей внешние кинематические пары А и О, и внутреннюю кинематическую пару В. Эта группа относится ко 2 классу 2 порядка 1 вида. Скорость точки А(Vа) уже определена и отложена, а скорость точки равна нулю (неподвижная точка) и будет находится в полюсе плана скоростей.

Для определения скорости внутренней точки В структурной группы составляем систему векторных уравнений:

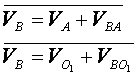Решение первого уравнения системы: проводим из конца вектора  линию действия вектора относительной скорости перпендикулярно звену АВ.

Решение второго уравнения: из полюса , изображающего скорость неподвижной точки О_1, проводим перпендикулярно звену ВОвектор скорости до пересечения с вектором в точке в.

Скорости центров масс  вычисляем путем составления аналогичных пропорций. В случае, когда центры масс находятся посередине звеньев, когда центры масс находятся посередине звеньев, для получения положения  и  на плане скоростей достаточно поделить пополам соответствующие отрезки  и . Соединив точки , и с полюсом плана скоростей Р, получим векторы  представляющие собой абсолютные скорости соответствующих центров масс.

Чтобы найти абсолютное значение скорости какой-нибудь точки, необходимо длину вектора в миллиметрах, изображающего скорость соответствующей точки на плане скоростей, умножить на масштаб плана скоростей.