Резьбовые соединения, выполненные с помощью стандартных крепежных деталей (болтов, винтов, шпилек и гаек)

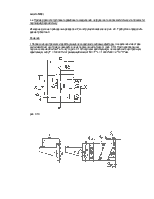
3. Резьбовые соединения

3.1. Общие сведения

Объекты заданий – групповые резьбовые соединения, выполненные с помощью стандартных крепежных деталей (болтов, винтов, шпилек и гаек), имеющих метрическую резьбу с крупным шагом по ГОСТ 9150-81. Основные параметры метрической резьбы показаны на рис. 3.1.

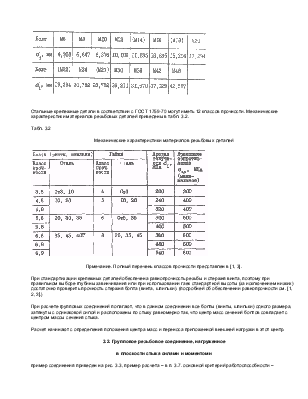
Расчет на прочность стержня болта (винта, шпильки) проводят по диаметру, обозначаемому d₁. Он численно равен внутреннему диаметру резьбы гайки D₁ (рис. 3.2). Значения диаметра d₁ для болтов (винтов, шпилек) с крупной метрической резьбой приведены в табл. 3.1. размеры болтов, заключенные в скобки, менее предпочтительны.

Табл. 3.1

Диаметр болтов (винтов, шпилек) с крупной

метрической резьбой.

Стальные крепежные детали в соответствии с ГОСТ 1759-70 могут иметь 12 классов прочности. Механические характеристики материалов резьбовых деталей приведены в табл. 3.2.

Табл. 3.2

Механические характеристики материалов резьбовых деталей

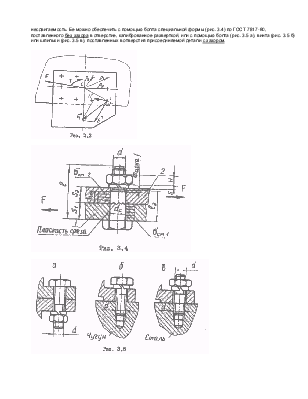
Прмечание. Полный перечень классов прочности представлен в [1, 3].

При стандартизации крепежных деталей обеспечена равнопрочность резьбы и стержня винта, поэтому при правильном выборе глубины завинчивания или при использовании гаек стандартной высоты (за исключением низких) достаточно проверить прочность стержня болта (винта, шпильки). (подробней об обеспечении равнопрочности см. [1, 2, 3].)

При расчете групповых соединений полагают, что в данном соединении все болты (винты, шпильки) одного размера, затянуты с одинаковой силой и расположены по стыку равномерно так, что центр масс сечений болтов совпадает с центром массы сечения стыка.

Расчет начинают с определения положения центра масс и переноса приложенной внешней нагрузки в этот центр.

3.2. Групповое резьбовое соединение, нагруженное

в плоскости стыка силами и моментоми

пример соединения приведен на рис. 3.3, пример расчета – в п. 3.7. основной критерий работоспособности – несдвигаемость. Ее можно обеспечить с помощью болта специальной формы (рис. 3.4) по ГОСТ 7817-80, поставленного без зазора в отверстие, калиброванное разверткой, или с помощью болта (рис. 3.5 а), винта (рис. 3.5 б) или шпильки (рис. 3.5 в), поставленных в отверстия присоединяемой детали с зазором.

3.2.1. Болты, установленные без зазора (см. рис. 3.4)

В расчете полагают, что фланцы соединяемых деталей весьма жесткие и можно пренебречь их деформациями в плоскостях, параллельных плоскости стыка.

Несдвигаемость обеспечивается за счет сопротивления:

а) срезу стержня болта, б) смятию боковой поверхности болта и соединяемых деталей.

Расчет ведут полагая, что силы F_i^F , приходящиеся на болты от действия центральных внешних сил (см. рис. 3.3), одинаковы

F_i ^F = F₁ ^F =F/z ,

где z = число болтов.

Силы, нагружающие болты из-за действия момента Т, пропорцианальны расстояниям p_i от болтов до центра масс. Более нагружены наиболее удаленные, на которые действует сила F₁^Т.

F₁^T = T * 10³ * ρ_max / ∑ ρ_i²

где р_max – расстояние до наиболее удаленного болта.

Расчет ведут в такой последовательности:

1.  Определяют силы, приходящиеся на болты от действия отдельных силовых факторов;

2.  Для наиболее нагруженного болта геометрическим сложением находят суммарную действующую силу F_{1 max} ^∑ (см. рис. 3.3; 3.12; п. 3.7);

3.  Из расчета болта на срез определяют необходимый диаметр гладкой части болта (проектный расчет) или проверяют пригодность заданного диаметра (проверочный расчет) (см. рис 3.4);

4.  Полученное значение диаметра стержня d_c округляют до стандартного (ГОСТ 7817-80);

5.  Рассчитывают длину болта: а) полную, l , б) нарезанной части, (l – l₂), в) минимальную, сопротивляющуюся смятию, h_см ;

6.  Правильность принятых размеров проверяют расчетом на смятие.

Напряжение смятия σ_см условно считают равномерно распределенными по площади, являющейся проекцией поверхности смятия на плоскость, перпендикулярную действующей силе (см. далее п. 3.7).

3.2.2. Болты, установленые с зазором

Если от расчета не требуется повышенная точность, то приближенно полагают, что нагрузка в стыке локализуется в непосредственной близости от отверстий под болты (исключения оговорены ниже). Силу F_{1 max} ^∑ , действующую на наиболее нагруженный болт, определяют так же, как и для болта, поставленного без зазора.

Условие отсутствия сдвига (несдвигаемости) имеет вид

F_1тр = к_сц * F_{1 max} ^∑ , (3.1)

где F_1тр – сила трения, созданная при затяжке одного болта (винта, шпильки); к_сц – коэффициент запаса сцепления (запаса по несдвигаемости), принимают к_сц ≥ 1.5.

В свою очередь,

F_1тр =F_зат * f * i , (3.2)

где F_зат - сила затяжки одного болта; f –коэффициент трения на стыке (см. далее табл. 3.5); i – число рабочих стыков.

При нагружении соединения только центральной сдвигающей силой F условие отсутствия сдвига может быть записано в более простой форме:

F_тр =F_зат * f * i * z = к_сц * F , (3.1’)

где F_тр – суммарная сила трения на стыке деталей.

При нагружении соединения только сдвигающим моментом Т условие отсутствия сдвига имеет вид

Т_тр = к_сц * Т * 10 ³ , (3.1’’)

где Т_тр – суммарный момент сил трения на стыке деталей.

Силы трения в стыке с некоторым приближением относят к осям болтов во всех случаях за исключением тех, когда одна из стыкующихся деталей обладает большой податливостью или когда болты расположены вне стыка деталей. Пример такой конструкции показан на рис. 3.6, где средний диаметр трения (стыка)

D_тр.ср = D₁ + D₂ / 2

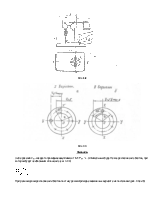
При необходимости получения высокой точности расчета, а также для стыков иных форм см. работы [1, 2, 3].

Из условий (3.1) и (3.2) находят необходимую силу затяжки каждого из болтов.

На болт (винт, шпильку) внешняя нагрузка не передается. Необходимую площадь А₁ поперечного сечения болта по диаметру d₁ и необходимый диаметр d₁ (а по нему и номинальный диаметр резьбы d) при проектном расчете определяют из условий прочности стержня болта при затяжке с силой F_зат

σ = 1,3 * F_зат / A₁ = 1,3 * F_зат / (π * d₁² / 4)

где [σ]_р – допускаемое напряжение растяжения стержня болта (см. далее табл. 3.3 и п. 3.6).

При затягивании в стержне болта за счет трения в резьбе возникают касательные напряжения кручения, что учитывают введением коэффициента перед силой F_зат в зависимости (3.3). для стандартных крепежных деталей при средних условиях трения в резьбе этот коэффициент равен 1.3.

3.3. групповое резьбовое соединение, нагруженное в плоскости,

перпендикулярной стыку

Пример соединения приведен на рис. 3.7, где С – центр масс сечений болтов. При расчете полагают, что центральная внешняя сила нагружает болты равномерно, а момент – пропорцианально их расстояниям до нейтральной, центральной оси. Наиболее нагруженным будет один или несколько наиболее удаленных болтов с раскрывающей стороны стыка.

В общем случае нужно обеспечить: 1) нераскрытие стыка, 2) прочность болтов, 3) прочность основания (для неметаллического основания).

В общей форме условие нераскрытия стыка может быть записано так:

σ_{min ст} > 0 , (3.4)

где σ_{min ст} - минимальное напряжение сжатияв стыке после приложения внешней нагрузки.

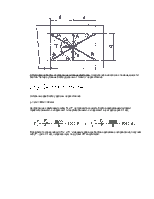
Для обеспечения выполнения условия (3.4) вводят коэффициент запаса по нераскрытию стыка к. принимают к = 1.3…1.5 (к = 1.1 – для малоответственных соединений).

Из условий (3.4), определяют необходимую для предотврещения раскрытия стыка силу F _зат каждого болта (винта, шпильки).

Внешние нагрузки (M,F) распределяются между резьбовыми деталями и стыком. на резьбовые детали действует часть нагрузки, обозначаемая χ и называемая коэффициентом основной нагрузки.

Если от расчета не требуется повышенная точность, приниимают χ = 0.2 … 0.3 – для металлических стыков и χ = 0.7 … 0.8 – для стыка металла с бетоном (в других случаях см. [1, 2, 3]).

Условие нераскрытия стыка (3.4), выраженное через напряжение на стыке, принимает вид:

σ_{min ст} = σ_зат ± σ_Fn - σ_M > 0 (3.4’)

Напряжение сжатия σ_зат на стыке от затяжки болтов (винтов или шпилек):

σ_зат = F_зат * z / A_ст

где z - число болтов на стыке; А_ст - номинальная площадь стыка (без учета наличия отверстий под болты).

Напряжениеσ_Fn на стыке от действия внешней, нормальной к стыку силы:

σ_Fn = F_N (1 - χ) / А_ст

Знаки передσ_Fn в формулах: “-” - при раскрывающей стык нагрузке, “+” - в том случае, когда нагрузка увеличивает напряжения сжатия на стыке.

Максимальное напряжение σ_M на стыке от опрокидывающего момента:

σ_M = M (1 - χ) / W_ст

где W_ст - момент сопротивления стыка относительно нейтральной оси.

Если нейтральная ось обозначена х-х, то

W_{X ст} = I_{x ст} / y_{max ст}

где I_{x ст} - момент инерции стыда относительно нейтральной оси; y_{max ст} - расстояние от нейтральной оси до наиболее удаленных точек стыка с разгружаемой стороны стыка.

После введения коэффициента запаса по нераскрытию к и преобразований, условие нераскрытия стыка принимает вид:

Откуда видно, что при одинаковом для стыков разных форм значении y_{max ст} наиболее рациональным будет тот стык, у которого имеет максимальное значение отношение = I_{x ст} / А_ст.. При этом будет минимальным значение необходимой силы F_зат по условию нераскрытия стыка.

Необходимую площадь поперечного сечения болта А₁ (проектный расчет) находят из условия прочности болта

где коэффициент 1, 3 учитывает скручивание болта при его затяжке; F_зат - суммарная внешняя растягивающая нагрузка, приходящаяся на наиболее нагруженный болт; А₁ - площадь болта по диаметру d₁ (см. п. 3.1)

A₁ = p * d₁² / 4

[σ]_р - допускаемое напряжение растяжения для болта (см. далее п. 3.6).

В свою очередь,

где W_{x всех болтов} - момент сопротивлениявсех болтов относительно нейтральной оси х.

Пренебрегая моментом сопротивления болта относительно собственной центральной оси, можно записать

где у_{i Б} - расстояние от нейтральной оси до некоторого i - го болта; у _{max Б} - то же для наиболее удаленного болта, находящегося на раскрываемой стороне стыка. Пример оптимизации расположения болтов по стыку приведен в п. 3.5.

Неметаллическое основание проверяют по условию прочности на смятие

s _{max ст} < [s ]_см

гдеσ_{max ст} максимальное напряжение сжатияна стыке после приложения внешней нагрузки (см. рис. 3.7); [σ]_см - допускаемое напряжение смятия (см. далее табл. 3.4).

3.4. Групповое резьбовое соединение, нагруженное в плоскости стыка

и в плоскости, перпендикулярной стыку

Необходимо обеспечить: I) нераскрытие стыка (3.4); 2) несдвигаемость (3.1); 3) прочность болтов (3.5); 4) прочность основания (3.6), если оно неметаллическое.

Расчет болтов на прочность ведут по большей из двух сил затяжки, найденных из условия нераскрытия и несдвигаемости (см. далее п. 3.8).

3.5. Пример выбора оптимального варианта расположения болтов

на кольцевом стыке

Стойку 1 (рис. 3.8 и 3.9) настольного сверлильного станка с помощью фланца 2 крепят шестью болтами 3 к основанию 4. На сверло действует сила резания F_рез. Определить оптимальный вариант расположения болтов на радиусе R стыка.

Рис. 3.8

Рис. 3.9

Решение.

Сила резания F_рез создает опрокидывающий момент М = F_рез * L. Оптимальным будет такое расположение болтов, при котором будет наибольшим отношение (см. п. 3.3)

При равномерном расположении болтов по стыку рассмотрим два возможных вариантаих постановки (рис. 3.9а и б)

В варианте 1 два болта имеют максимальное расстояние до оси x: y_1Б = y_maxБ = R , у остальных четырех болтов расстояние y_2Б = R * sin30⁰ = 0,5 * R. Тогда

В варианте 2 четыре болта удалены от нейтральной оси на максимальное расстояние y = R * sin60⁰ = 0,867 R , у двух остальных y_2Б = 0. Следовательно,

Вывод: оптимальным является вариант 2.

3.6. Допускаемые напряжения при статической нагрузке

Допускаемые напряжения [σ]_p для расчета болтов на растяжение:

[σ]_p = σ_T / S_T

где σ_T предел текучести материала болта (см. табл. 3.2); S_T коэффициент запаса прочности.

Для ответственных резьбовых соединений силу затяжки контролируют. В этом случае S_T = 1, 2...1, 5. Значения S_T при неконтролируемой затяжке приведены в табл.3.3.

Табл. 3.3

Значения коэффициента запаса s_T при расчете болтов (винтов, шпилек) с неконтролируемой затяжкой

Табл. 3.4

Допускаемые напряжения для расчета на срез и смятие

Табл. 3.5

Значения коэффициента трения f

3.7. Пример расчета группового резьбового соединения, нагруженного в плоскости стыка

Блок I натяжного устройства (рис. 3.10) нагружен силой F_Q = 12000 Н, созданной массой груза, и силой натяжения горизонтального каната F_K = 12000 Н. Опоры оси блока размещены в корпусах 2. Каждый из корпусов прикреплен двумя болтами 3 к кронштейнам 4. Кронштейны крепятся к колонне 6 болтами 5. Число болтов крепления каждого кронштейна z = 6. Класс прочности болтов 5.8, они поставлены c зазором. Кронштейны 4 и колонна 6 изготовлены из горячекатаной стали Ст3. Размеры деталей: l₁ = 200 мм; l₂ = 400 мм; d_б = 200 мм; a = 80 мм; b = 80 мм; s₁ = s ₂ = 10 мм.

Требуется определить диаметр болтов 5.

Решение

1.  Положение центра масс болтов 5. Центр масс болтов 5 находится в точке С, на пересечении осей симметрии соединения.

2. Перенос нагрузки в центр масс - точку С. Нагрузка от блока распределяется между двумя кронштейнами 4. Можно рассмотреть соединение одного кронштейна с колонной, нагруженное половиной внешней нагрузки. При переносе сил F_Q/2 и F_K/2 в точку С (рис. 3.11) получаем следующие силовые факторы:

F_В = F_Q /2 = 12000/2 = 6000 Н.

вертикальную сдвигающую силу

F_Г = F_K /2 = 12000/2 = 6000 Н.

горизонтальную сдвигающую силу

сдвигающий момент

3. Нагрузка на болты от отдельных силовых факторов. Соединение выполнено с помощью шести болтов. Четыре угловых болта удалены от точки С на расстояние

Остальные два болта удалены на расстояние

ρ = a/2 = 80/2 = 40 мм.

Центральные сдвигающие силы F_В и F_Г нагружают все шесть болтов одинаковыми силами горизонтальными - с индексом 1г и вертикальными - с индексом 1в (см. далее рис.3.12а);

В результате сложения сил F_1В^F и F_1Г^F имеющих для всех болтов одинаковое направление, получим силу F₁^F (рис. 3.12а), направленную под углом 45° к вертикали:

Нагрузка на болты от момента пропорциональна их расстояниям до центра масс. На угловые болты будет действовать сила

Болты, удаленные от центра масс на расстояние ρ₂, нагружены меньшей силой F₂^F от действия момента.

4. Нагрузка, приходящаяся на наиболее нагруженный болт. Наиболее нагруженным будет тот из угловых болтов, для которого составляющие силы, действующие на него, наиболее близки по направлению. К силе F₁^F наиболее близка по направлению сила F₁^Т, действующая на болт Е (рис. 5.12б). Эта сила образует о вертикальной угол α:

Суммарная сила, действующая на болт

5. Необходимая сила затяжки из условия несдвигаемости (3.1). Сдвига не будет, если

F_1ТР = к_СЦ* F_1MAX^∑

где F_1MAX^∑ - суммарная сдвигающая сила, приходящаяся на наиболее нагруженный болт, F_1MAX^∑ = 10498, 75 Н; к_СЦ - коэффициент запаса сцепления (запаса по несдвигаемости) к_СЦ = 1, 5;

F_1ТР - сила трения, созданная при затяжке одного болта (3.2):

F_1ТР = F_ЗАТ * f * i

здесь f коэффициент трения. Принимаем f = 0,2 (см. табл. 3.5); i - число рабочих стыков (по условию i = 1). Тогда

6. Необходимый диаметр болта из условия прочности затянутого болта (3.3)

где [σ]_Р - допускаемое напряжение растяжения болта.

Затяжку болтов не контролируют. Предполагаем, что диаметр болта d больше 16 мм. Принимая коэффициент запаса s_Т = 2, 5 (cм. табл. 3.3), получаем

[σ]_Р = σ_Т / s_Т = 400 / 2.5 =160 Мпа,

где σ_Т = 400 МПа - предел текучести болтов класса прочности 5.8 (см. табл. 3.2). В результате

Пригодны болты М36, у них d₁ = 31, 67 мм (см. табл. 3.1) Предположение о том, что d > 16 мм подтвердилось.

Примечание. Решим предыдущий пример при постановке болтов 5 без зазора. Конструкция болта показана на рис. 3.4. Опасными для соединения являются напряжения среза для болта и смятия для болта и стенок отверстия.

Условие прочности болта на срез

откуда

В соответствии с табл. 3.4 [τ]_СР = (0,2…0,3)σ_Т. Принимаем [τ]_{СР =} 0,25*σ_Т. Согласно табл. 3.2 для класса прочности 5.8, σ_Т = 400 МПа. Тогда

Принимаем по ГОСТ 7817-80 [4] болты М12, у которых d_С = 13 мм. Необходимая длина болта l’ (см. рис. 3.4):

l’ = s₁ + s₂ + s + H + (0,4…0,6)*d

По ГОСТ 6402-70 [4] толщина пружинной легкой шайбы s = 2, 5 мм; по ГОСТ 5915-70 [4] высота гайки Н = 10 мм; (0, 4...0, 6) * d - запас резьбы над гайкой и высота пяты (ориентировочно)

l’ = 10 + 10 + 2.5 + 10 + (0,4 … 0,6) * 12 = 37,3…39,7 мм.

Принимаем по ГОСТ 7817-80 l = 40 мм, тогда l – l₂ = 22 мм; фаска f = 0, 5 мм.

Высота поверхности h_СМ на которой действуют наибольшие напряжения смятия σ_СМ2:

h_СМ = l – (l – l₂) – f – s₁ = 40 – 22 – 0,5 –10 = 7,5

Проверяем соединение на предотвращение смятия по условию

где А_СМ - площадь проекции поверхности смятия; [σ]_СМ допускаемое напряжение смятия.

Согласно табл. 3.4 [σ]_СМ = (0, 35... 0,45) принимаем [σ]_СМ = 0,4. Для болтов σ_Т = 400 МПа, для материала кронштейна (сталь СтЗ) σ_Т = 220 МПа (см. табл. 1.2).

Расчет ведем по наименее прочному материалу:

[σ]_СМ = 0,4 * 220 = 88 МПа, σ_СМ = 10498,75 / (7,5 *13) = 107,68 МПа.

Условие прочности не выполняется для материала кронштейна, но выполняется для болтов, у которых [σ]_СМ = 0,4*400 = 160 МПа.

Меняем материал кронштейна на более прочный. Назначаем сталь Ст6 у которой σ_T = 300 МПа. [σ]_СМ = 0,4* 300= 120 МПа.

Если материал кронштейна по каким-либо причинам нельзя изменить, необходимо увеличить толщину листов кронштейна.

После расчета можно определить, что требуемая толщина s₁ = s₂ = 12 мм. При этом длина болта l = 45 мм, а l – l₂ = 22 мм.

Следует отметить, что при постановке болтов без зазора их диаметр существенно уменьшается (М12 вместо М36).

3.8. Пример расчета группового резьбового соединения. нагруженного в плоскости стыка и в плоскости. перпендикулярной стыку

Исходные данные приведены в разделе 2.7, конструкция показана на рис. 2.3. Требуется определить диаметр болтов 3.

Решение

I. Положение центра масс и действующие на соединение силовые факторы. Соединение имеет две оси симметрии, центр масс находится на их пересечении в точке О (рис. 3.13). При параллельном переносе внешней силы F в точку О (рис. 3.14) получаем действующую на соединение центральную сдвигавшую силу F = 10000 Н и отрывающий момент М = F * L = 10000*200 = 2*10⁶ Н*мм.

рис. 3.13.

рис. 3.14.

2.  Необходимая сила затяжки болта F’_ЗАТ из условия несдвигаемости (3.1):

F_ТР = к_СЦ * F

где F_ТР - сила трения на стыке; к_СЦ - коэффициент запаса сцепления (запаса по несдвигаемости), к_СЦ > 1,5; F - центральная внешняя cдвигающая сила.

(Момент М₁ перераспределяет давление на стыке, не меняя значение силы трения.) В свою очередь,

F_ТР = F’_ЗАТ * z * f * i

где z - число болтов, z = 4; f - коэффициент трения, f = 0,4 для стыка металл - бетон (см. табл. 3.5); i - число рабочих стыков, по условию i = 1. Тогда

F'_зат = к_сц * F / (к * f * i) = 1,5*10000 / (4*0,4*1*)= 9375 Н

3. Необходимая сила затяжки болта F”_ЗАТ из условия (3.4) нераскрытия стыка (см. рис. 3.14, эпюры напряжение)

σ_{min СТ} > 0,

где минимальное напряжение сжатия на стыке после приложения внешней нагрузки.

В свою очередь σ_{min СТ} = σ_ЗАТ – σ_М

3десь σ_ЗАТ = F”_ЗАТ * z / A_CT напряжение на стыке от затяжки болтов; A_CT - площадь стыка (без учета отверстий под болты); σ_М = M₁ * (1 - χ) / W_{X CT} - напряжение на стыке от действия момента; χ - коэффициент основной нагрузки;

W_{X CT} = I_{X CT} / y_{MAX CT} момент сопротивления стыка относительно нейтральной оси х-х; в нашем случае W_{X CT} = a * b² / 6 .

Вводя коэффициент запаса к по нераскрытию стыка, получаем

F"_зат = к * M * (1-x)* A_ст / (W_xст * z)

Принимаем к = 1, 3, - 0, 75 (стык: металл - бетон). Тогда

F"_зат = 1,3 * 2*10000 * (1-0,75)* 200 * 200 * 6 / (200 * 40000*4) = 4875 H

4. Принимаем силу затяжки болта F_ЗАТ = 9375 Н. (большую из двух необходимых).

5. Условие прочности болта (3.5) принимает вид

где А₁ - площадь болта по диаметру d₁ (см. п. 3.1); F_{∑ ВН} - суммарная внешняя растягивающая нагрузка, приходящаяся на один болт.

Силы. приходящиеся на болты от действия момента, пропорциональны расстояниям у_{i б} - от болтов до нейтральной линии.

Максимально нагружены наиболее удаленные от нейтральной линии на расстояние у_{MAX Б} болты, дополнительно растягиваемые при действии момента. В нашем случае

6. Необходимый диаметр болта. Необходимая площадь А₁:

где [σ]_P = σ_T / s_T - допускаемое напряжение для расчета болтов на растяжение; - σ_T - предел текучести материала болта; s_T - коэффициент запаса прочности.

Предполагаем, что диаметр болта d менее 30 мм, принимаем s_T = 4 (см. табл. 3.3).

Для болтов класса прочности 4.6 σ_T = 240 МПа (см. табл. 3.2). Тогда

7. Заключение по результатам расчета болтов; пригоден болт М24, у него d₁ = 20, 75 мм (см. табл. 3.1). Предположение о том, что d<30 мм, подтвердилось.

1.  Проверка прочности бетонного основания:

σ_{max CT} = σ_ЗАТ + σ_М ≤ [σ]_CM

где σ_{max CT} - максимальное напряжение на стыке; [σ]_CM - допустимое для бетона напряжение смятия, [σ]_CM = 1, 8 МПа (см. табл. 3.4). Тогда

Основание достаточно прочное.

Примечание. Рассмотрим вариант расчета болтов крепления кронштейна к бетонной стене (см. рис. 2.3) в том случае, когда требуется определить класс прочности болтов при известных ограничениях на их диаметр (назначаемых из условий размещения болтов и возможности затяжки их стандартным накидным ключом).

Решим пример при условии, что диаметр болтов d должен удовлетворять условию:

Решение.

1. Максимально возможный диаметр болта.

2. Назначаем болты М16, у которых диаметр d₁ = 13,835 мм (см. табл. 3.1).

3. Используем приведенные выше в решении зависимости

Назначаем коэффициент запаса прочности болта s_T = 4 (см. табл. 3.3), тогда пригодными будут болты, имеющие предел текучести материала σ_T:

Пригодны болты класса прочности 6.8 (см. табл. 3.2, σ_T = 480МПа).