Идентификация модели поляризованного преобразователя импульсного расхода жидкости методом многофакторного эксперимента
|
Уровни факторов |
Факторы процесса |
||
|
X1 |
X2 |
X3 |
|
|
Нижний |
23 |
120 |
5 |
|
Основной |
34 |
136 |
8 |
|
Верхний |
45 |
152 |
11 |
|
Интервал варьирования |
11 |
16 |
3 |
|
Массив данных |
|||
|
Y1 |
Y2 |
Y3 |
Y4 |
|
0,12 |
0,12 |
0,11 |
0,12 |
|
0,08 |
0,06 |
0,07 |
0,08 |
|
0,20 |
0,18 |
0,21 |
0,20 |
|
0,18 |
0,17 |
0,18 |
0,17 |
|
0,13 |
0,12 |
0,14 |
0,16 |
|
0,11 |
0,12 |
0,11 |
0,10 |
|
0,22 |
0,23 |
0,22 |
0,21 |
|
0,20 |
0,21 |
0,20 |
0,18 |
N=2k=23=8
|
№ опыта |
X1 |
X2 |
X3 |
Y1 |
Y2 |
Y3 |
Y4 |
|
|
|
1 |
-1 |
-1 |
-1 |
0,12 |
0,12 |
0,11 |
0,12 |
0,1175 |
0,0000703 |
|
2 |
-1 |
-1 |
+1 |
0,08 |
0,06 |
0,07 |
0,08 |
0,0725 |
0,000232 |
|
3 |
-1 |
+1 |
-1 |
0,20 |
0,18 |
0,21 |
0,20 |
0,1975 |
0,00047 |
|
4 |
-1 |
+1 |
+1 |
0,18 |
0,17 |
0,18 |
0,17 |
0,175 |
0,0000812 |
|
5 |
+1 |
-1 |
-1 |
0,13 |
0,12 |
0,14 |
0,16 |
0,1375 |
0,000495 |
|
6 |
+1 |
-1 |
+1 |
0,11 |
0,12 |
0,11 |
0,10 |
0,11 |
0,000125 |
|
7 |
+1 |
+1 |
-1 |
0,22 |
0,23 |
0,22 |
0,21 |
0,22 |
0,000125 |
|
8 |
+1 |
+1 |
+1 |
0,20 |
0,21 |
0,20 |
0,18 |
0,1975 |
0,000245 |
|
0,1975 |
0,00023 |
Построение линейной модели
![]()
Проверка на однородность по критерию Фишера:
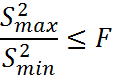
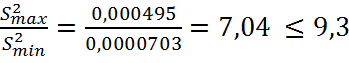 это означает, что
дисперсии однородны.
это означает, что
дисперсии однородны.
Оценка адекватности
Дисперсия адекватности:
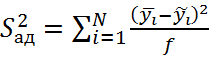
![]()
![]() получаем
в результате подстановки соответствующих величин факторов
получаем
в результате подстановки соответствующих величин факторов ![]() в математическую модель.
в математическую модель.
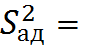 0,0000476
0,0000476
|
|
|
0,111 |
|
0,082 |
|
0,199 |
|
0,17 |
|
0,137 |
|
0,108 |
|
0,196 |
Проверку на адекватность производят с использованием F-критерия Фишера:
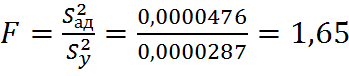 , где
, где
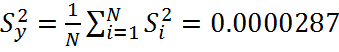
Fтабл>F -условие адекватности
4,5>1,65 - полученная модель адекватна.
Проверка значимости
Проверку производят с помощью критерия Стьюдента ,
эмпирическое значение которого 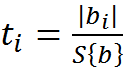 , где
, где
![]() - дисперсия оценки b
коэффициента уравнения регрессии.
- дисперсия оценки b
коэффициента уравнения регрессии.
|
|
|
|
|
|
|
|
28,6 |
2,39 |
8,22 |
-2,72 |
Табличное
значение коэффициента Стьюдента t=2.06, поэтому значимыми признаются все
оценки коэффициентов уравнения регрессии.
Доверительный интервал:
![]()
Движение по градиенту
Составляющие градиента однозначно получаются умножением коэффициентов регрессии на интервал варьирования по каждому фактору.
Расчет мысленных опытов
|
Мысленные опыты |
x1 |
x2 |
x3 |
|||||||||
|
Коэффициенты bi |
0,01281 |
0,04406 |
-0,0147 |
y (кр.в.) |
||||||||
|
Шаг (bi*Ji) |
0,14094 |
0,705 |
-0,0441 |
|||||||||
|
Опыт 9 |
11,1409 |
16,705 |
2,95594 |
|||||||||
|
Опыт 10 |
11,2819 |
17,41 |
2,91188 |
|||||||||
|
Опыт 11 |
11,4228 |
18,115 |
2,86781 |
|||||||||
|
Опыт 12 |
11,5638 |
18,82 |
2,82375 |
|||||||||
|
Опыт 13 |
11,7047 |
19,525 |
2,77969 |
|||||||||
|
Опыт 14 |
11,8456 |
20,23 |
2,73563 |
|||||||||
|
Опыт 15 |
11,9866 |
20,935 |
2,69156 |
|||||||||
|
Опыт 16 |
12,1275 |
21,64 |
2,6475 |
|||||||||
|
x1 |
x2 |
x3 |
y (кр.в.) |
|||
|
Опыт 9 |
0,14094 |
0,705 |
-0,0441 |
0,18695 |
||
|
Опыт 10 |
0,28188 |
1,41 |
-0,0881 |
0,22047 |
||
|
Опыт 11 |
0,42281 |
2,115 |
-0,1322 |
0,25399 |
||
|
Опыт 12 |
0,56375 |
2,82 |
-0,1763 |
0,28751 |
||
|
Опыт 13 |
0,70469 |
3,525 |
-0,2203 |
0,32102 |
||
|
Опыт 14 |
0,84563 |
4,23 |
-0,2644 |
0,35454 |
||
|
Опыт 15 |
0,98656 |
4,935 |
-0,3084 |
0,38806 |
||
|
Опыт 16 |
1,1275 |
5,64 |
-0,3525 |
0,42157 |
||
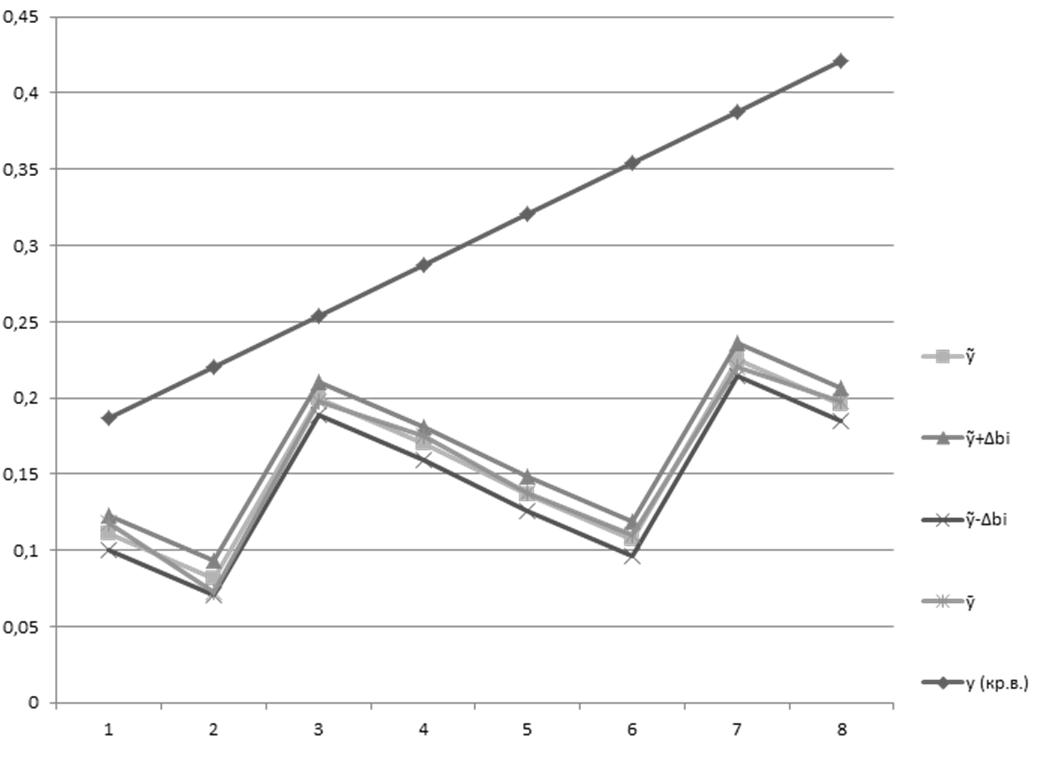
Вывод: Реализация мысленных опытов на стадии крутого восхождения привела к улучшению значения параметра оптимизации по сравнению с самым хорошим параметром планирования эксперимента.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.