Расчёты формулы обращения

Формула обращения

Обратное дискретное преобразование Лапласа определяет функцию  по заданному изображению и определяется по формуле:

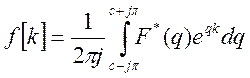, при    (1)

Здесь , где - абсцисса абсолютной сходимости.

Для смещенной дискретной функции имеем:

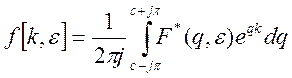   (2)

Для Z-преобразования имеем формулу:

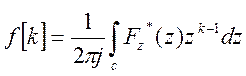  (3)

Здесь интегрирование производится по окружности С радиуса . При этом контур обходится в положительном направлении.

Обратное дискретное преобразование и Z-преобразование будем обозначать: и .

Принимая во внимание, что функция является неаналитической в окружности C принимается теорема о вычетах:

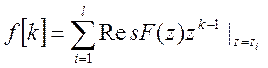  (4)

Где - полюс функции , лежащей внутри окружности.

Вычет функции в простом полюсе определяется формулой:

   (5)

Вычет функции в полюсе высших порядков определяется формулой:

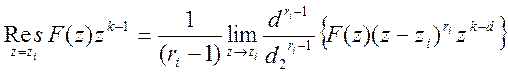   (6)