Расчет электронных схем, страница 5

3. Строят графики частотной зависимости квадрата АЧХ и затухания.

4. Квадрат АЧХ записывают в операторной форме путем замены оператора  на оператор Р

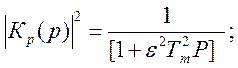           (9. 13)

5. Записывают полином и находят полюсы (Р_к)

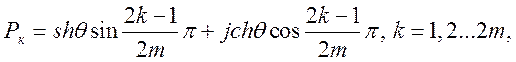
где      .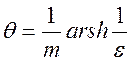

Из корней составляют сомножители (р-р_i) и строят передаточную функцию

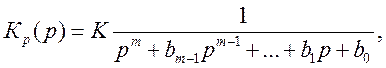         (9. 14)

где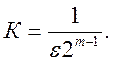     

Далее расчет осуществляется по методике расчета фильтра Баттерворта.

9. 12. Расчет активных RC-фильтров.

Исходными данными для расчета являются:

1.  граничная частота фильтра ;

2.  тип и порядок фильтра (Баттерворта, Чебышева, Бесселя);

3.  коэффициент усилителя.

На основании исходных данных выполняется расчет в следующей последовательности:

1. Определяют необходимое количество звеньев первого и второго порядка и изображают схему. Например, требуется рассчитать параметры фильтра Баттерворта 5-го порядка. Такой фильтр можно создать, соединив между собой одно звено первого порядка.

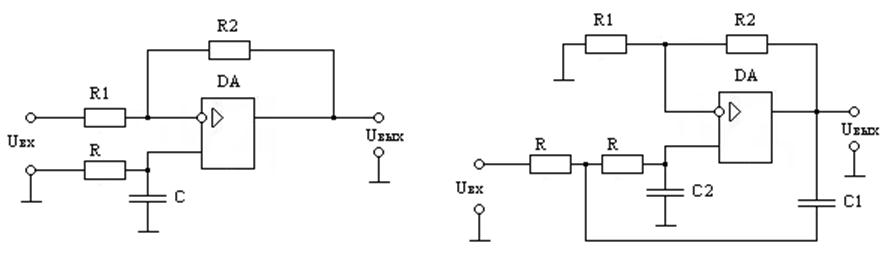
Рис 9. 28. Активные RC-фильтры первого порядка-(а) и второго порядка-(б)

2. Рассчитывают параметры RC- цепи для всех звеньев фильтра из условия               .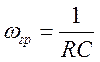

Задают, например,  тогда             

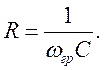
3.  Рассчитывают коэффициенты усиления второго каскада, используя приведенные в таблице 3 полиномы знаменателя для передаточной характеристики фильтра Баттерворта.

Таблица 3

Порядок фильтра(n)	Полином знаменателя
1	(р+1)
2	(р2+1,414р+1)
3	(р+1) (р2+р+1)
4	(р2+0,765р+1) (р2+1,848р+1)
5	(р+1) (р2+0,618р+1) (р2+1,618р+1)

Для звена второго порядка коэффициент передачи определяется выражением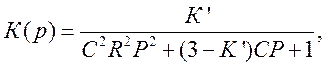                      

где- коэффициент усиления операционного усилителя.

Чтобы АЧХ операционного усилителя повторяла АЧХ фильтра Баттерворта необходимо приравнять множители полиномов при операторе . Для фильтра Баттерворта пятого порядка необходимо приравнять множитель второго члена знаменателя  множителя второго члена Р во вторых скобках пятой строки таблицы 3   Из этого равенства определяют .

4.  Зная 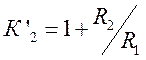 определяют .

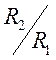5. Чтоб обеспечить симметрию входных цепей операционного усилителя по постоянному току для исключения смещения нуля необходимо выполнить условие

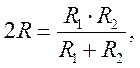 откуда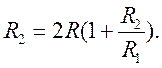

Зная  и отношение , определенное в пункте 4, находят

6. Для третьего звена фильтра приравнивают множитель второго члена знаменателя К(Р) к множителю второго члена при операторе Р в третьих скобках пятой строки табл. 3.

Определяют .

7. Зная 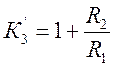 определяют для третьего звена фильтра.

8. Исходя из условия симметрии входных цепей третьего звена фильтра определяют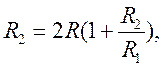                 

тогда из отношения  определяют .

9. Определяют коэффициент усиления второго и третьего звеньев фильтра

10. Исходя из условий решаемой задачи находят потребный коэффициент усиления первого звена. Например, если необходимо иметь общий коэффициент усиления трехзвенного фильтра равным К, то усиление первого звена будет

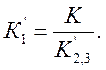
11. Зная , определяют , тогда       

12. На основании  отношения              определяют      .

13. Если RC- цепи, параметры которых определены в пункте 2, включить по схеме интегрирующих цепей, то получаем фильтр нижних частот, а если они включены по схеме дифференцирующих цепей, то – фильтр верхних частот.

14. Полосовой фильтр можно получить последовательным включением звеньев нижних и верхних частот. В этом случае частота среза фильтра нижних частот выше частоты среза верхних частот.

15. Режекторный фильтр можно получить путем параллельного включения входов и выходов звеньев нижних и верхних частот.

Пример.Используя ОУ, спроектировать активный фильтр высокой частоты с коэффициентом передачи Кu и нижней частотой полосы пропускания f_н , при известной Т_оу.

1.  Нижняя круговая частота полосы пропускания

2.  Коэффициент передачи цепи ООС на высокой частоте

b_oc=R_oc2/(R_oc1+ R_oc2)=(K_U0 - K_U)/( K_U0K_U  ).

3.       Для цепи ООС имеем Т_ч1<T_ч2, однако K_U0>>1 и можно считать

Т_оос≈ Т_ч1= R_oc2 С_oc.

Принимаем  R_oc=2,4 кОм, тогда

4.  Определим сопротивление резистора R_oc1:

K_U=1+ R_oc1/ R_oc2   или  R_oc1=(K_U -1) R_oc2;

5.  ЛАЧХ идеального фильтра высокой частоты после ω=ω_H  должна иметь постоянный коэффициент передачи до частоты ω=∞. Фильтр на рис.9. 29  является не фильтром высокой частоты, а полосовым фильтром.  В рассматриваемом случае

Т_в=Т_ОУ/(1+ K_U0b_oc).

f_B=1/2π Т_в.

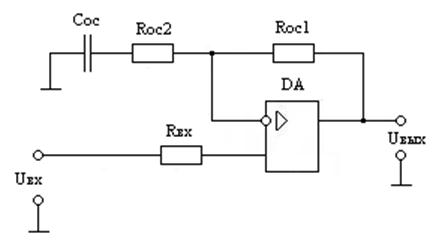
Рис.9. 29  Схема фильтра высоких частот.

Схемой полосового фильтра является схема дифференциатора с цепями коррекции (рис. 9. 30). При выборе R_kC≠C_kR, в ЛАЧХ данной схемы появляется участок с нулевым наклоном. Продолжительность этого участка и определяет полосу пропускания полосового фильтра. 

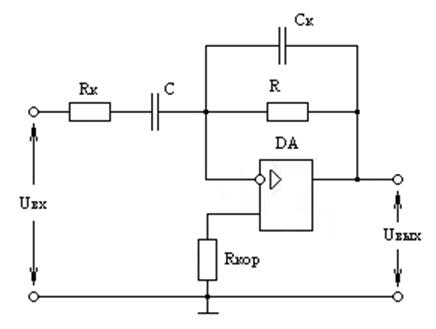
Рис.9. 30  Базовая схема дифференциатора с цепями коррекции.

9. 13. Расчет схем  сравнения.

Пример1. Используя ОУ, рассчитать схему сравнения с заданным порогом срабатывания. Погрешность срабатывания не должна превышать 0,1%.

1. Для реализации исходных требований воспользуемся схемой на рис.9.31.

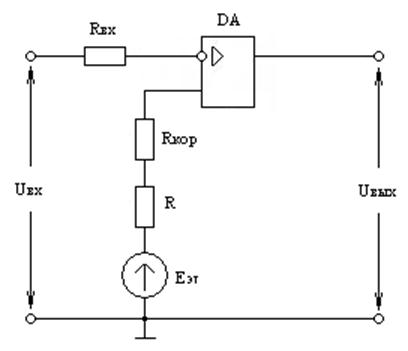
Рис.9.31. Однопороговая схема сравнения со смещенным порогом срабатывания.

2.  Диапазон изменения входного напряжения для заданного ОУ составляет

∆U_вх=2 U_{вых max}/ К_UO.

В данном случае погрешность определения уровня 0,1 составит δ=(∆U_вх/∆U_cр)100%

3.          Полученная погрешность больше заданной. Поэтому необходимо либо уменьшить напряжение, используя цепь нелинейной ООС, либо увеличить К_UO введением цепи ПОС.

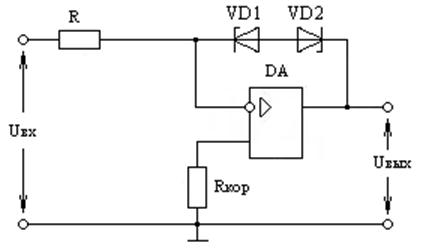
Рис.9. 32. Схема ограничителя уровня.

4.       Введём в схему цепь ПОС. Требуемый с точки зрения обеспечения заданной точности диапазон входных напряжений.                                 

2δ U_cр/100.

Необходимый для получения найденного ∆U_вх коэффициент К_{U ПОС} равен

К_{U ПОС}=2 U_{вых max}/∆U_вх.