7) Рассчитывают и строят график частотной зависимости характеристического сопротивления рассчитываемого Т- или П- звена
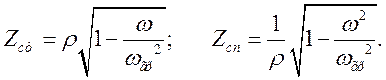
9. 9. Расчет звеньев фильтра типа m.
1.
Выполняют расчет звена прототипа,
т. е. звена типа ![]() , по методике «Расчет
звеньев фильтра типа
, по методике «Расчет
звеньев фильтра типа ![]() ».
».
2. Выбирают значение параметра m.
3. Определяют частоту бесконечного затухания.
4. Изображают схему Т- или П- звена фильтра типа m.
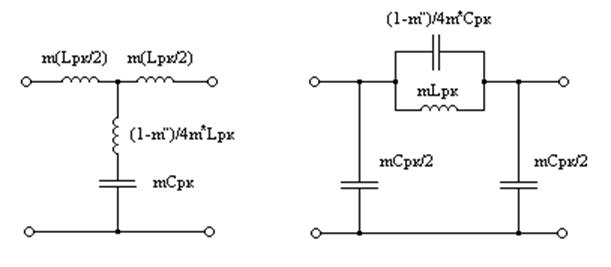
Рис. 9.24. Т-звено фильтра типа m. Рис. 9. 25. П-звено фильтра типа m.
На
рисунке 9. 24 и 9. 25 обозначено ![]() и
и ![]() - рассчитанные в пункте 1 индивидуальность
и емкость
- рассчитанные в пункте 1 индивидуальность
и емкость ![]() -звена.
-звена.
5.
Полученные в пункте 1, значения
индуктивности ![]() и емкости
и емкости ![]() звена типа
звена типа ![]() пересчитывают в индуктивность и
емкость звена типа m. Пересчитанные значения обозначают на схеме.
пересчитывают в индуктивность и
емкость звена типа m. Пересчитанные значения обозначают на схеме.
6. Рассчитывают затухание в заданной полосе частот.
7. Рассчитывают характеристическое сопротивление в заданной полосе частот.
8. Изображают и анализируют графики частотной зависимости затухания и характеристического сопротивление рассчитанного фильтра.
Пример. Рассчитаем элементы звена фильтра типа m с заданной частотой среза, отклонением характеристического сопротивления от его номинального значения для рабочей полосы частот. А также рассчитаем затухание в полосе частот, если заданно сопротивление нагрузки.
1. Выбираем m.
2.
Используя данные элементы
фильтра нижних частот типа ![]() , определим
значение элементов фильтра типа m. Выбираем П- образное последовательно- производное
звено. Элементы этого звена определяем по формулам:
, определим
значение элементов фильтра типа m. Выбираем П- образное последовательно- производное
звено. Элементы этого звена определяем по формулам:
![]()
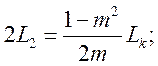
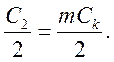
3. Для расчета затухания фильтра определим частоту бесконечного затухания:
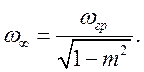
Задавшись различными значениями ![]() от 1 до 2, определим затухание
фильтра в полосе частот от
от 1 до 2, определим затухание
фильтра в полосе частот от ![]() до
до ![]() . Для этого необходимо, определить
при различных значениях
. Для этого необходимо, определить
при различных значениях ![]() значения
выражения:
значения
выражения:
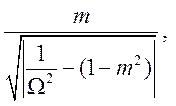
а затем по таблице ch определим
затухание в полосе от ![]() =1 до
=1 до ![]() =1,25 и по таблице sh- в
полосе от
=1,25 и по таблице sh- в
полосе от ![]() =1,25 до
=1,25 до ![]() =2.
Данные вычисления и вычисления значения затухания звена заносим в таблицу 1.
=2.
Данные вычисления и вычисления значения затухания звена заносим в таблицу 1.
Таблица 1
|
|
|
|
|
|
|
|
4. Определим характеристическое сопротивление фильтра по формуле :
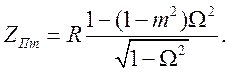
Для этого, задавшись различными значениями ![]() в полосе частот, вычислим
характеристическое сопротивление. Вычисленные значения занести в таблицу 2.
в полосе частот, вычислим
характеристическое сопротивление. Вычисленные значения занести в таблицу 2.
Таблица 2.
|
|
|
|
|
|
|
9. 10. Расчет фильтра Баттерворта.
1. Исходя из условий работы фильтра Баттерворта задают:
максимальное рабочее ослабление в полосе пропускания ![]() ;
;
минимальное рабочее ослабление в полосе задержания ![]() ;
;
граничную частоту полосы пропускания ![]() ;
;
граничную частоту полосы задержания ![]() .
.
2. Используя исходные данные определяют:
нормированную частоту полосы задержания
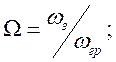
коэффициент неравновесного ослабления в полосе пропускания
![]() ;
;
порядок фильтра
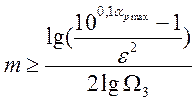
квадрат АЧХ фильтра
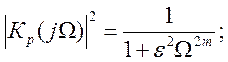 (9. 1)
(9. 1)
рабочее ослабление фильтра
![]()
строят и анализируют графики квадрата АЧХ и рабочего ослабления.
3. Находят передаточную функцию фильтра по следующей методике:
квадрат АЧХ записывают в операторном
виде, заменяя оператор ![]() на оператор
на оператор ![]()
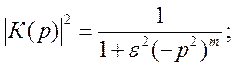 (9. 2)
(9. 2)
знаменатель полученной функции разлагают
на произведение сомножителей, для этого решают уравнение ![]() и находят корни
и находят корни
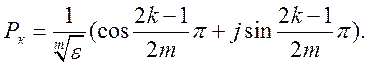 (9. 3)
(9. 3)
Вычислив корни по формуле (9.3) для четных m(p) и не четных m(-p), записывают выражение (9.2) в следующем виде
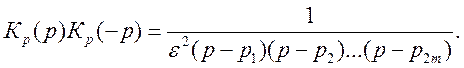 (9. 4)
(9. 4)
Учитывая, что реализуемой является только ![]() , выражение (9.4) примет
вид
, выражение (9.4) примет
вид 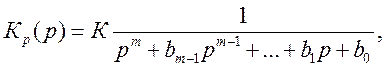
где 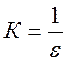 .
.
Если принять ![]() и
m=2, то выражение (9. 2) примет вид
и
m=2, то выражение (9. 2) примет вид
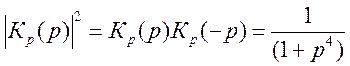
Из формулы (9. 3) имеем:
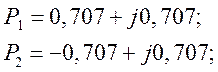
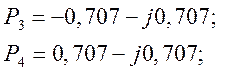
Реализуемыми являются только корни (полюса), которые
лежат в левой полуплоскости переменной ![]() ,
т. е. корни
,
т. е. корни ![]() и
и ![]() ,
следовательно выражение (9.4) примет вид
,
следовательно выражение (9.4) примет вид
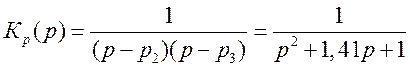 (9. 5)
(9. 5)
4. Определяют структуру и параметры элементов фильтра по следующей метке:
Пассивный LC- фильтр представляют в виде
реактивного четырехполюсника с входным сопротивлением ![]() ,
включенного между генератором с внутренним сопротивлением
,
включенного между генератором с внутренним сопротивлением ![]() и сопротивлением нагрузки
и сопротивлением нагрузки ![]() , и находят входное сопротивление
, и находят входное сопротивление
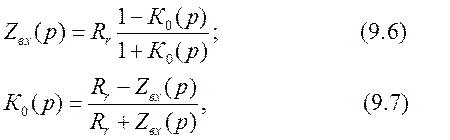
где ![]() - коэффициент
отражения на входе четырехполюсника.
- коэффициент
отражения на входе четырехполюсника.
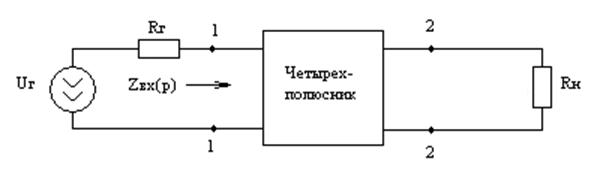
Рис. 9.26. Реактивный четырехполюсник.
Коэффициент отражения ![]() связан
с передаточной функцией
связан
с передаточной функцией ![]() соотношением
соотношением
![]() (9. 8)
(9. 8)
Учитывая (9. 5), выражение (9. 8) примет вид
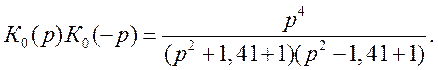
Нули этой функции равны нулю (Р01=Р02 =Р03=Р04=0), тогда полином числителя (Р-Р01)(Р-Р02)=Р2 , откуда
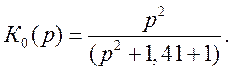 (9.
9)
(9.
9)
Подставим
![]() в виде проводимости
в виде проводимости 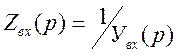 и проводят разложение проводимости в
цепную (лестничную) дробь по методу Кауэра (разложение в цепную дробь
осуществляется последовательно делению полинома знаменателя на полином
числителя, последнего- на остаток от первого деления, остатка от первого
деления- на остаток от второго деления и т. д. ).
и проводят разложение проводимости в
цепную (лестничную) дробь по методу Кауэра (разложение в цепную дробь
осуществляется последовательно делению полинома знаменателя на полином
числителя, последнего- на остаток от первого деления, остатка от первого
деления- на остаток от второго деления и т. д. ).
Выполнив разложения получим
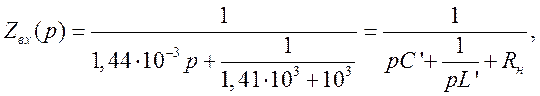
где
![]()
Значение
![]() получены для нормированной частоты
получены для нормированной частоты ![]() , поэтому ёмкость и индуктивность для
ненормированной частоты
, поэтому ёмкость и индуктивность для
ненормированной частоты ![]() определим из
условия
определим из
условия
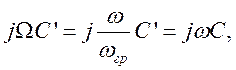
откуда
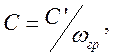 аналогично
аналогично 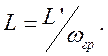
Например,
если принять ![]() то
то ![]() тогда
тогда
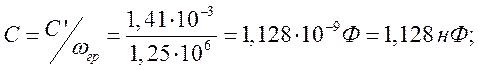
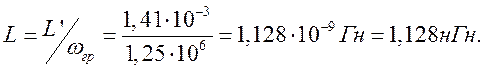
Схема фильтра нижних частот второго порядка для
принятых в примере значений ![]() и
и ![]() приведена на рис. 9.27.
приведена на рис. 9.27.
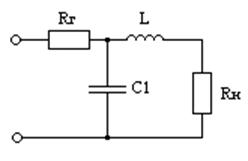
Рис. 9. 27. Схема ФНЧ второго порядка.
9. 11. Расчет фильтра Чебышева
1. Исходя из условий работы фильтра задают:
порядок фильтра ![]() ;
;
полосу пропускания ![]() ;
;
рабочее ослабление в полосе пропускания ![]() ;
;
граничную частоту полосы непропускания (задержание) ![]() .
.
2. Используя исходные данные определяют:
относительную частоту границы задержания
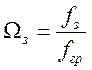 ;
;
коэффициент неравномерного ослабления в полосе пропускания
![]() ;
(9. 10)
;
(9. 10)
рабочее ослабление на частоте границы задержания
![]() (9. 11)
(9. 11)
квадрат АЧХ и затухания
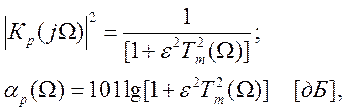 (9.
12)
(9.
12)
где ![]() , т. е. в полосе
пропускания;
, т. е. в полосе
пропускания; ![]() в полосе непропускания.
в полосе непропускания.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.