Министерство науки и образования Республики Казахстан
Северо-Казахстанский государственный университет им. М.Козыбаева
Факультет энергетики и машиностроения
Кафедра энергетики и приборостроения
Расчетно-графическая работа №1
Расчет линейных электрических цепей постоянного тока
по дисциплине «Основы электротехники»
Вариант № 3
Выполнил студент гр. зМС-07-у
Гусев А.Д.
Проверил ст. преподаватель
Зыкова Н.В.
______________________________
Петропавловск
2008
Задание
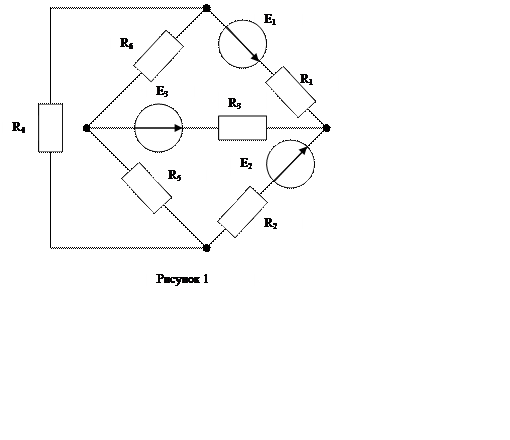
Для электрической цепи, приведенной на рисунке 1:
1) составить уравнения Кирхгофа;
2) рассчитать токи в цепи методом контурных токов;
3) рассчитать токи в цепи методом узловых напряжений;
4) составить баланс мощности;
5) построить потенциальную диаграмму.
|
№ варианта |
№ рисунка |
Е1, В |
Е2, В |
Е3, В |
R1, Ом |
R2, Ом |
R3, Ом |
R4, Ом |
R5, Ом |
R6, Ом |
|
3 |
1.9 |
14 |
25 |
28 |
5 |
2 |
8 |
2 |
2 |
6 |
Решение
1) Система уравнений по законам Кирхгофа
Цепь содержит
6 ветвей и 4 узла. По первому закону Кирхгофа количество уравнений составляет ![]() , а по второму
, а по второму ![]() , где
, где![]() - количество ветвей,
- количество ветвей, ![]() - количество узлов,
- количество узлов, ![]() - количество ветвей с источниками
тока.
- количество ветвей с источниками
тока.
Уравнения, составленные по первому закону Кирхгофа, для схемы на рисунке 1:
Для узла «1» I3+I6-I5=0;
Для узла «2» I1-I4-I6=0;
Для узла «3» -I1-I2-I3=0.
Уравнения, составленные по второму закону Кирхгофа, для схемы имеют вид:
для контура «4214» I4R4-I6R6-I5R5=0;
для контура «1231» I6R6+I1R1-I3R3=Е1-Е3;
для контура «1341» I3R3-I2R2+I5R5= E3-E2.
В соответствии с заданной схемой и исходными данными система уравнений по законам Кирхгофа будет иметь вид:
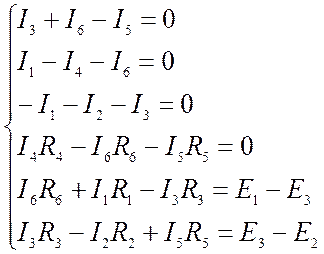
![]()
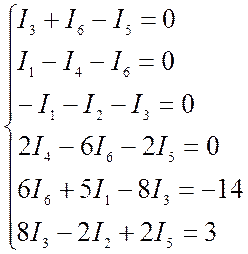
2) Метод контурных токов
При расчете
методом контурных токов число необходимых уравнений определяется только
выражением ![]() .
.
С учетом выбранного направления контурных токов составляется система из трех уравнений:
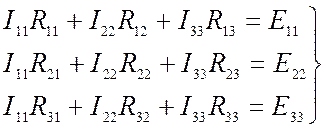
где R11, R22, R33 – собственные сопротивления соответственно 1, 2 и 3 контура (сумма сопротивлений всех ветвей, входящих в данный контур);
R12=R21 – общее сопротивление контуров 1 и 2 (если направление контурных токов в общей ветви для контуров 1 и 2 совпадают, то R12 положительно, в противном случае R12 отрицательно); R13=R31 – общее сопротивление контуров 1 и 3; R23=R32 – общее сопротивление контуров 2 и 3;
Enn - алгебраическая сумма ЭДС, включенных в ветви, образующие n-й контур.
R11=R4+R5+R6=2+2+6=10 Ом;
R22=R1+R3+R6=5+8+6=19 Ом;
R33=R2+R3+R5=2+8+2=12 Ом;
R12= R21= -R6= -6 Ом;
R13= R31=-R5=-2 Ом;
R23= R32=-R3=-8 Ом;
E11=0 В;
E22=Е1-Е3=14-28=-14 В;
E33=Е3-Е2= 28-25= -3 В.
С учетом найденных значений система получает вид:
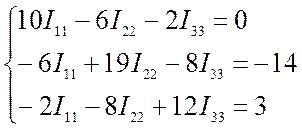
Решив составленную систему уравнений, например, методом Крамера, находим значения контурных токов I11 , I22 и I33.
![]()
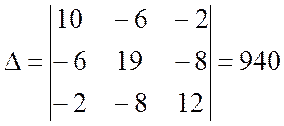
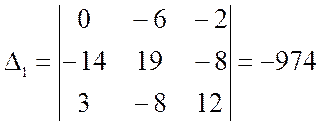
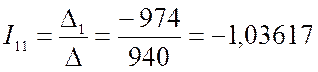
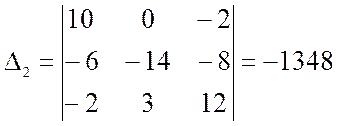
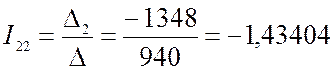
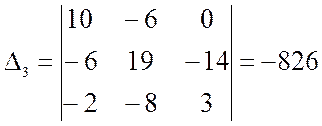
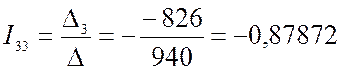
Через контурные токи определяются токи в ветвях:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
3) Метод узловых потенциалов.
Принимаем потенциал узла 4равным нулю, т.е. φ4=0
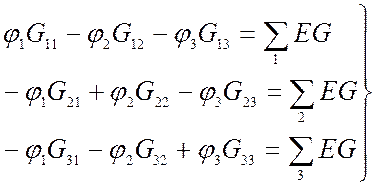

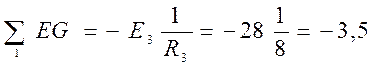
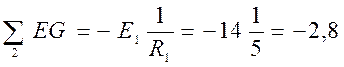
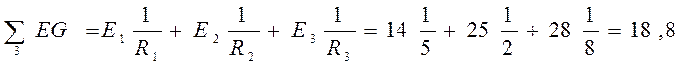
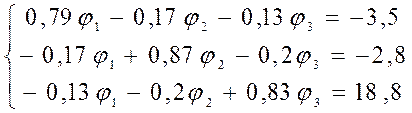
![]()
![]()

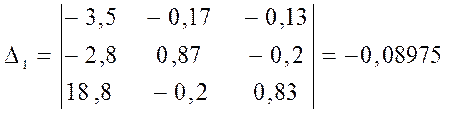
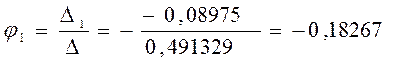
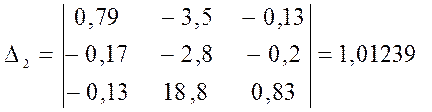
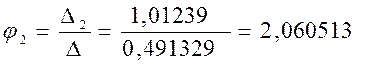

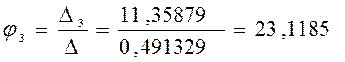
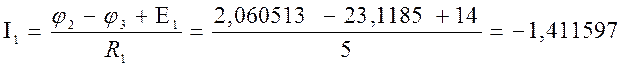
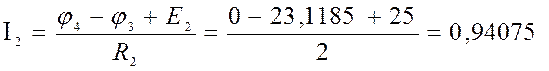
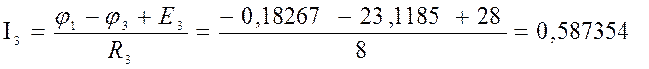
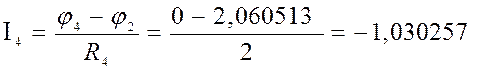
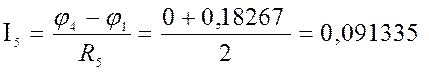
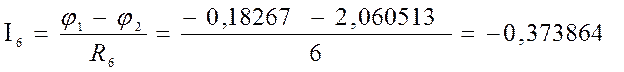
4) Баланс мощности
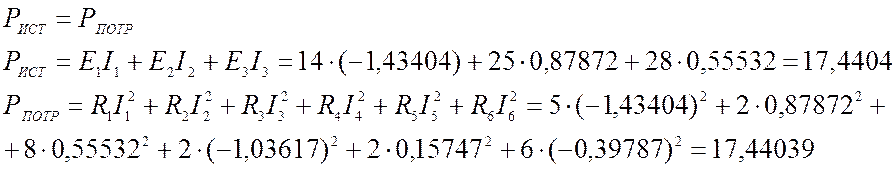
Ответ: I1=1,43 A; I2=0,88 А; I3=0,56 A; I4=-1,03 A; I5=0,15 A; I6=-0,39 A.

5) Потенциальная диаграмма
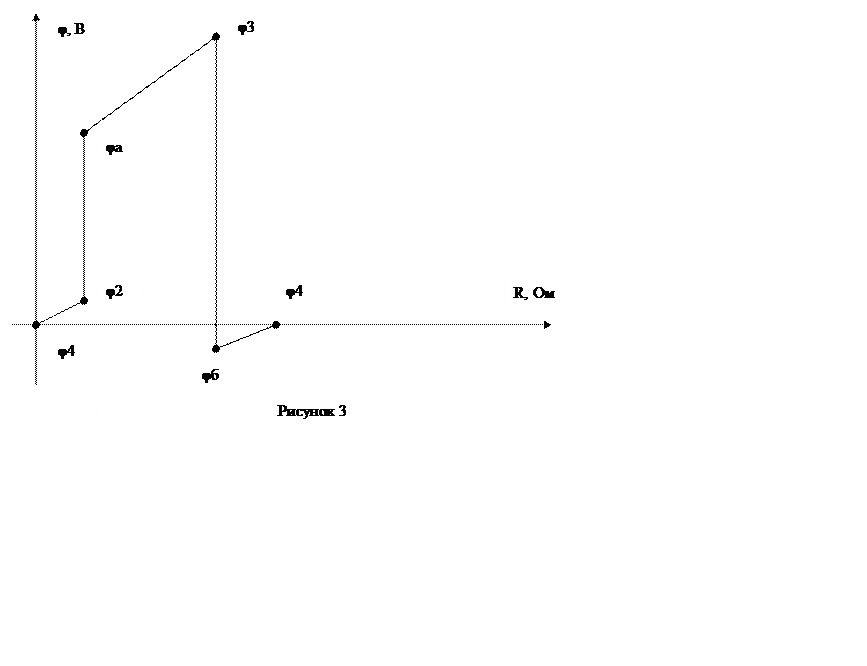
Для построения потенциальной диаграммы рассмотрим контур 42а3б4 электрической схемы, приведенный на рисунке 2.
Примем потенциал узла 4 равным нулю. Тогда в соответствии с направлением обхода контура и на основании рассчитанных выше значений токов, действующих в цепи, получим следующую векторную диаграмму (рисунок 3).
φ4 = 0;
φ2 = φ4 –I4R4 = 0 – (-1,04)·2 = 2,08 В;
φа = φб + Е1 = 2,08+14 = 16,08 В;
φ3 = φа – I1R1 = 16,08-(-1,43)·5 =16,08+7,15=23,23 В;
φб = φа – Е2 = 23,23-25 = -1,77 В;
φ4 = φб + I2R2 = -1,77+0,56·2 =-0,65≈0 В.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.