Расчет и построение частотных характеристик исходной системы и оценка устойчивости

В соответствии с заданной структурной схемой исходной системы:

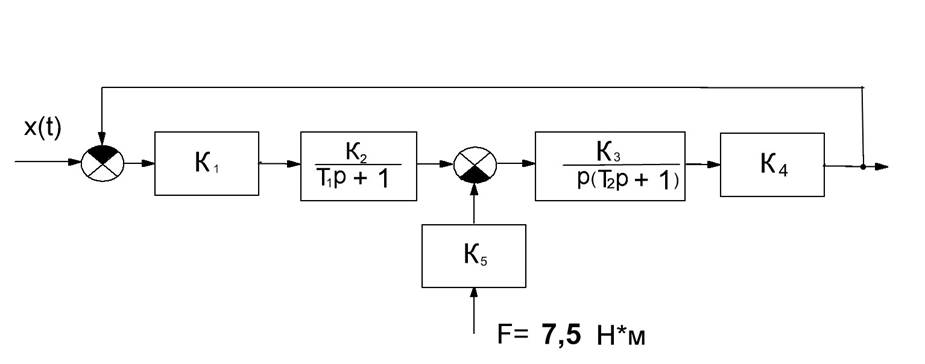
Где 

Запишем передаточную функцию исходной системы в разомкнутом состоянии:

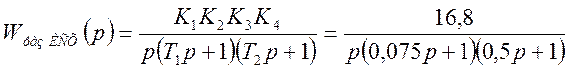
Оценку устойчивости исходной системы выполним по ее ЛАЧХ и ФЧХ. Для этого выполним их построение.

Отложим на оси частот частоты сопряжения ,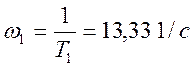

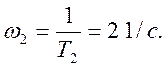
Исходная система является астатической, поэтому наклон первой асимптоты составляет -20 дБ/дек, которая пересекает ось 20lgK в точке .

После этого наклоны ЛАЧХ  после каждой частоты излома увеличиваются на -20 дБ/дек и ее наклон в области высоких частот составляет -60 дБ/дек.

Запишем по полученной передаточной функции исходной системы выражение для построения ФЧХ:

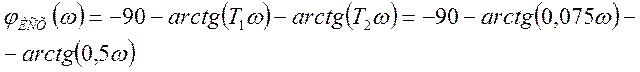
Задаваясь значениями частоты и подставляя в полученное выражение, выполним построение ФЧХ.

	0,01	0,1	1	2	5	5,6	13,33	100
	-90,33	-93,26	-120,86	-143,53	-178,76	-184,16	-216,47	-248.69

Т.к. ЛАЧХ пересекает ось частот позе, чем ФЧХ линию  -180 град, следовательно, исходная система является неустойчивой.

По ЛАЧХ определим частоту среза исходной системы. Она составляет 5,6 c^-1.

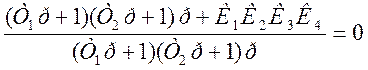
Определим критический коэффициент усиления исходной системы аналитически. Для этого запишем характеристическое уравнение:

- характеристическое уравнение.

Раскрываем скобки и приводим подобные:

         

Откуда

Для определения критического коэффициента усиления используем критерий Гурвица. Для этого составляем определитель из  коэффициентов характеристического уравнения и приравниваем его к нулю. В данном случае используем условие Гурвица для системы 3-го порядка.

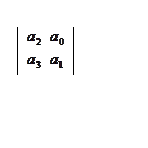Составляем определитель:

                                                              

где - искомый критический коэффициент усиления.

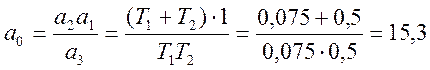
При таком коэффициенте система находится на границе устойчивости.