Разложение функции в ряд Фурье и определение коэффициентов ряда на различных промежутках

САРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ

КАФЕДРА «УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ»

ПРАКТИЧЕСКАЯ РАБОТА №2

по дисциплине «МОТС»

РАЗЛОЖЕНИЕ ФУНКЦИИ В РЯД ФУРЬЕ

Вариант №16

Выполнил: ст.гр. УИТ-32

Чупахина Н.Е.

Принял:

Ефремова Т.А.

2011

Цель работы: приобрести навыки разложения функции в ряд Фурье и определения коэффициентов ряда на различных промежутках.

Задание.

Дана функция .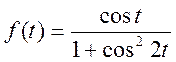

1) Исследовать функцию на четность.

2) Вычислить первые пять пар коэффициентов разложения в ряд Фурье функции f(t) на отрезке [0;2π].

3) Построить графики пяти гармоник в одной системе координат.

4) Выполнить гармонический синтез функции f(t) по гармоникам. Результаты синтеза отобразить графически.

Решение.

1)

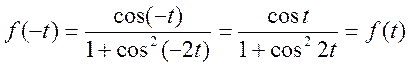
Условие четности выполняется, следовательно, функция является четной.

2) Разложение в ряд Фурье четной функции имеет вид:

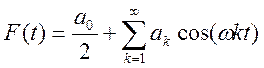
Коэффициенты ряда находятся по формуле:

,  ,

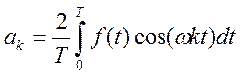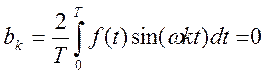где , .

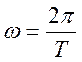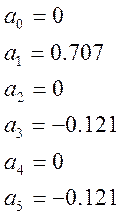
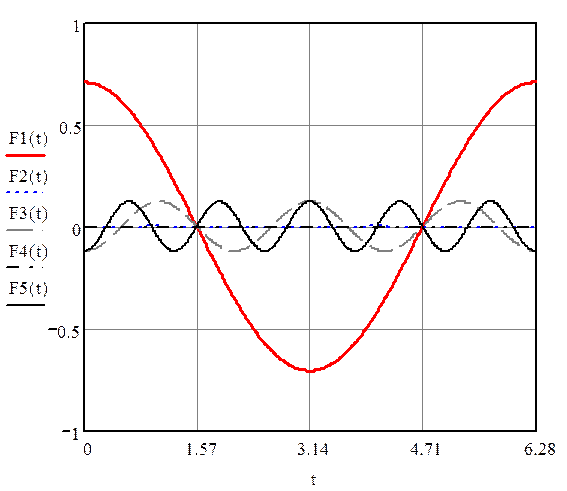
3) Построим графики гармоник

Рис. 1. Гармоники функции f(t)

4) Выполним гармонический синтез функции f(t) по гармоникам.

 

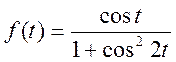
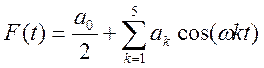
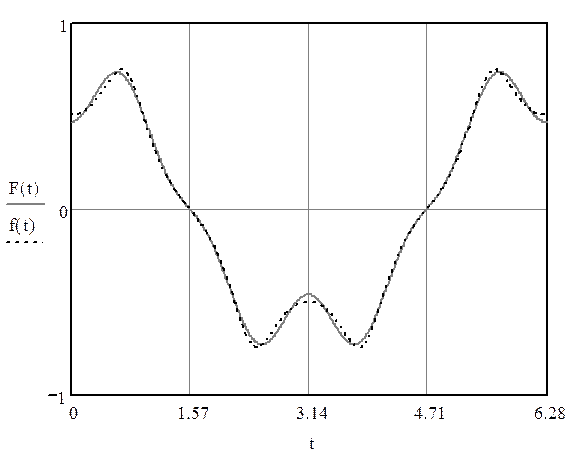
          Рис.2. Синтез функции f(x) по гармоникам

          Вывод: в ходе выполнения данной практической работы нами были приобретены навыки по разложению функции в ряд Фурье и определению коэффициентов ряда на различных промежутках. Мы провели гармонический анализ и синтез периодической функции и выяснили, что функция гармонического синтеза F(t) близка к исходной функции f(t) на отрезке [0;2π].