Прямое ![]() -преобразование
-преобразование
Докажем справедливость формулы
прямого ![]() -преобразования.
-преобразования.
Используя определение ![]() -преобразования, а также фильтрующее
свойство дельта-функции получим:
-преобразования, а также фильтрующее
свойство дельта-функции получим:
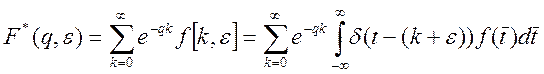
Запишем ![]() по
формуле обращения:
по
формуле обращения:
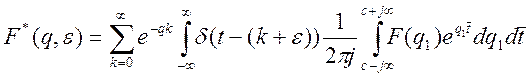
Внутренний интеграл по ![]() сходится равномерно относительно
сходится равномерно относительно ![]() . Поэтому порядок интегрирования
можно изменить, в результате чего получаем:
. Поэтому порядок интегрирования
можно изменить, в результате чего получаем:
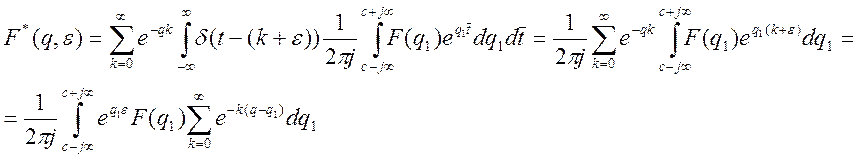
Переход от суммы интегралов к
интегралу от суммы будет заполнен, если ряд 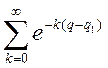 сходится
равномерно при
сходится
равномерно при ![]() . Чтобы удовлетворить это
условие, надо положить
. Чтобы удовлетворить это
условие, надо положить ![]() . Предполагая, что это
условие выполнено, можно записать:
. Предполагая, что это
условие выполнено, можно записать:
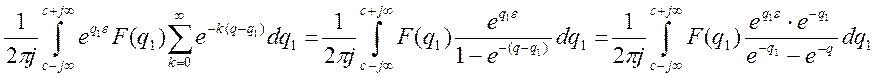
Разобьем прямую, по которой
производится интегрирование на отрезке длиной ![]() .
Тогда полученный интеграл будет иметь вид:
.
Тогда полученный интеграл будет иметь вид:
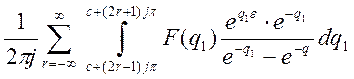
Произведем замену ![]() .
.
Тогда каждый из отрезков прямой
на плоскости ![]() , по которой идет интегрирование под
знаком суммы, отобразится в окружности на плоскости
, по которой идет интегрирование под
знаком суммы, отобразится в окружности на плоскости ![]() .
Отрезок на плоскости
.
Отрезок на плоскости ![]() , где
, где ![]() изменяется в пределах
изменяется в пределах ![]() .
.
Обозначая эти окружности как ![]() , можно получить следующее
соотношение:
, можно получить следующее
соотношение:
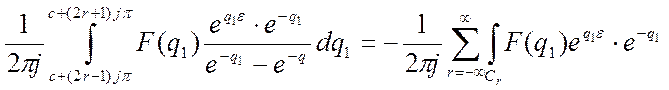
В последнем равенстве введем обозначение:
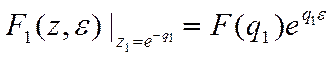
При чем окружность ![]() при изменении частоты
при изменении частоты ![]() в пределах
в пределах ![]() обходится
в отрицательном направлении. Изменяя направление интегрирования, получаем:
обходится
в отрицательном направлении. Изменяя направление интегрирования, получаем:
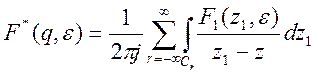 (1)
(1)
Здесь окружность ![]() , которая задается формулой
, которая задается формулой ![]() обходится в положительном направлении
при изменении частоты
обходится в положительном направлении
при изменении частоты ![]() в пределах
в пределах ![]() .
.
Заметим, что замена комплексной
переменной по формуле ![]() отображает правую
полуполосу плоскости переменной
отображает правую
полуполосу плоскости переменной ![]() . Эта полуполоса
определена соотношениями:
. Эта полуполоса
определена соотношениями:
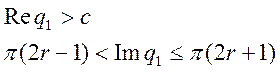
внутри окружности ![]() . Поскольку функция
. Поскольку функция ![]() является аналитической в правой полуплоскости
и на прямой, по которой производится интегрирование, то есть в области, где
является аналитической в правой полуплоскости
и на прямой, по которой производится интегрирование, то есть в области, где ![]() , то функция
, то функция ![]() является
аналитической внутри каждой окружности, по которой вычисляется интеграл в
выражении (1) и на самой окружности. Подынтегральное выражение в уравнении (1)
является аналитической функцией внутри окружности
является
аналитической внутри каждой окружности, по которой вычисляется интеграл в
выражении (1) и на самой окружности. Подынтегральное выражение в уравнении (1)
является аналитической функцией внутри окружности ![]() ,
за исключением точки
,
за исключением точки ![]() , которая лежит внутри
, которая лежит внутри ![]() , где
, где ![]() .
Поэтому справедливо неравенство:
.
Поэтому справедливо неравенство:
![]()
По интегральной теореме Коши можно определить каждый из интегралов, стоящих вод знаком суммы в выражении (1).
При r=0 имеем:
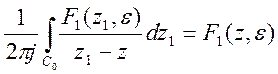
Здесь в соответствии с
обозначениями, ![]() - окружность, ее уравнение
-
- окружность, ее уравнение
- ![]() . При чем
. При чем ![]() меняется
в пределах
меняется
в пределах ![]() . Теперь найдем интеграл по
окружности
. Теперь найдем интеграл по
окружности ![]() , для которой уравнение окружности
имеет вид -
, для которой уравнение окружности
имеет вид - ![]() , где
, где ![]() .
Здесь следует отметить, что подынтегральное выражение является аналитической
функцией внутри окружности
.
Здесь следует отметить, что подынтегральное выражение является аналитической
функцией внутри окружности ![]() , за исключением
точки
, за исключением
точки ![]() .
.
Таким образом получаем:
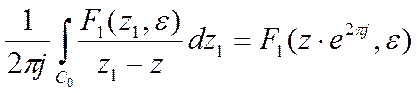
Аналогично для любой окружности ![]() , то есть для любого слагаемого в
уравнении (1) будем иметь:
, то есть для любого слагаемого в
уравнении (1) будем иметь:
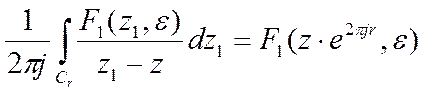
Используя это выражение и уравнение (1) получаем:
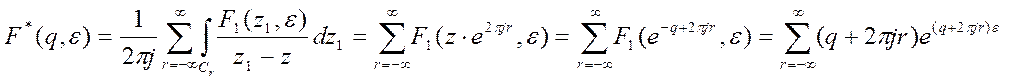 Таким
образом, справедливость формулы прямого
Таким
образом, справедливость формулы прямого ![]() -преобразования
доказана.
-преобразования
доказана.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.