Проектирование системы автоматического управления, структура и параметры которой удовлетворяли заданные требования к качеству регулирования, страница 3

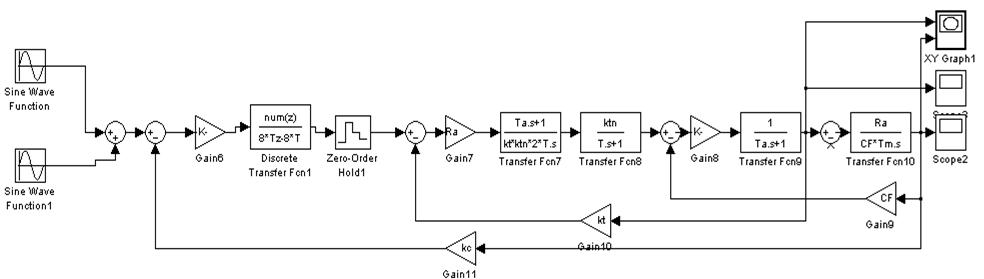
Рис. 38. Структурная схема для построения зависимостей, , без фильтра 

T = 0.05*Ta

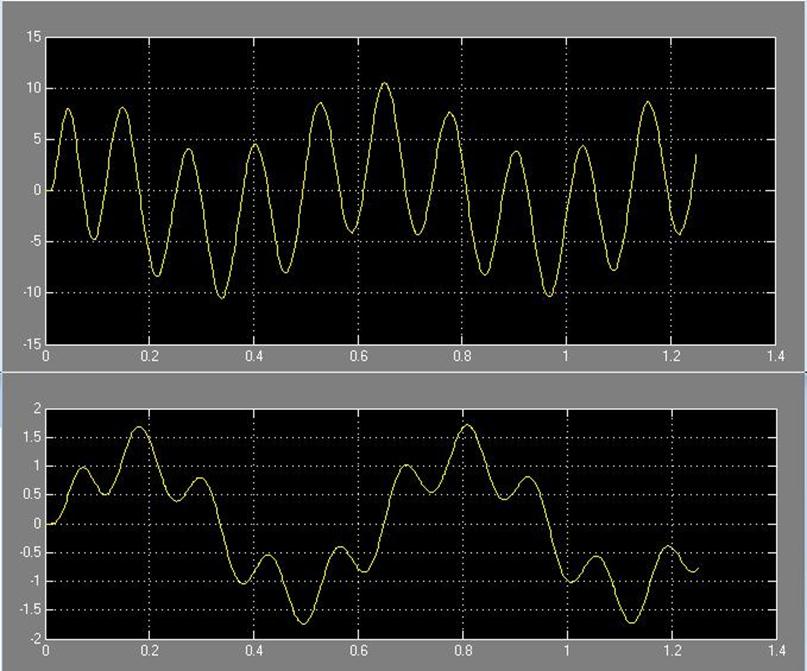
Рис. 39  Зависимость системы i(t) и w(t) с цифровым регулятором соответственно

T = 0.5*Ta

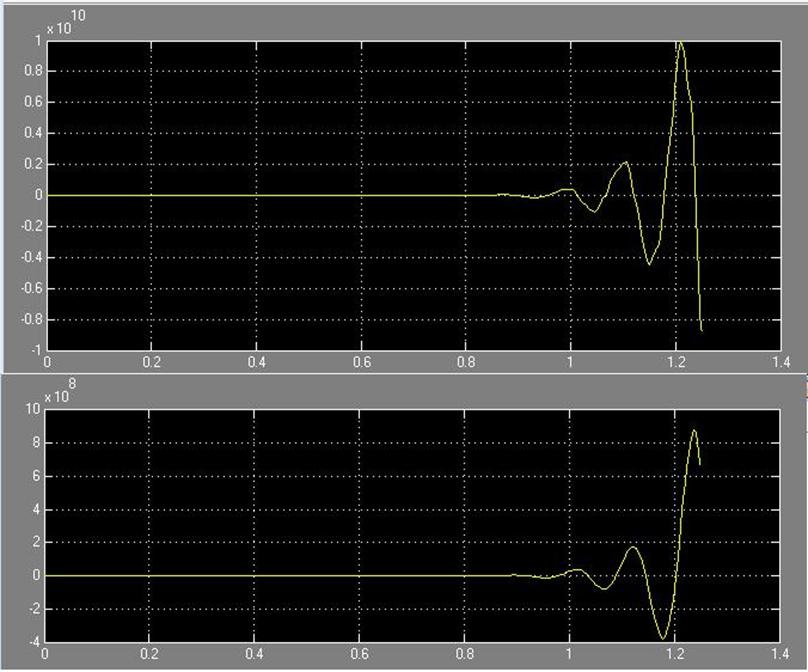
Рис. 40  Зависимость системы i(t) и w(t) с цифровым регулятором соответственно

     

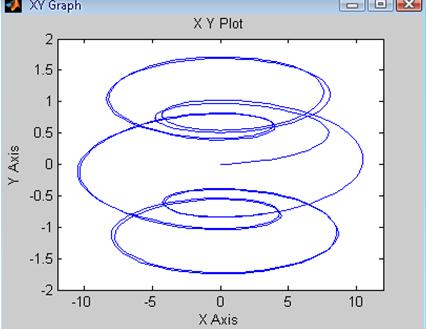
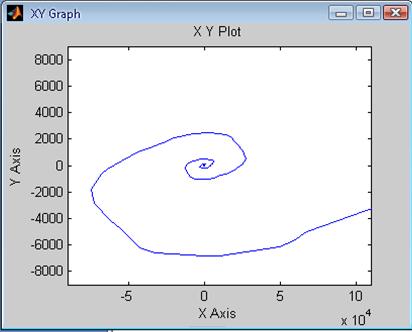
Рис. 41 Зависимость  системы с                    Рис.42 Зависимость системы с

цифровым регулятором скорости                          цифровым регулятором скорости

 при T = 0.05*Ta  с фильтром                                       при T = 0.5*Ta с фильтром

10.1.5. Построение зависимостей , ,  при подачи на вход помехи с фильтром

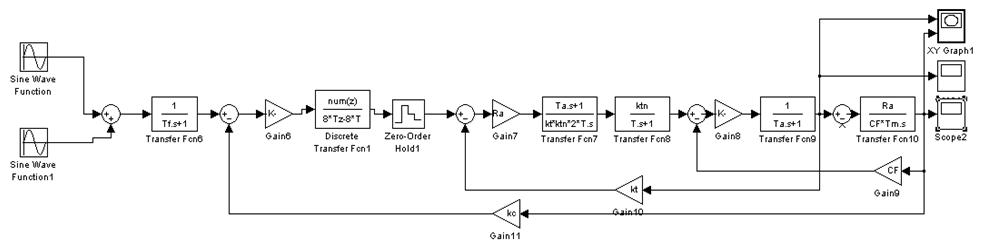
Рис. 43 Структурная схема для построения зависимостей, , с фильтром

T = 0.05*Ta

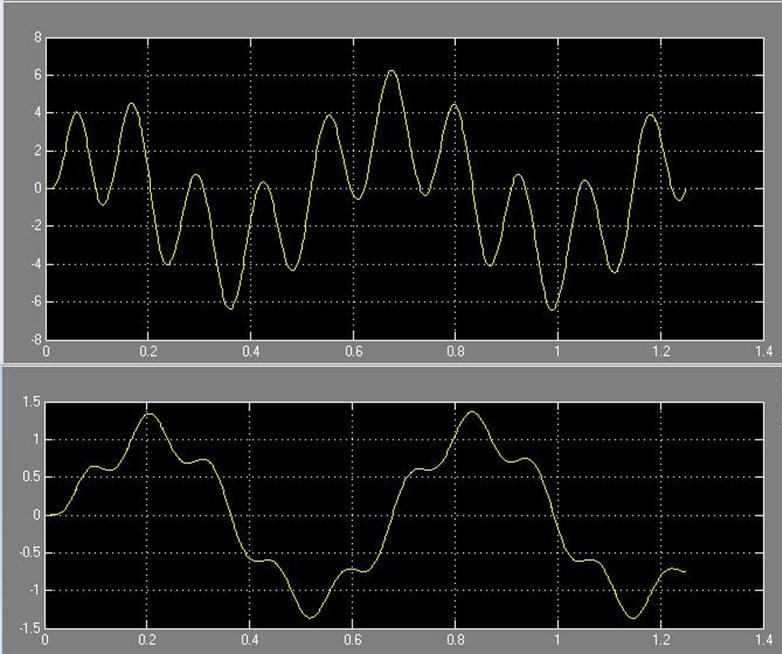
Рис. 44  Зависимость системы i(t) и w(t) с цифровым регулятором с фильтром

T = 0.5*Ta

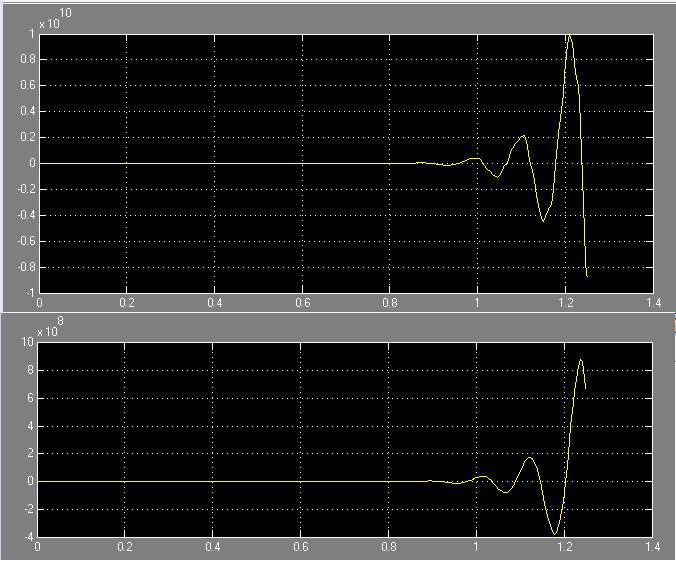
Рис. 45  Зависимость системы i(t) и w(t) с цифровым регулятором с фильтром

 

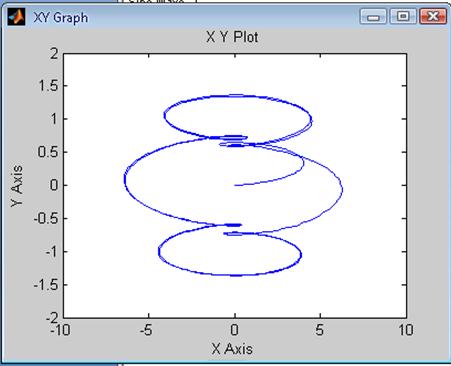
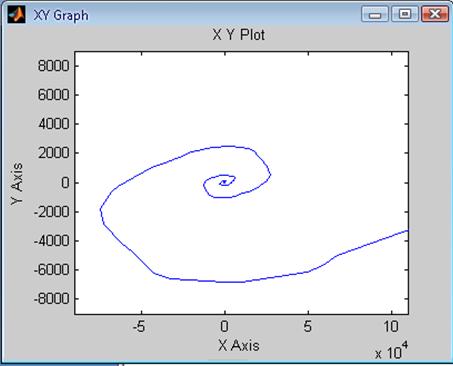
Рис. 46 Зависимость  системы с                    Рис.47 Зависимость системы с

цифровым регулятором скорости                          цифровым регулятором скорости

 при T = 0.05*Ta                                                       при T = 0.5*Ta

10.1.6. Определение коэффициента передачи

• Численным методом

- амплитуда основной гармоники:

- амплитуда сигнала на выходе системы:

       Т.о. коэффициент передачи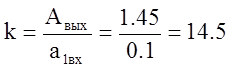           

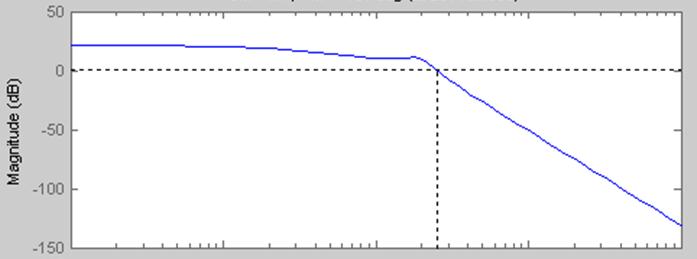
• По ЛАЧХ

Рис. 21 ЛАЧХ

По графику найдем L(w): , тогда коэффициент передачи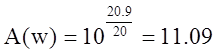  

10.2. Билинейные преобразования

10.2.1. Найдем запасы устойчивости по амплитуде и по фазе

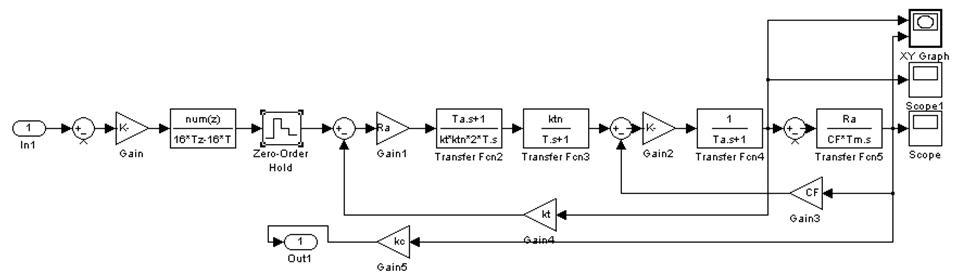
Рис. 50 Структурная схема для определения запасов

T = 0.05*Ta

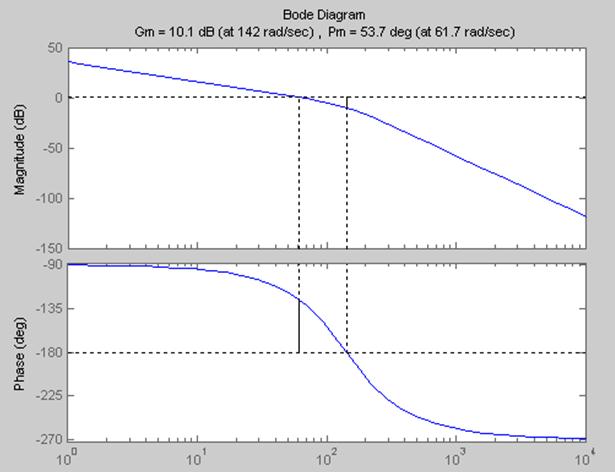
Рис. 51 Запасы: ,  

T = 0.5*Ta

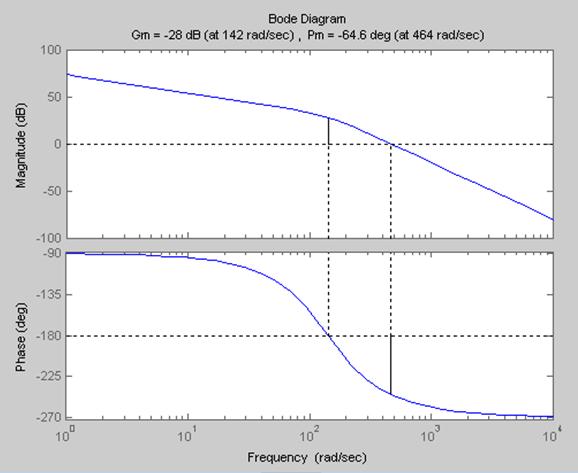
Рис. 25 Запасы:

 à система неустойчива

САУ не устойчива, как и при Z-преобразовании.

10.2.2. Построение зависимостей , ,  при подаче на вход единичного ступенчатого сигнала

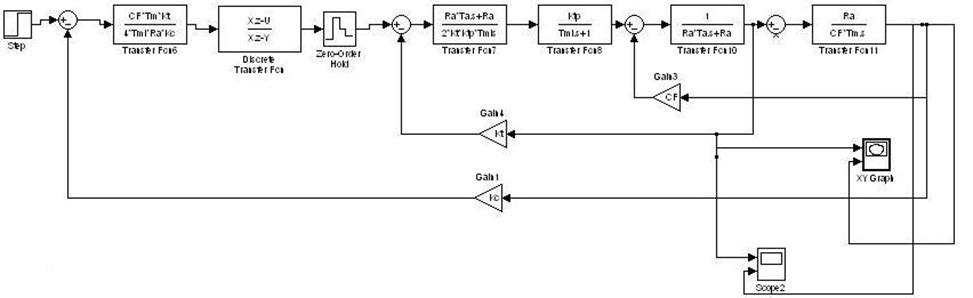
Рис. 53 Структурная схема

T = 0.05*Ta

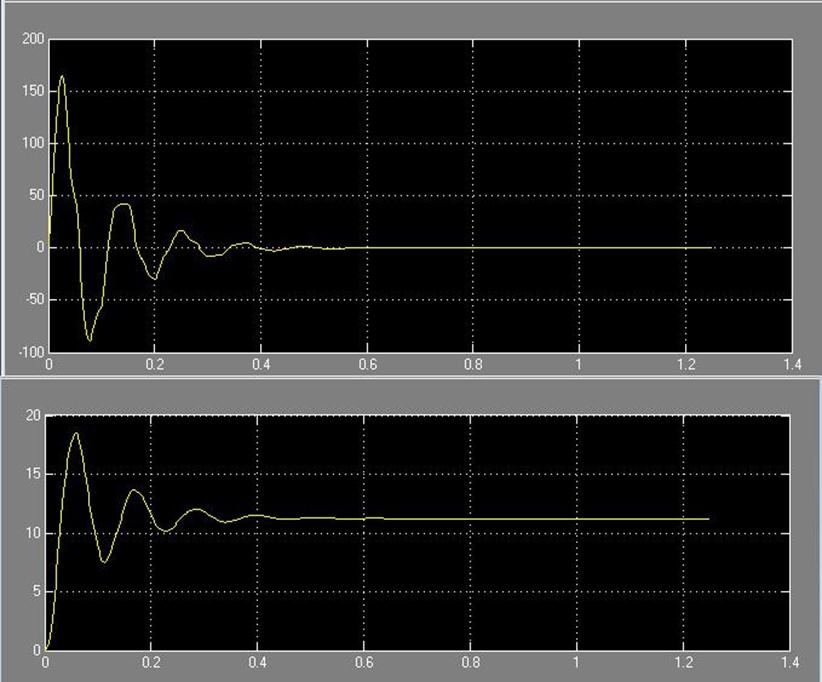
Рис. 54 Зависимость системы i(t) и w(t) с цифровым регулятором соответственно

Из графика можно определить получившиеся показатели качества:

- перерегулирование: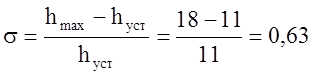  

- время регулирования:

T = 0.5*Ta

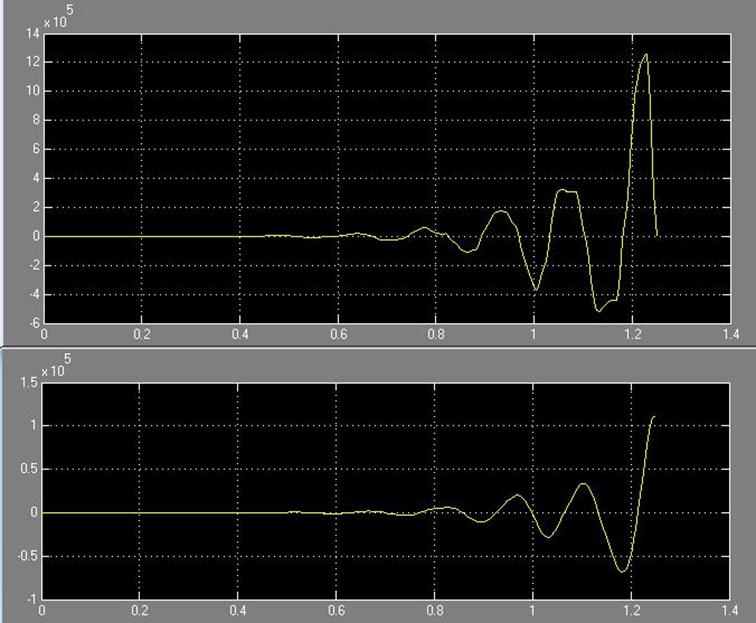
Рис. 55 Зависимость системы i(t) и w(t) с цифровым регулятором соответственно

   

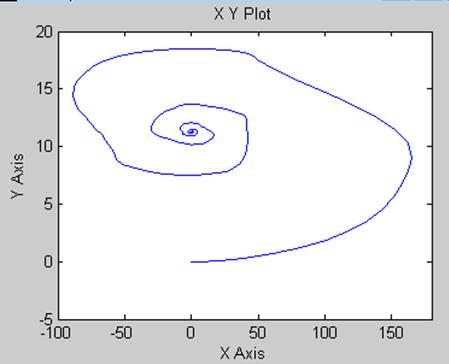
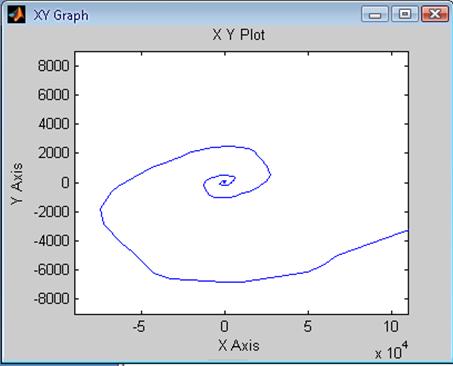
Рис. 56 Зависимость  системы с                    Рис.57 Зависимость системы с

цифровым регулятором скорости                          цифровым регулятором скорости

 при T = 0.05*Ta                                                       при T = 0.5*Ta

Подтверждаем данными билинейными преобразованиями, что при Т=0.5Та система также неустойчива, как и при Z-преобразованиях.

Перерегулирование больше требуемого, следовательно, нужно поставить фильтр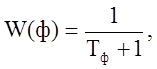   

T =0.05*Ta

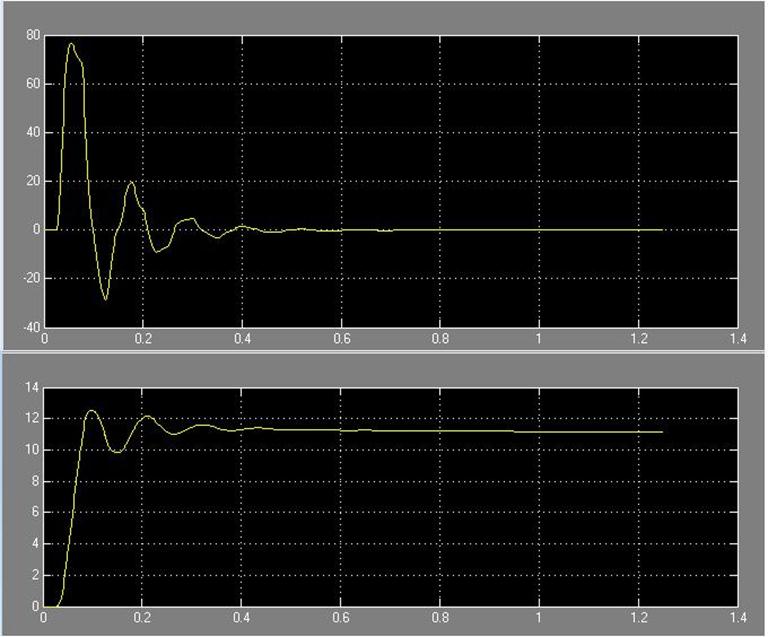
Рис. 58  Зависимость системы i(t) и w(t) с цифровым регулятором соответственно

- перерегулирование: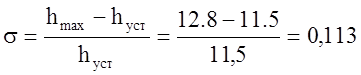  

- время регулирования: 

T =0.5*Ta

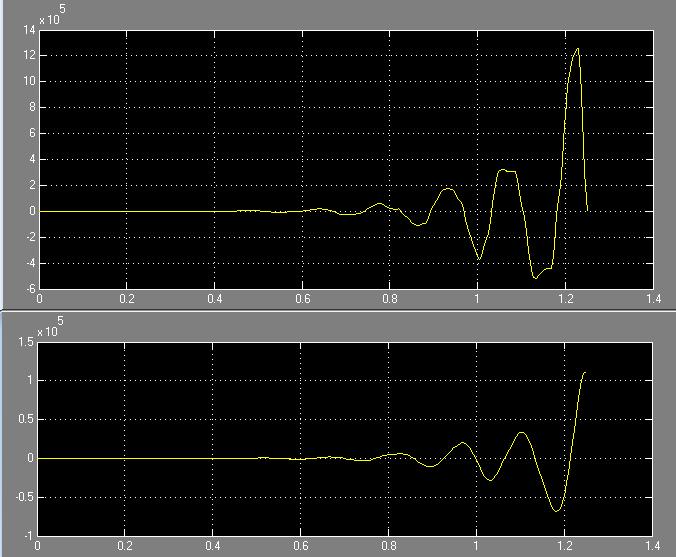
Рис. 59  Зависимость системы i(t) и w(t) с цифровым регулятором соответственно

 

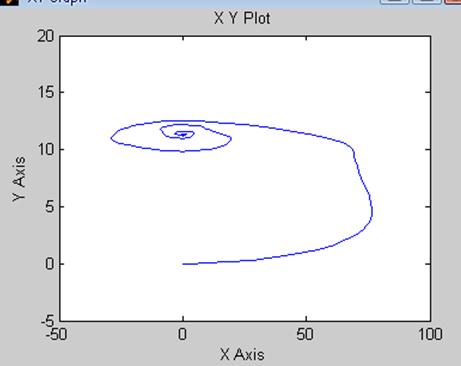
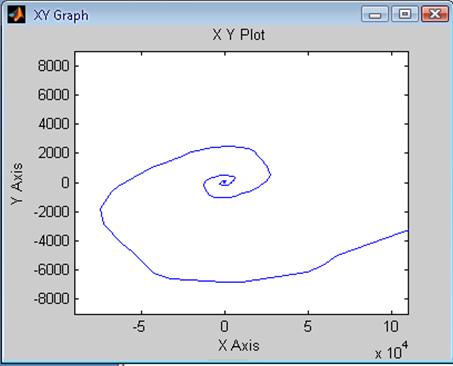
Рис. 60 Зависимость  системы с                    Рис.61 Зависимость системы с

цифровым регулятором скорости                          цифровым регулятором скорости

 при T = 0.05*Ta                                                       при T = 0.5*Ta

10.2.3. Построение зависимостей , ,  при ступенчатом приложении нагрузки

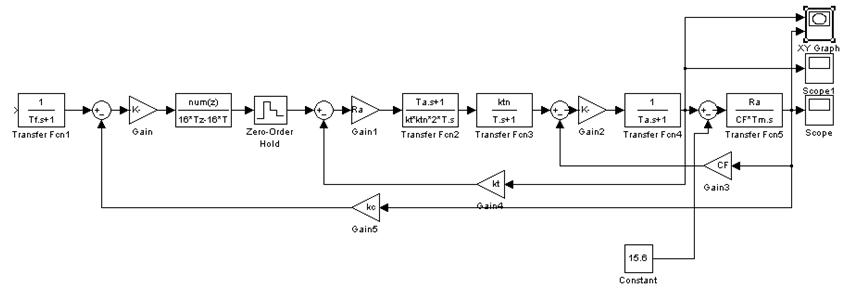
Рис. 62 Структурная схема для построения зависимостей , ,  

T = 0.05*Ta

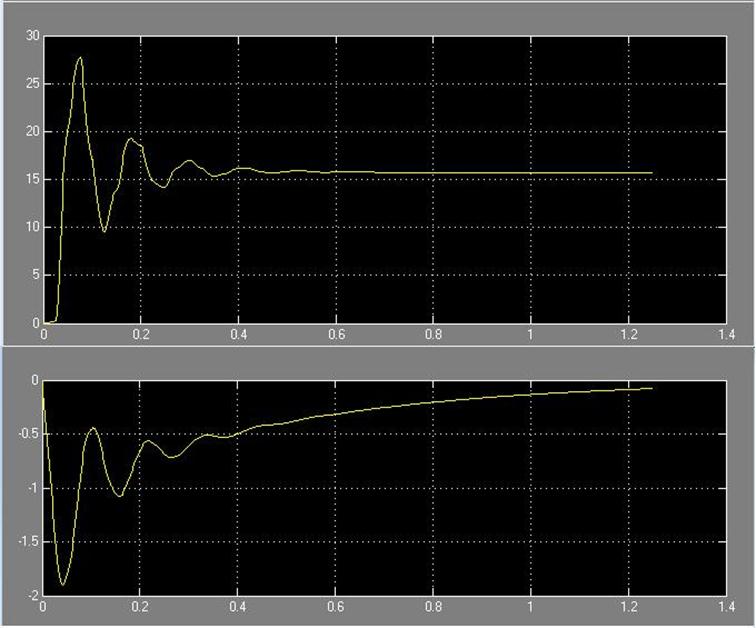
Рис. 63  Зависимость системы w(t) и i(t) соответственно

T = 0.5*Ta

Рис.64  Зависимость системы w(t) и i(t) соответственно

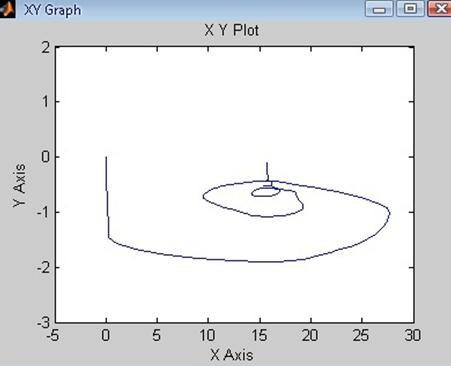
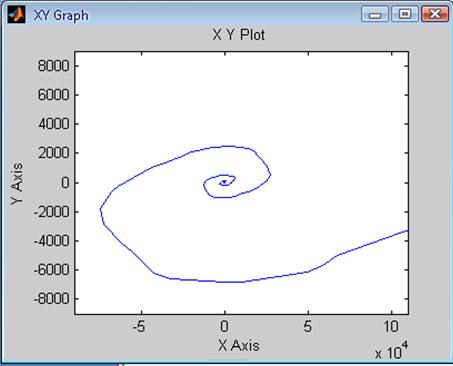
Рис. 65 Зависимость  системы с                    Рис.66 Зависимость системы с

цифровым регулятором скорости                          цифровым регулятором скорости

 при T = 0.05*Ta                                                       при T = 0.5*Ta

Определение установившейся ошибки

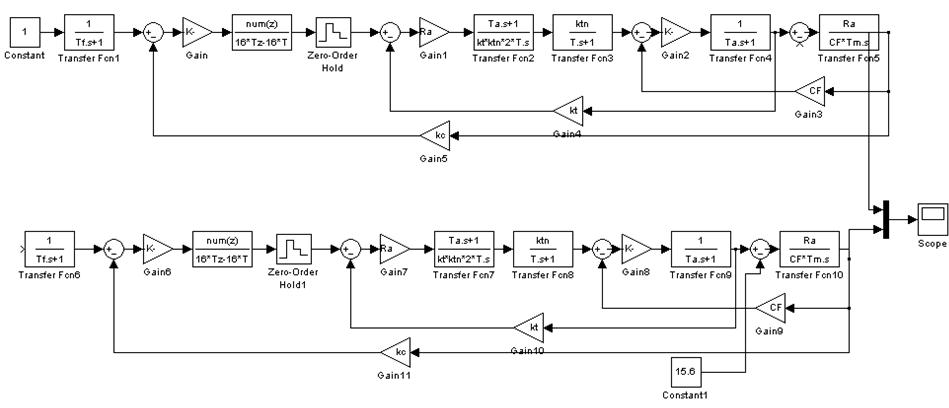
Рис. 66.1 Структурная схема

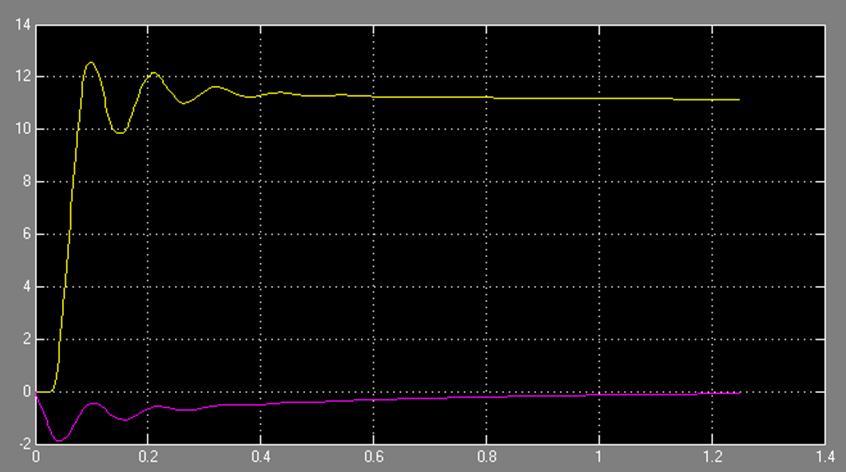
Рис. 66.2 Характеристика

10.2.4 Построение зависимостей , ,  при подачи на вход помехи без фильтра

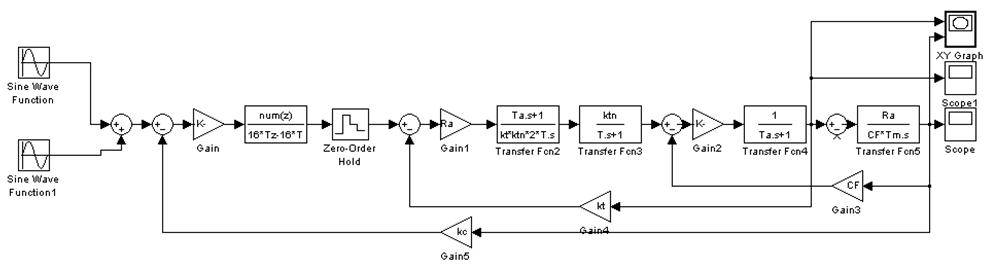
Рис. 67  Структурная схема для построения зависимостей , ,  без фильтра

T = 0.05*Ta

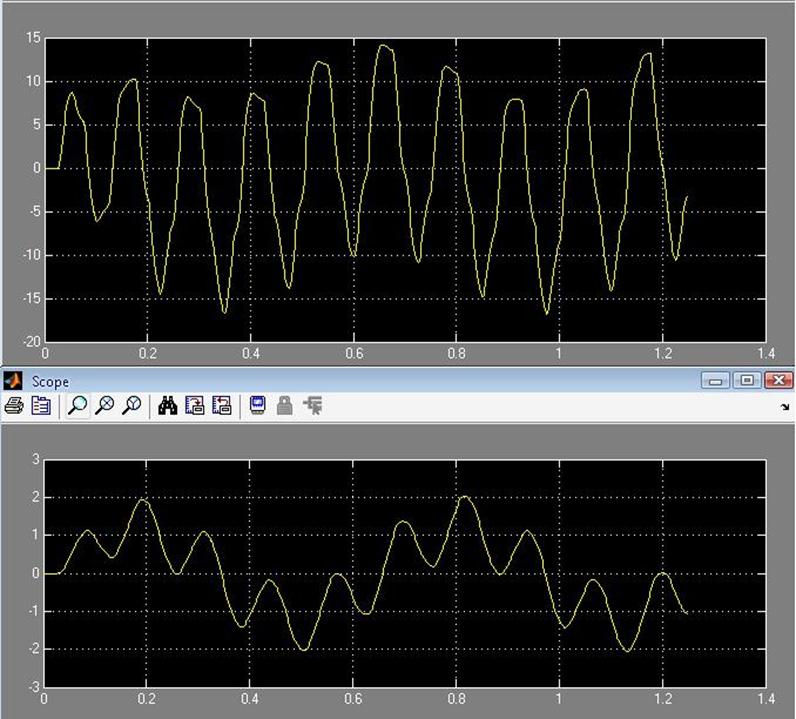
Рис. 68  Зависимость системы w(t) и i(t) соответственно

T = 0.5*Ta

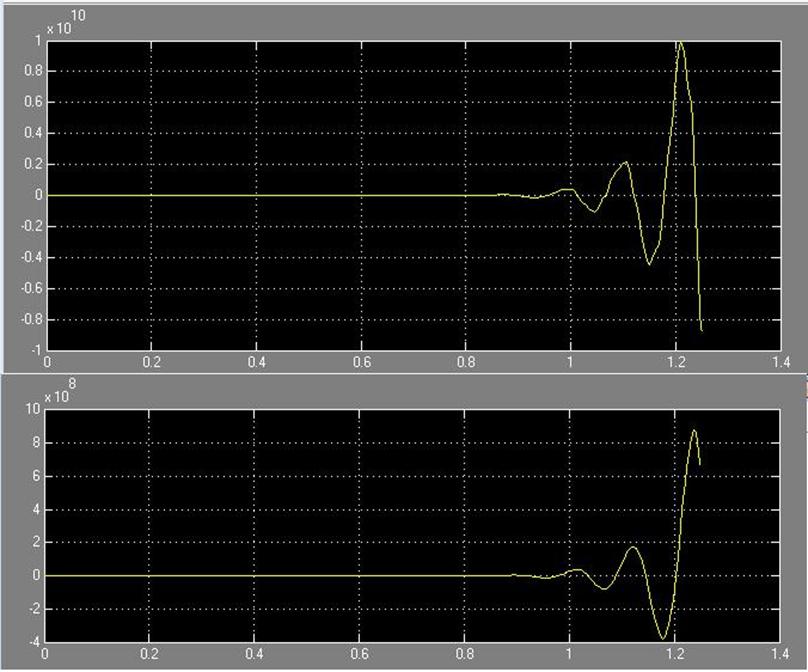
Рис. 69  Зависимость системы w(t) и i(t) соответственно

 

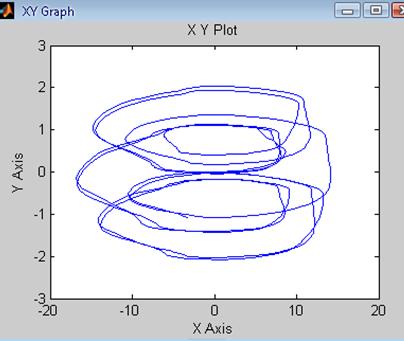
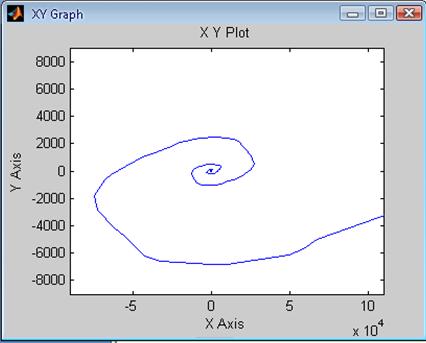
Рис.70 Зависимость  системы с                     Рис.71 Зависимость системы с

цифровым регулятором скорости                          цифровым регулятором скорости

 при T = 0.05*Ta                                                       при T = 0.5*Ta

10.2.4 Построение зависимостей , ,  при подачи на вход помехи с фильтром

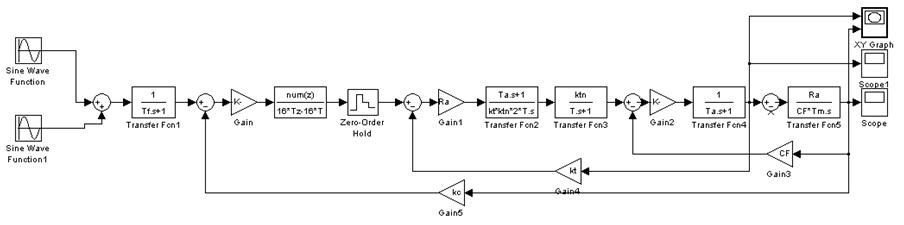
Рис. 72  Структурная схема для построения зависимостей , ,  с фильтром

T = 0.05*Ta

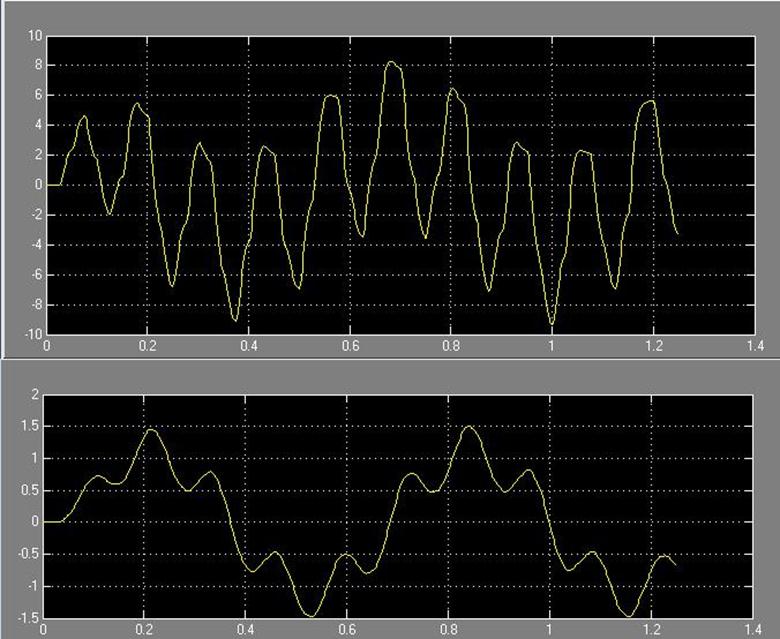
Рис. 73 Зависимость системы w(t) и i(t) соответственно

T = 0.5*Ta

Рис. 74 Зависимость системы w(t) и i(t) соответственно

    

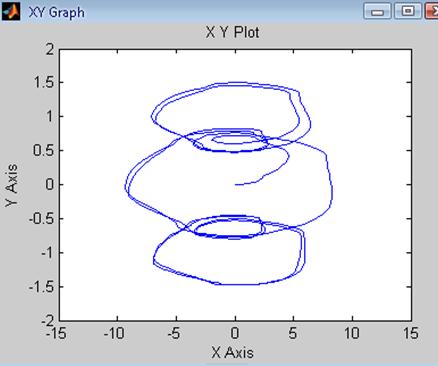
Рис.75 Зависимость  системы с                     Рис.76 Зависимость системы с

цифровым регулятором скорости                          цифровым регулятором скорости

 при T = 0.05*Ta                                                       при T = 0.5*Ta

10.2.6. Определение коэффициента передачи

• Численным методом

- амплитуда основной гармоники:

- амплитуда сигнала на выходе системы:

       Т.о. коэффициент передачи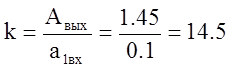           

• По ЛАЧХ

Рис. 21 ЛАЧХ

По графику найдем L(w): , тогда коэффициент передачи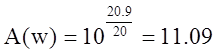  

Заключение

Составим сопоставительную таблицу показателей качества САУ

Показатели качества Тип регулятора  скорости			σ	tP, с	ΔL, дБ	Δφ, град	Коэффициент передачи на частоте ω = ω1
							Численный эксперимент	По ЛАЧХ
Система подчиненного регулирования			0,55	0,12	-9,59	33,8	14.5	11.09
Цифровой регулятор	Стандартное Z- преобразование	Т=0.05 Тm	0,081	0,08	-10,4	55	14.5	11.09
		Т=0.5Тm	система неустойчива
	Билинейное  Z- преобразование	Т=0.05 Тm	0,113	0,18	-10,1	53,7	14.5	11.09
		Т=0.5Тm	система неустойчива
Задание			0,08	0,1	20	π/6

На основании вышеприведенной таблицы можно сделать следующие выводы:

     -перерегулирование для всех вариантов синтеза примерно одинаково и удовлетворяет требованиям задания;

     -время регулирования удовлетворяет заданию во всех случаях.

   На основании четырех вариантов анализа системы с цифровым регулятором скорости можно сделать выводы:

     -переходные характеристики непрерывной и дискретной систем практически совпадают;

     -при усложнении способа дискретизации непрерывной системы (переход от стандартных Z - преобразований к билинейному преобразованию) дискретная система все больше приближается к непрерывной.

Библиографический список

1. Бесекерский В.А., Попов Е.П., «Теория систем автоматического регулирования», издательство «Наука», Главная редакция физико-математической литературы, М., 1975, 768 стр.

2. Расчет системы управления автоматизированным электроприводом. Методические указания к курсовому проектированию по дисциплине «Теория автоматического управлении» / В.Л. Тимофеев. Н. Тагил: НТИ(ф) ГОУ УГТК-УПИ. 2002. 17с.

3.Тимофеев В.Л., Баркова О.Н., Исаев И.Н. “Технические и экономические расчеты в курсовых и дипломных проектах” учебное пособие, Нижний Тагил, НТИ(ф) УГТУ-УПИ, 2006