Проектирование системы автоматического управления, структура и параметры которой удовлетворяли заданные требования к качеству регулирования, страница 2

Т.о. структурная схема имеет вид:

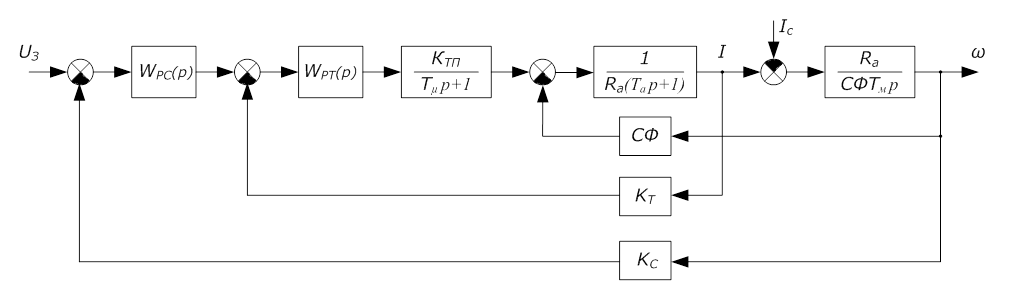
Рис. 5 Структурная схема САУ

7.1. Синтез регулятора тока

Синтез регулятора тока происходит без внутренней ОС по противоЭДС электродвигателя.

Передаточная функция разомкнутой системы имеет вид:

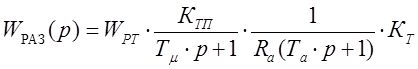
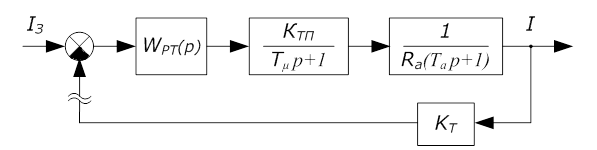
Рис. 6 Расчетная схема контура тока

Желаемая передаточная функция разомкнутого контура тока имеет вид:

.

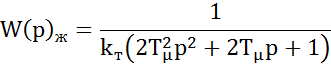
Приравнивая , выражаем передаточную функцию регулятора тока:

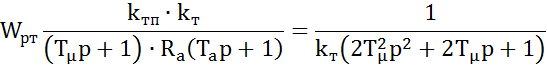
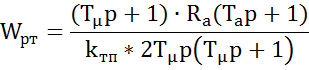
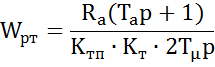
7.2.  Синтез контура скорости

Расчет регулятора скорости ведем без учета нагрузки. Нагрузку будем учитывать при анализе системы

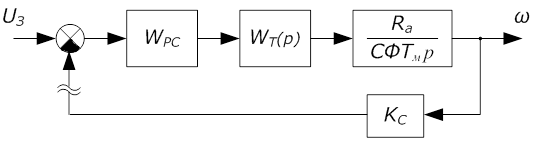
Рис. 7 Расчетная схема контура скорости

Желаемая разомкнутая функция регулятора скорости:

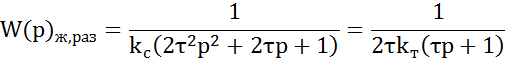
Реальная передаточная функция контура скорости:

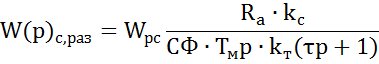
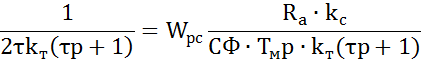
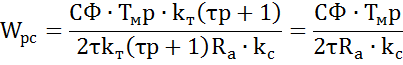
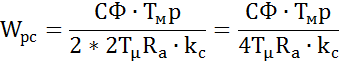
В результате мы получили П – регулятор скорости. По заданию требуется обеспечить астатизм второго порядка по отношению к сигналу задания. Т. о. в качестве регулятора скорости применяем ПИ – регулятор со следующей передаточной функцией:

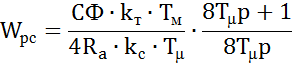
7.3 Компенсирующий сигнал

 – компенсирующий сигнал.

= 0,229

= 0,041

Так как влияние обратной связи противоЭДС не сильное, то компенсирующий сигнал не используется.

8. Анализ системы подчиненного регулирования

Анализ системы подчиненного регулирования будем производить с помощью программы MATLAB 7.9

8.1. Определение запасов устойчивости системы

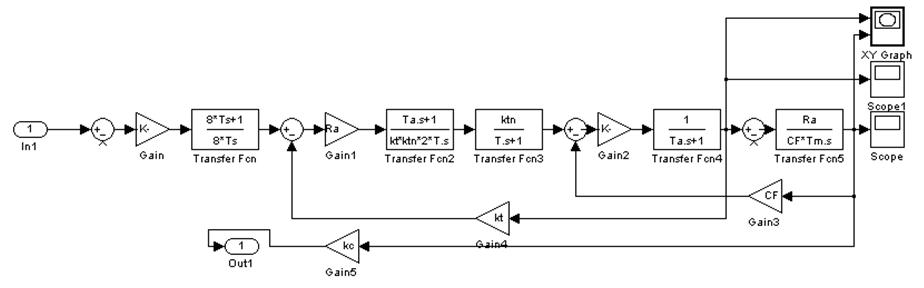
Рис. 8 Разомкнутая структурная схема САУ

Определяем запасы устойчивости по построенным частотным характеристикам (рис. 10).

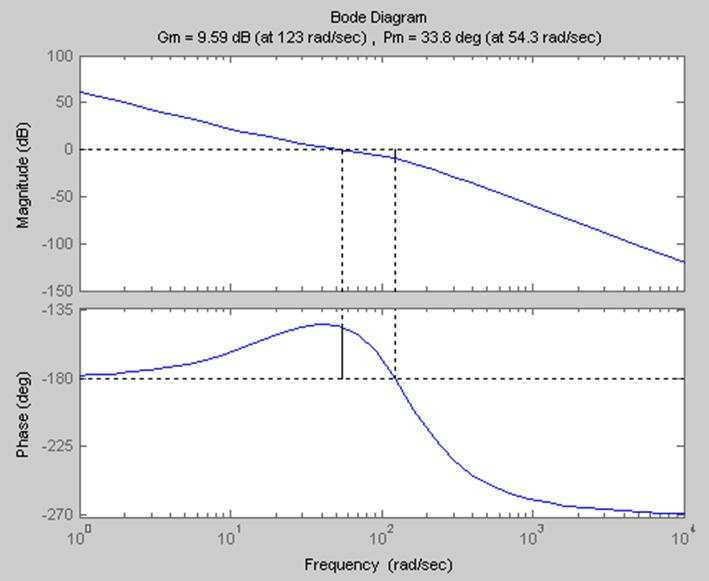
Рис. 9  Запасы: , 

 ,   à система устойчива.

8.2 Построение зависимостей , ,  при подаче на вход единичного ступенчатого сигнала

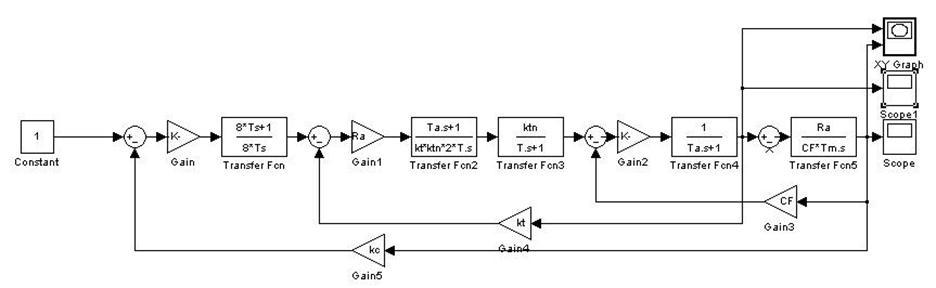
Рис. 10. Структурная схема для построения зависимостей , ,  

 

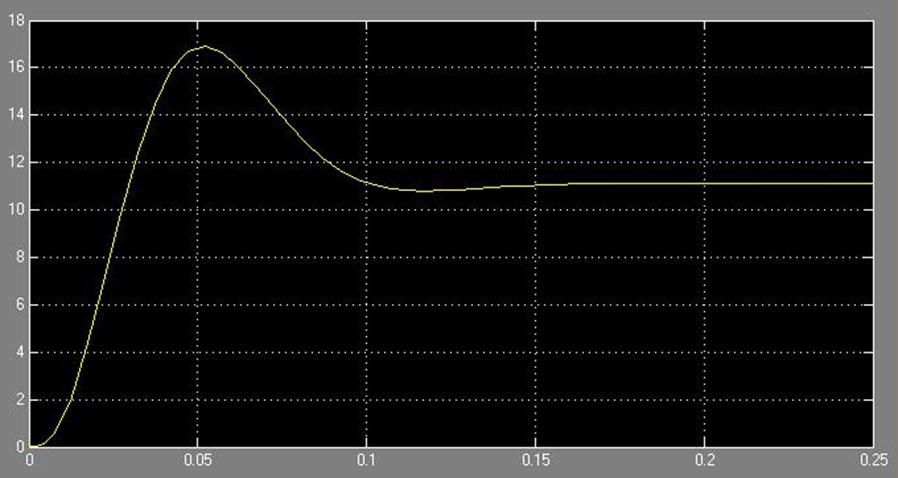
Рис 11. График переходной функции

Из графика можно определить получившиеся показатели качества:

- перерегулирование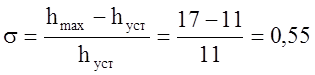

- время регулирования

Сравнивая с техническим заданием, видим, что перерегулирование не удовлетворяет заданному, следовательно, необходимо поставить фильтр:

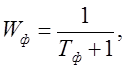 где

Тогда график переходной функции будет иметь вид:

 

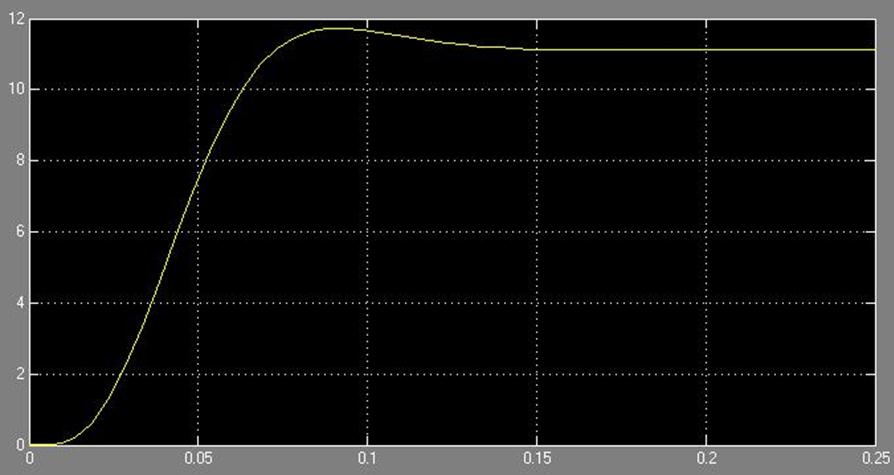
Рис 12. График переходной функции с фильтром

Откуда видно, что

- перерегулирование .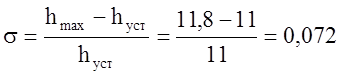

- время регулирования

Время регулирования получается больше, чем в задании, это может быть следствием слишком жестких требований, предъявляемых к приводу, поэтому время регулирования оставляем без изменений.

Построим зависимости  и w(t)

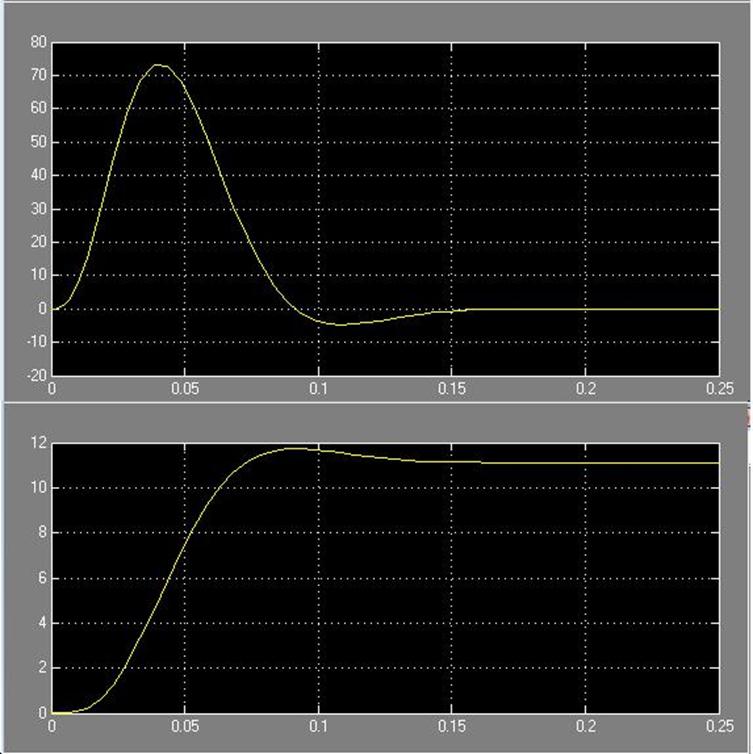
Рис. 13. Зависимости  и   w(t ) соответственно

Построим зависимость

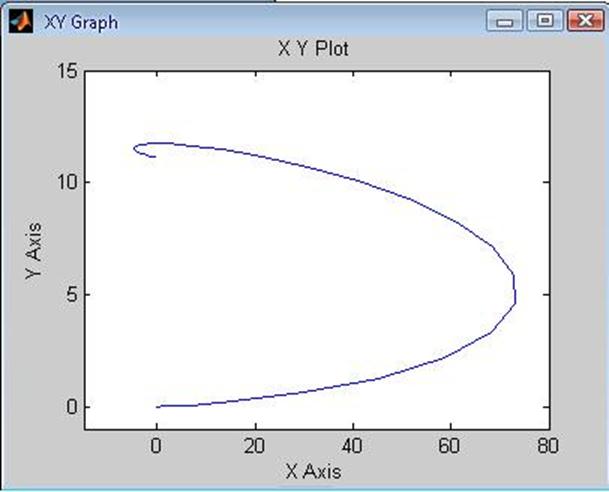
Рис 14. Динамическая электромеханическая характеристика

8.3 Построение графиков реакции САУ на ступенчатое приложение нагрузки Ic/Iн и соответствующей электромеханической характеристики

, 

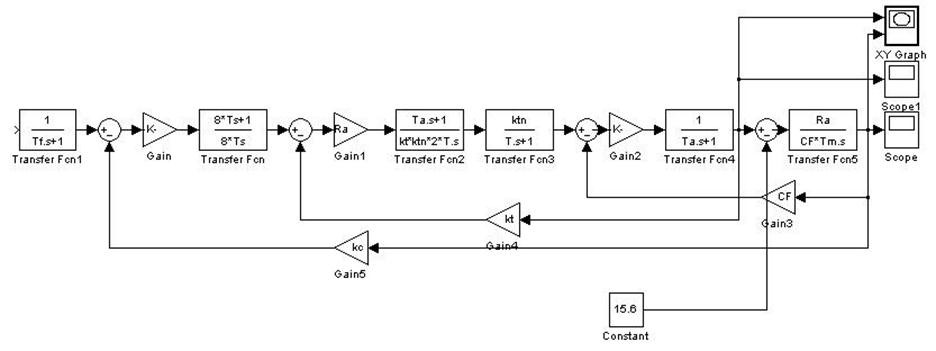
Рис. 15. Структурная схема для построения зависимостей , ,

Построим зависимости  и w(t)

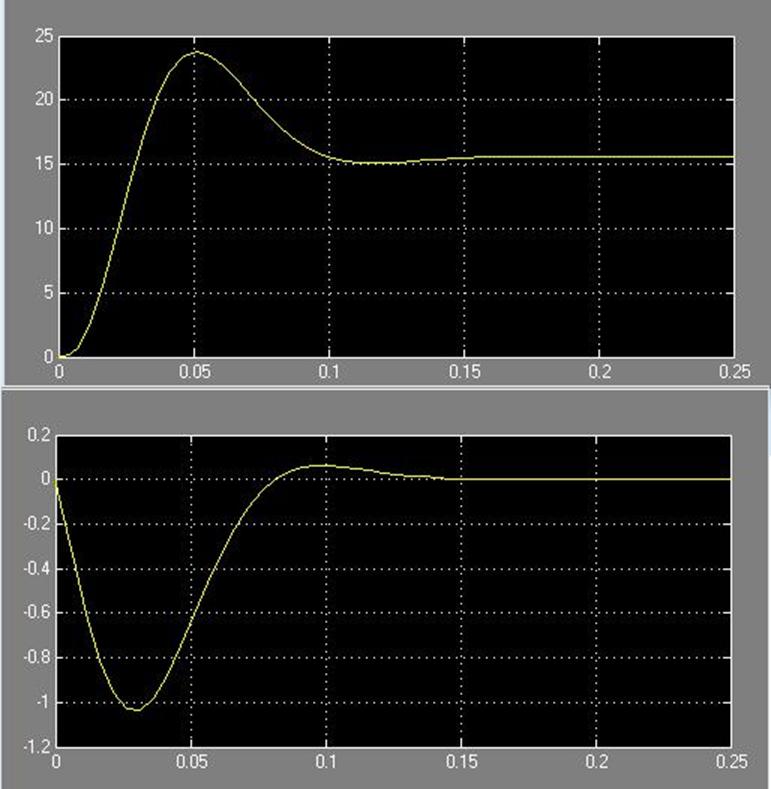
Рис 16. Зависимости  и w(t )соответственно

Построим зависимость

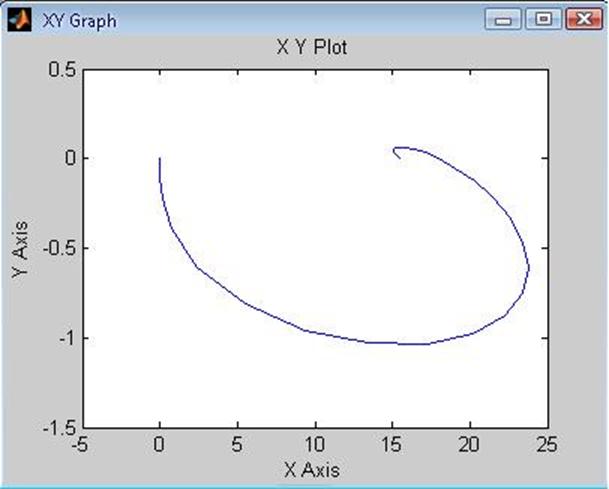
Рис.17. Динамическая электромеханическая характеристика

Определение установившейся ошибки

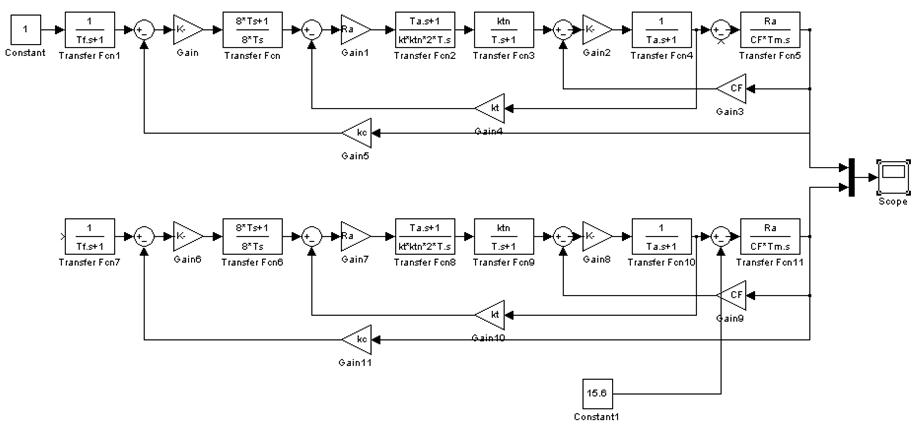
Рис.17.1 Структурная схема

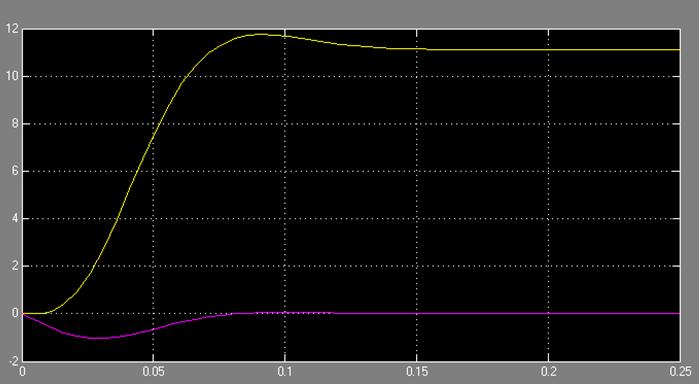
Рис.17.2 Характеристика

По отношению к сигналу нагрузки система астатична, следовательно, е_уст = 0.

8.4 Построение графиков изменения во времени угловой скорости вращения и тока якоря двигателя при подаче на вход САУ помехи и соответствующей электромеханической характеристики

Подадим на вход САУ помеху

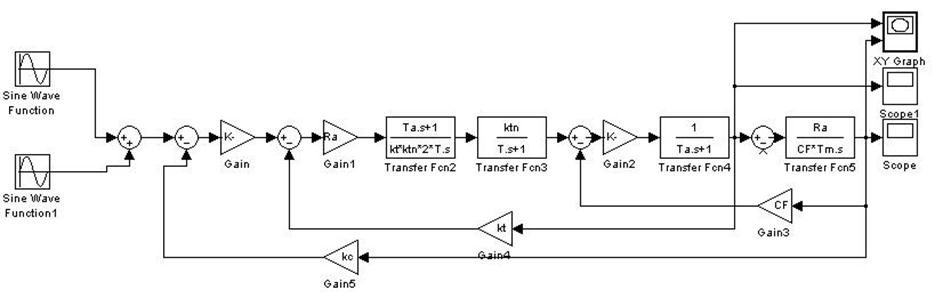
Рис. 18 Структурная схема для построения зависимостей , ,

Построим зависимости  и w(t)

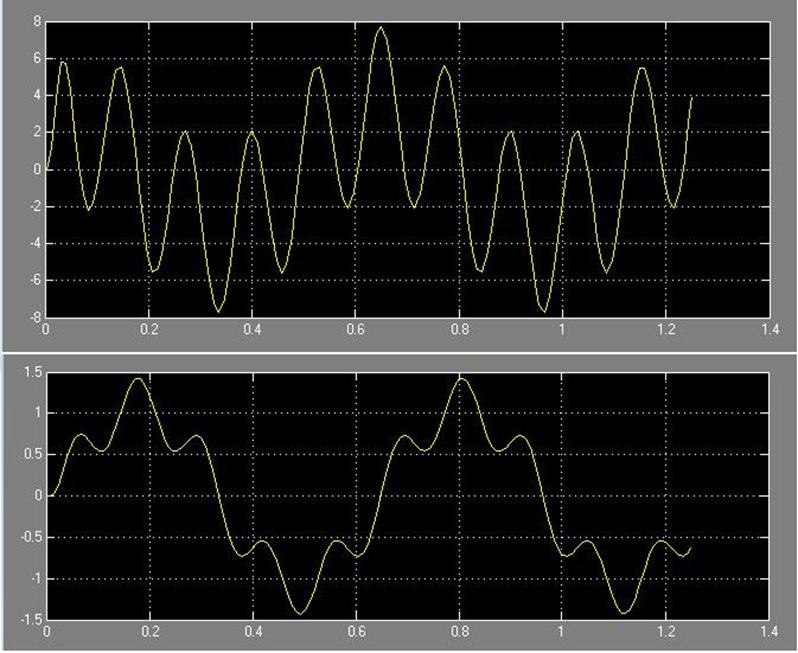
Рис. 19 Графики i(t) и w(t) соответственно с фильтром

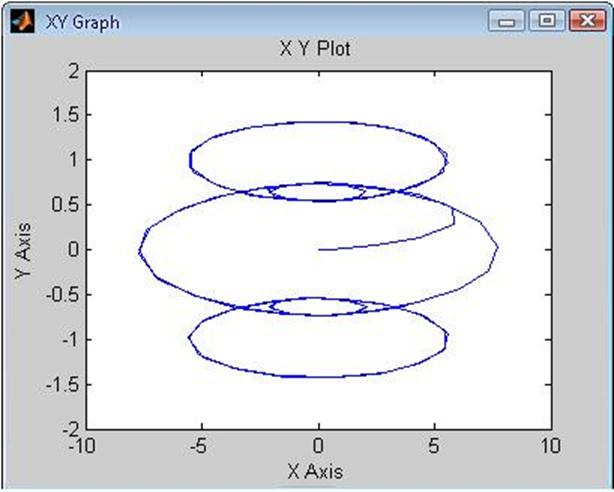
Рис. 20 Динамическая электромеханическая характеристика

8.5. Определение коэффициента передачи

• Численным методом

- амплитуда основной гармоники:

- амплитуда сигнала на выходе системы:

       Т.о. коэффициент передачи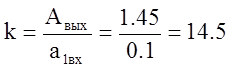           

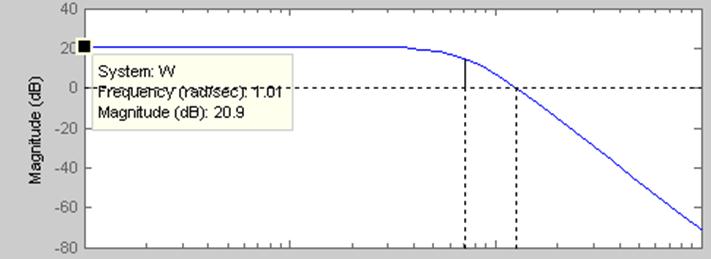
• По ЛАЧХ

Рис. 21 ЛАЧХ

По графику найдем L(w): , тогда коэффициент передачи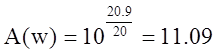  

9. Синтез цифрового регулятора скорости              

Реализация регулятора скорости в цифровой форме соответствует замене передаточной функции W_РС(р) в аналоговой системе передаточной функцией W_РС(Z).

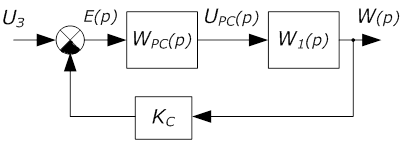
а)

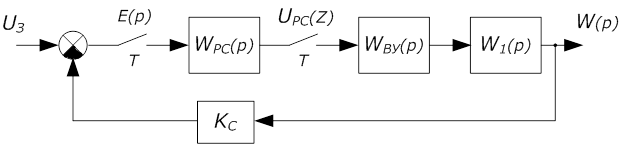
б)

Рис. 22. Структурные схемы систем регулирования скорости

(а) – аналоговый вариант, (б) – цифровой вариант

На рис. 22.

W₁(р) – передаточная функция подсистемы регулирования тока;

W_ВУ(р) – передаточная функция восстанавливающего устройства;

Т – период прерывания

Передаточная функция цифрового регулятора определяется по передаточной функции аналогового прототипа с применением:

– стандартного Z–преобразования, использование которого соответствует замене переменной р в соответствии с выражением

;

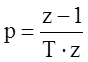– билинейного преобразования в соответствии с подстановкой

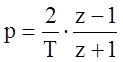
Каждый из способов проделываем для двух периодов прерывания:

Z-преобразование:

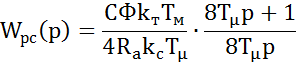
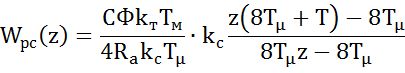
Билинейное преобразование:

,

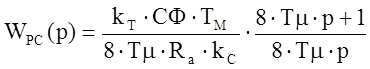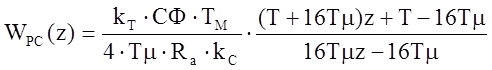
Для реализации восстанавливающего устройства нулевого порядка в MATLAB применяем блок Zero-Order Hold. Во всех дискретных блоках задаем период прерывания.

10. Анализ САУ с цифровым регулятором

10.1. Стандартные Z – преобразования

10.1.1. Найдем запасы устойчивости по амплитуде и по фазе

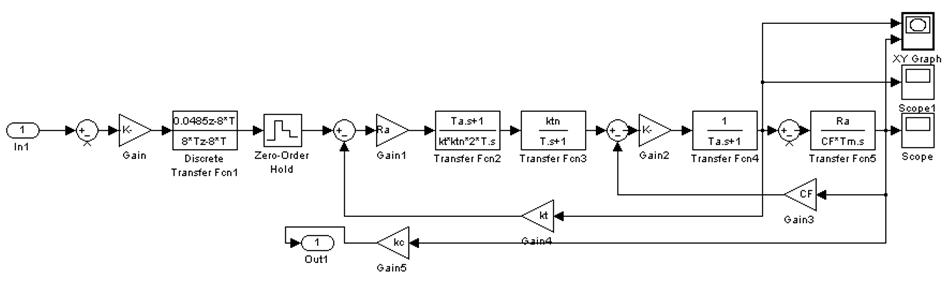
Рис. 23 Структурная схема для определения запасов

T=0.05*Ta

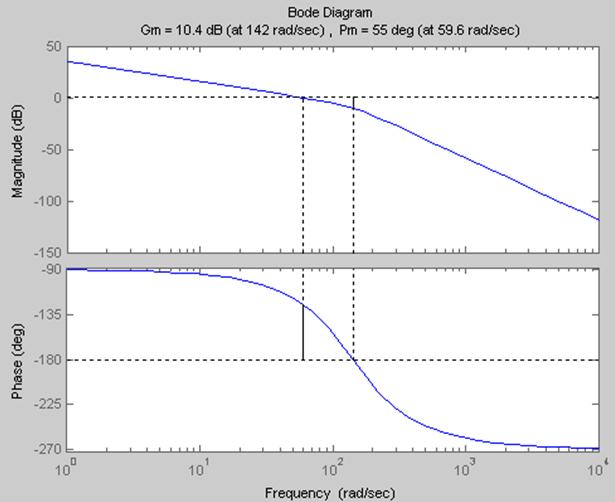
Рис. 24 Запасы устойчивости: ,   ;

 à система устойчива

T=0.5*Ta

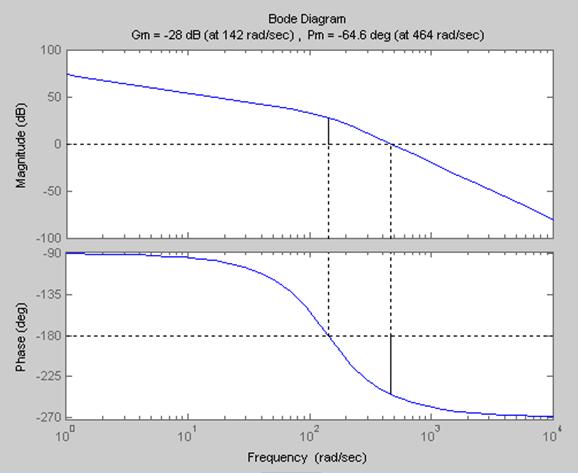
Рис. 25 Запасы:

 à система неустойчива

При  T=0.5*Ta система не устойчивая. Проделаем дальнейшие опыты, чтобы убедиться в этом.

10.1.2 Построение зависимостей , ,  при подаче на вход единичного ступенчатого сигнала

Построим зависимости  и i(t)

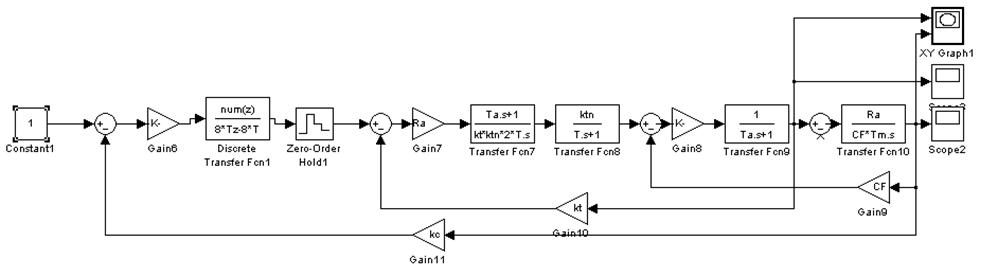
Рис. 26. Структурная схема для построения зависимостей ,  i(t) и w(i)

T = 0.05*Ta

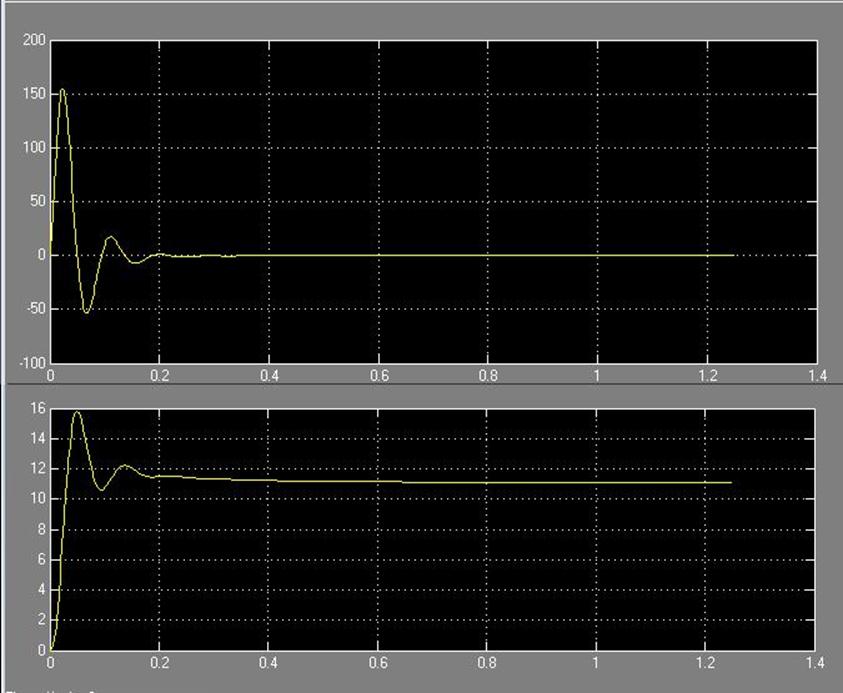
Рис. 27 Зависимость системы i(t) и w(t) с цифровым регулятором без фильтра

Из графика можно определить получившиеся показатели качества:

- перерегулирование: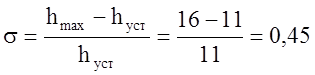  

 - время регулирования: 

T = 0,5*Ta

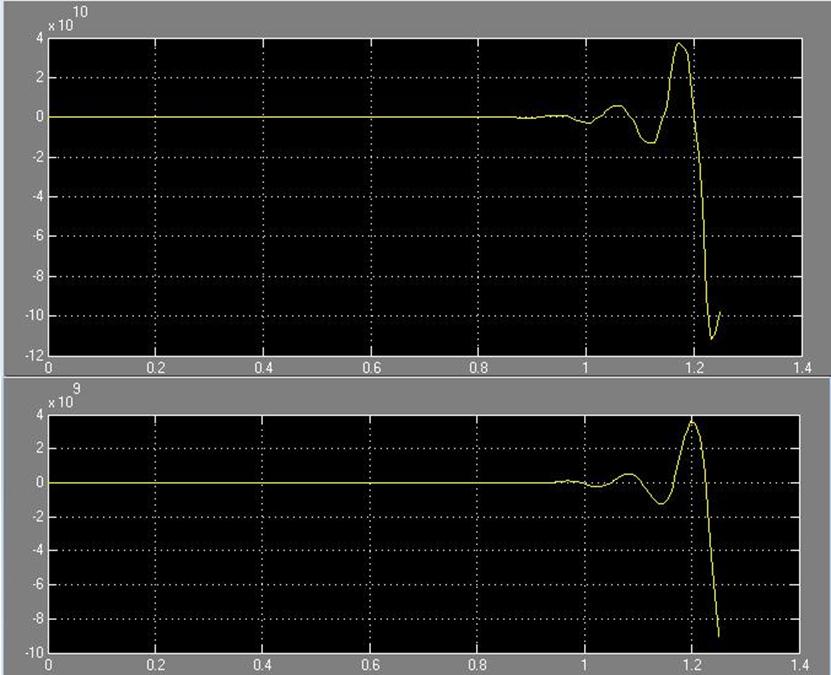
Рис. 28 Зависимость системы i(t) и w(t) с цифровым регулятором соответственно без фильтра

Процессы расходящиеся, следовательно, система неустойчива при T = 0,5*Ta.

     

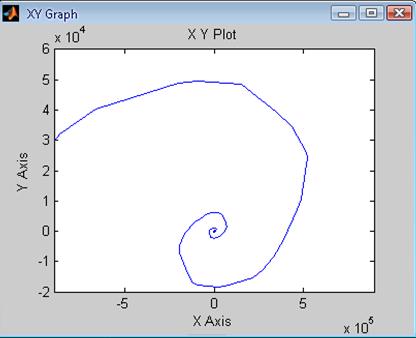
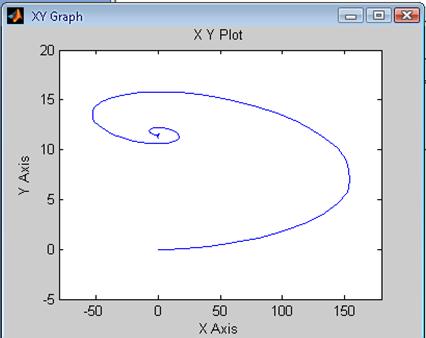
Рис. 29. Зависимость  системы с                    Рис. 30 Зависимость системы с

цифровым регулятором скорости                          цифровым регулятором скорости

 при T = 0.5*Ta  без фильтра                                       при T = 0.05*Ta без фильтра

T = 0.05*Ta

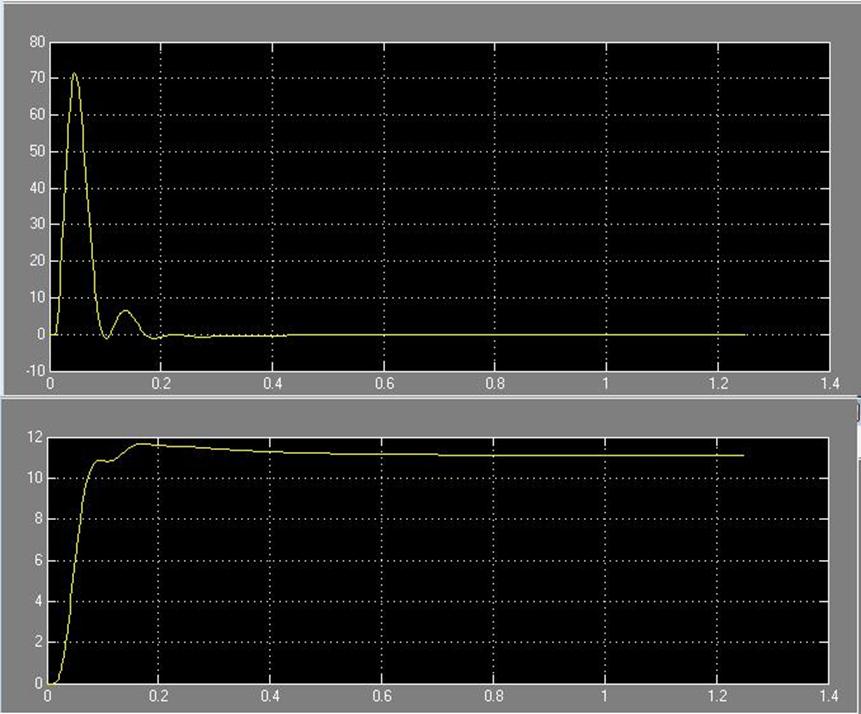
Рис. 31 Зависимость системы i(t) и w(t) с цифровым регулятором с фильтром соответственно

Из графика можно определить получившиеся показатели качества:

- перерегулирование: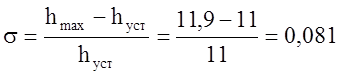   

- время регулирования:

T = 0,5*Ta

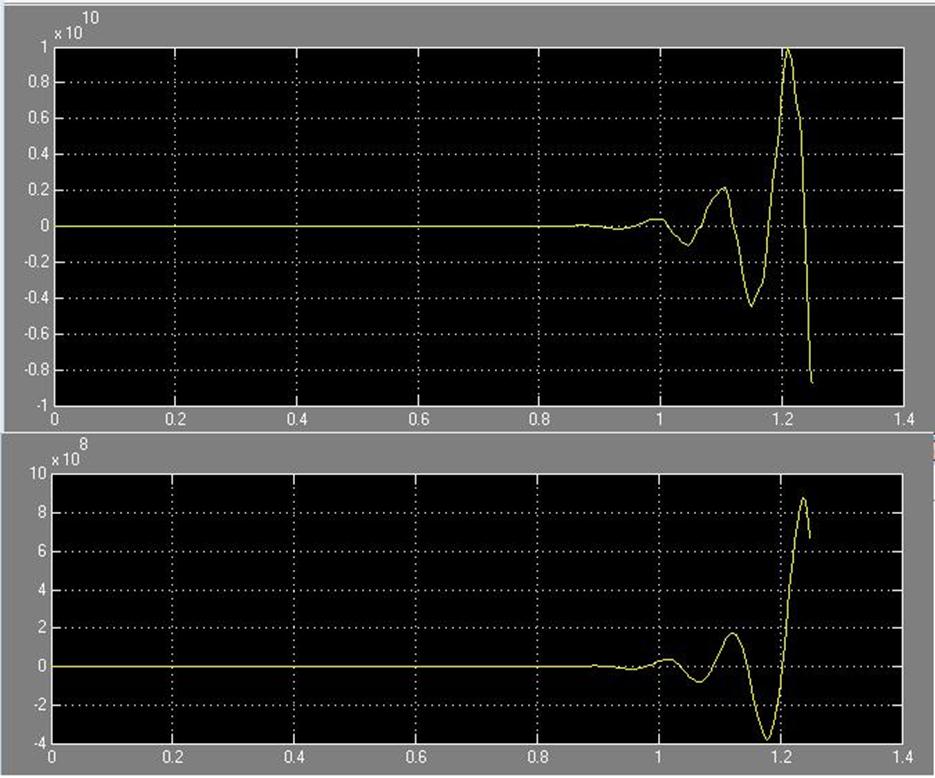
Рис. 32 Зависимость системы i(t) и w(t) с цифровым регулятором с фильтром соответственно

10.1.3. Построение зависимостей , ,  при ступенчатом приложении нагрузки

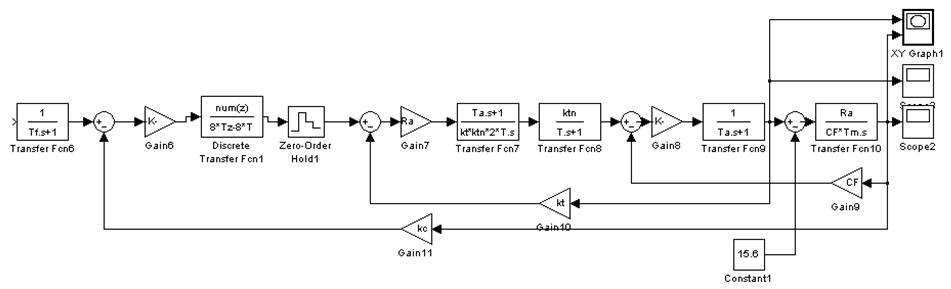
Рис. 33 Структурная схема для построения зависимостей , ,  с фильтром

T = 0.5*Ta

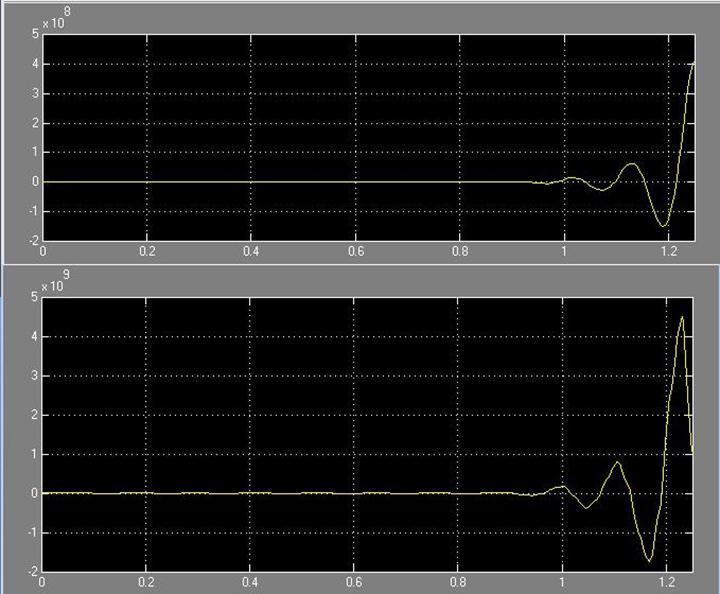
Рис. 34. Зависимость системы w(t) и i(t) с цифровым регулятором с фильтром при ступенчатом приложении  нагрузки

T = 0.05*Ta

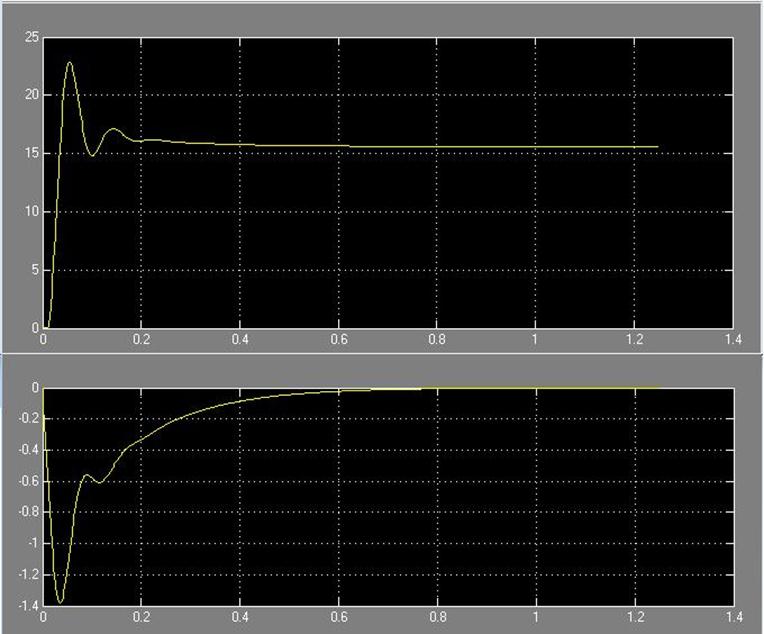
Рис. 35. Зависимость системы i(t) и w(t) с цифровым регулятором с фильтром

     

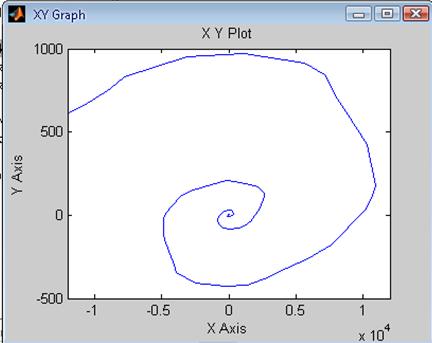
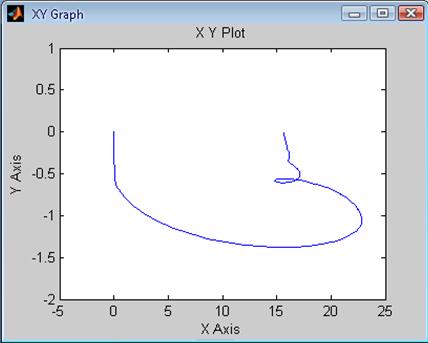
Рис. 36 Зависимость  системы с                    Рис. 37 Зависимость системы с

цифровым регулятором скорости                          цифровым регулятором скорости

 при T = 0.5*Ta  с фильтром                                       при T = 0.05*Ta с фильтром

Определение установившейся ошибки

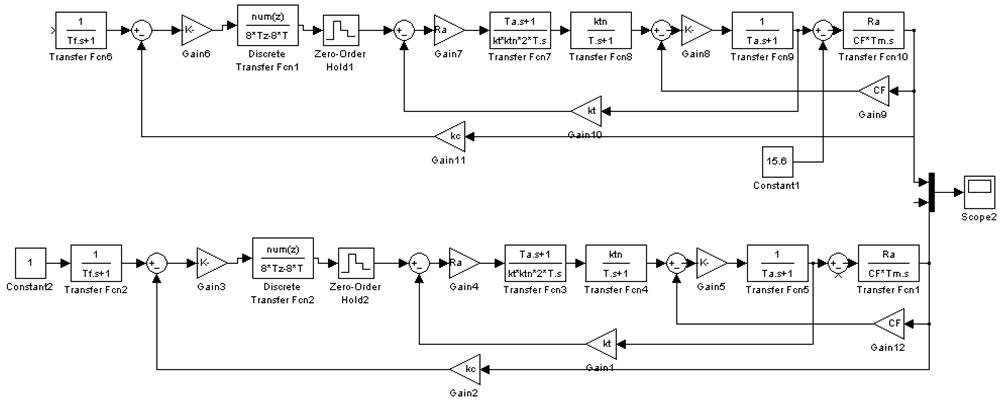
Рис. 37.1 Зависимость системы i(t) и w(t) с цифровым регулятором с фильтром

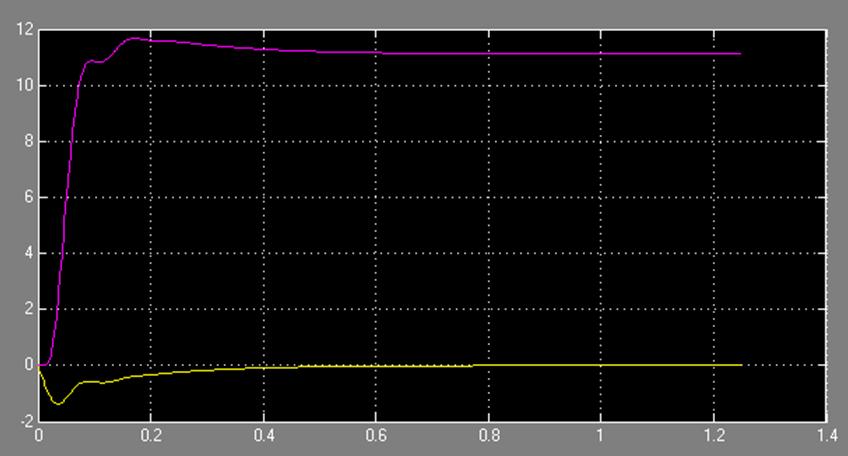
Рис. 37.2 Получившийся процесс

По отношению к сигналу нагрузки, так же как и с не цифровым регулятором скорости, система астатична, следовательно, е_уст = 0.

10.1.4. Построение зависимостей , ,  при подачи на вход помехи без фильтра