Предельное значение изображения (Анализ теоремы)

Предельное значение изображения

Теорема 12. Если решетчатая функция  является оригиналом и имеет изображение , то начальное значение решетчатой функции определяется по формуле:

  (1)

Где предел при  берется по любой кривой, которая принадлежит области определения , и удовлетворяет условию 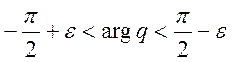, где  - сколь угодное малое положительное число.

Доказательство:

Представим основную формулу дискретного преобразования Лапласа:

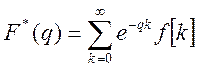
Вычислим начальное значение решетчатой функции:

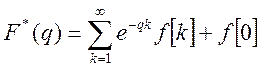  (2)

Так как решетчатая функция по условию теоремы является оригиналом, то должно выполняться неравенство:

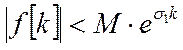
Где  - показатель роста решетчатой функции.

Тогда сумма правой части уравнения (2) допускает следующую оценку:

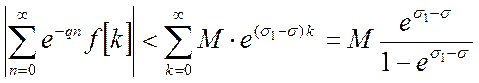  (3)

Если теперь , оставаясь внутри угла 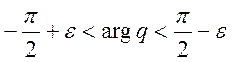, то .

Правая часть выражения (3) при этом стремится к нулю, и левая его часть также стремится к нулю.

Из уравнения (2) получаем следующее выражение:

Теорема доказана.