Построение частотных характеристик блоков структурной схемы

1. Построить все частотные характеристики блоков структурной схемы и принципиальные схемы моделирования блоков на операционных усилителях.

Построение частотных характеристик блоков структурной схемы.

Построим графики мнимой (Q(w)) и действительной (P(w)) части передаточной функции  W(jw), а также АЧХ А(w), ФЧХ j(w), ЛАЧХ L(w), ЛФЧХ F(w) и годограф Q(P).

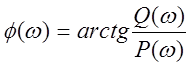
Рассмотрим первое звено:

КЧХ       

ВЧХ      

МЧХ     

AЧХ      

ФЧХ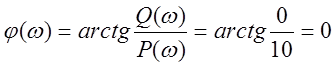       

ЛАЧХ      

ЛФЧХ       

ВЧХ	МЧХ	КЧХ(годограф)

АЧХ	ФЧХ	ЛАЧХ

Рассмотрим второе звено.

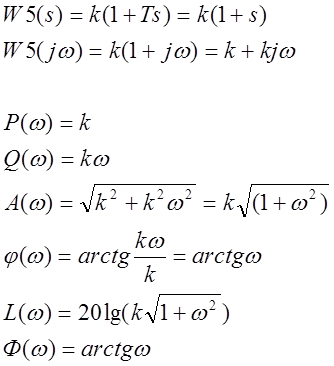
Строим графики частотных характеристик для  K1=1, K2=5, K3= - 2.

ВЧХ	МЧХ	АЧХ

КЧХ	ФЧХ	ЛАЧХ

Рассмотрим третье звено.

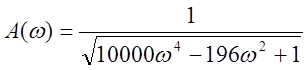
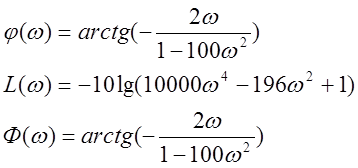
ВЧХ	МЧХ	АЧХ

КЧХ	ЛАЧХ	ФЧХ

Синтез схем блоков на операционных усилителях.

Рассмотрим первое звено:

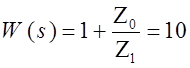
Выбираем сопротивления  и .

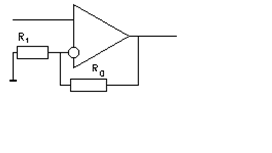Рассмотрим второе звено:

                                

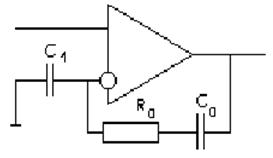
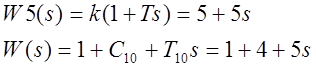
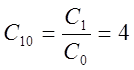
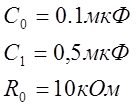
Рассмотрим третье звено:

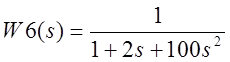
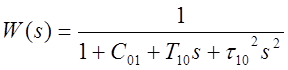
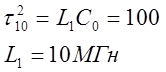
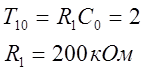
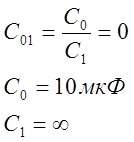
2. Получить ПФ Wр(s) разомкнутой системы.

Из рис. 1.1 находится соответствующая система уравнений .

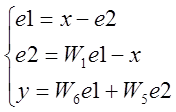
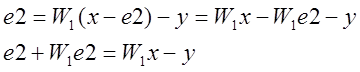
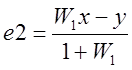
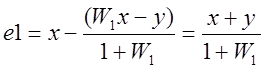
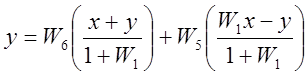
Преобразовав данное выражение получаем.

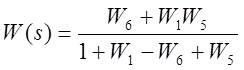
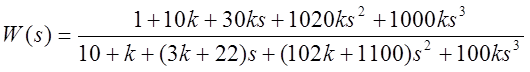
3.Исследовать устойчивость разомкнутой системы от буквенного параметра методами Гурвица и Михайлова.

.

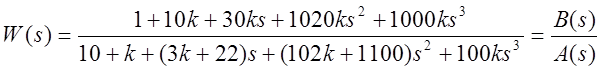
  3.1. Исследование устойчивости методом Гурвица.

Этот алгебраический критерий устойчивости работает с характеристическим полиномом (ХП) , который является полиномом знаменателя ПФ исследуемой системы. Для РС, у которого ПФ ,  .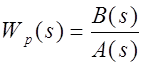

Коэффициенты характеристического полинома зависят от 2-х параметров: s,k.

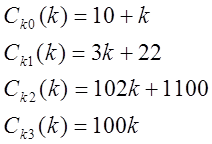
Условия устойчивости.

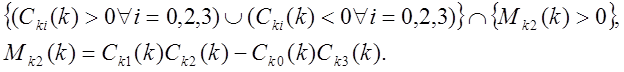
1)                         

                                            

Общее решение 

2)                            

                                              

Общее решение 

3)

 

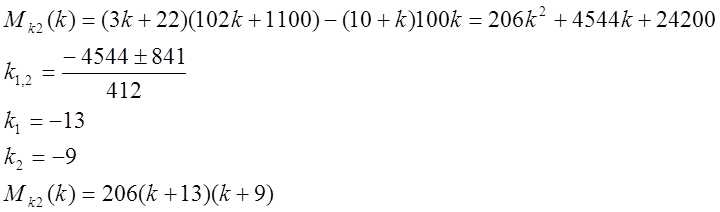
  при   и 

Объединяя все полученные решения , выяснили что разомкнутая система устойчива

при   и  .

  2. Исследование устойчивости методом Михайлова.

    Критерий устойчивости Михайлова:

для устойчивости линейной системы необходимо и достаточно, чтобы изменение аргумента годографа ее ХП степени n было определенным и составляло np/2 рад или n квадрантов при изменении частоты от 0 до ¥.

    Математическая формулировка критерия устойчивости Михайлова:

для устойчивости линейной системы необходимо и достаточно, чтобы коэффициенты С0 и С1 ее ХП С(s) были ненулевыми и одного знака, а корни  уравнений  и  чередовались по возрастанию в соответствии с выражением:          

Работаем с тем же ХП.

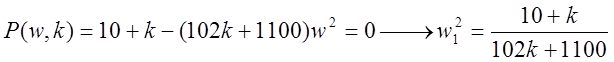
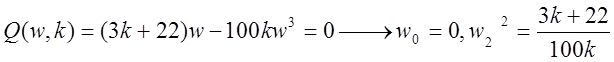
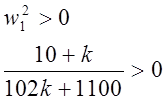
1)

                                              Получили  k<-10.78 и k>-10.

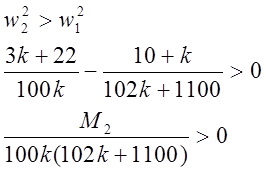2)

                                                                      Получили k<-13,  -10.78<k<-9 и k>0.

3)         Получили k<-10 и k>-7.14.

Объединяя ответы получаем, что разомкнутая система с ПФ  устойчива при:

4. Получить ПФ W_з(s) системы замкнутой единичной отрицательной обратной связью.

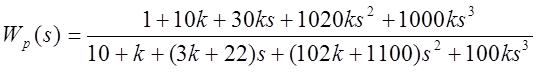
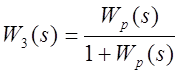
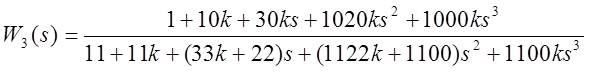
ХП:

5. Исследовать устойчивость замкнутой системы от буквенного параметра методами Гурвица и Рауса. Получить диапазоны устойчивых и неустойчивых значений параметра в классе вещественных чисел.

  Критерий Рауса-Гурвица:

Построим матрицу Гурвица:

      

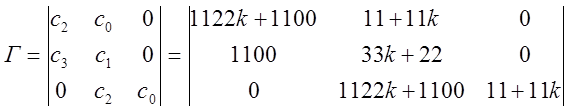
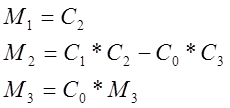
Для устойчивости действительного полинома необходимо и достаточно, чтобы все элементы последовательности  были одного знака, то есть 

   Если , то все главные миноры должны быть положительны. Если , то знаки миноров должны чередоваться , начиная с .

Работаем с ХП ПФ замкнутой системы:

Условие устойчивости:

1) 11+11k>0                  1122k+1100>0                 1100k>0

       k>-1                           k>-0.98                              k>0

     Получили k>0.

2) 11+11k<0                  1122k+1100<0                 1100k<0

       k<-1                           k<-0.98                              k<0

    Получили k<-1.

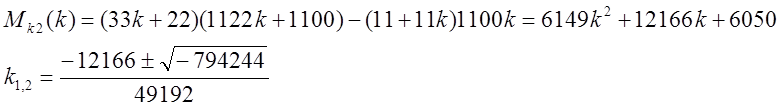3)

Коэффициенты полученного квадратного уравнения >0, значит ветви этой параболы направлены вверх. Она не имеет пересечений с осью k, следовательно k-любое число.

Объединяя ответы получим , что замкнутая система устойчива при k<-1 и k>0.

6. Cформировать набор значений параметра, включающий все граничные значения и по одному значению из каждого диапазона устойчивости и неустойчивости замкнутой системы.

Учитывая, что ЗС является устойчивой, когда  k<-1 и k>0, получим:

·  Значение, при которых система находится на границе устойчивости:  k= -1

·  Значения, при котором ЗС является устойчивой: k=5 и k= -10

·  Значение, при которых ЗС находится в неустойчивом состоянии: k= -0.1

7. Для каждого значения параметра из набора построить частотные характеристики, необходимые для исследования устойчивости замкнутой системы от параметра по критериям Найквиста и Михайлова.

Устойчивость ЗС по Михайлову определяется на основе годографа ХП     

Построим годографы Михайлова для замкнутой системы с единичной отрицательной ОС для значений k= -10; -1; -0.1, 5; . Подставим эти значения k в мнимую и действительную части ХП.

1) k= -10.

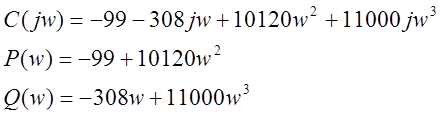
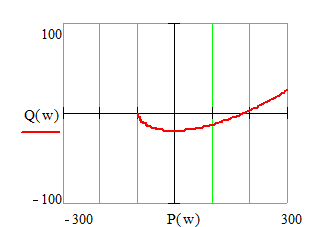
При данном k система устойчива т.к. годограф начинается на действительной оси и изменение аргумента годографа ее ХП третьей степени определенно и составляет Dk=3 квадранта, что соответствует числу правых корней 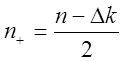=0.

2) k= -1

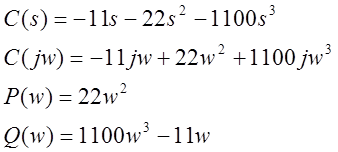
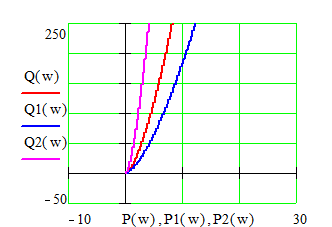
При k=-1 годограф выходит из начала координат, что означает, что  годограф находится на границе устойчивости. Строим годографы, изменяя k на малое значение вокруг точки k= -1. Берем k= -1.01 и k= -0.99.

Малые вариации параметра в окрестности точки k смещают годограф влево (неустойчивость) или вправо (устойчивость). Следовательно, при k= -1 система является нейтральной.

3) k= -0.1

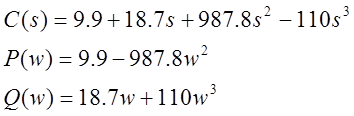
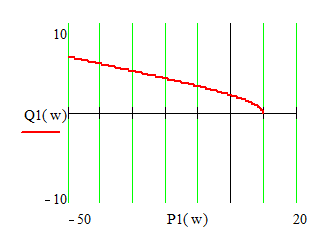
4) k= 5

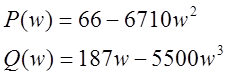
Логарифмический критерий Найквиста.

1)k= -10

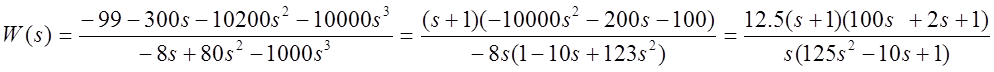
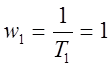      рад/c

 

     

  

 

  

  

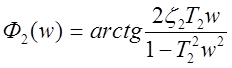
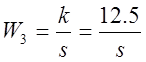
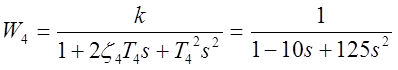
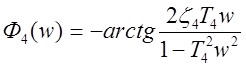
2)k= -1

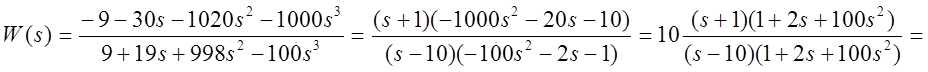
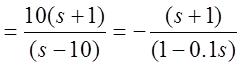
-(1+T₁s)= -(1+s)

T₁=1 1рад/с

 

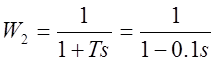
T₂= -0.1   рад/с

    

3)k= -0.1